Get my PhD Thesis

More documents

Recommendations

Info

L. Thøgersen, J. Olsen / Chemical Physics Letters 393 (2004) 36–43 39 From the above comparisons, it may be concluded, that the open-shell nature of CN does not lead to slower convergence of the CC hierarchy than previously observed for N 2 . However, it should be noted, that the convergence of the CC hierarchy for N 2 is rather slow compared to the convergence observed for e.g., H 2 O [19] and F 2 . 3.2. The potential curve for CN FCI calculations were carried out at a number of internuclear distances. To obtain accurate spectroscopic constants, the CC energies were converged to 10 9 E h Table 2 FCI energies (E h ) as a function of internuclear distance ( A) for CN using the cc-pVDZ basis R E R E 0.9 )92.169732 1.2118 )92.494065103 1.0 )92.384032 1.2169 )92.493765608 1.0918 )92.469313943 1.2369 )92.491837833 1.1318 )92.485677652 1.2518 )92.489691918 1.1518 )92.490432414 1.30 )92.479361 1.1569 )92.491327096 1.40 )92.447147 1.1718 )92.493262415 1.50 )92.408657 1.1769 )92.493704946 1.60 )92.370048 1.1869 )92.494267979 1.7577 )92.316388 1.1918 )92.494402963 2.05065 )92.255688 1.1919 )92.494404785 2.3436 )92.241450 1.1969 )92.494449358 2.9295 )92.240346 1.2019 )92.494404774 3.5154 )92.239697 1.2069 )92.494274026 for internuclear distances close to the experimental value. For the remaining geometries the energy was converged to 10 6 E h . The obtained FCI energies are listed in Table 2. The graph of the FCI potential curve is given in Fig. 2. To associate the various internuclear distances with a degree of bond-breaking it is useful to examine the coefficient of the Hartree–Fock determinant in the FCI wave-function. Around the equilibrium geometry, the weight of the HF-determinant is about 0.92. Increasing the internuclear distance leads to a steady lowering of this weight and at 1.3 and 1.8 A, the weights are 0.79 and 0.57, respectively. From 1.8 to 2.0 A the weight drops sharply so the weight at 2.0 A is 0.25 and at 2.5 A less than 0.04. We may therefore say that the bond is half broken at 1.8 A and broken at 2.5 A. In addition to FCI calculations, CCSD(orb), CCSDT(orb) and CCSDTQ(orb) calculations were performed at the various internuclear distances up to 1.8 A. Although it is possible to converge the CC equations for larger distances, we find this of less interest, due to the breakdown of the single-reference approximation. In Fig. 3, we plot the deviations of the CCSDT and CCSDTQ energies from the FCI energy, and in Table 3, we list the non-parallelity error (NPE), i.e., the difference between the largest and smallest deviation from the FCI energy. At the equilibrium distance, both deviation curves in Fig. 3 have a positive curvature. For internuclear distances larger than the equilibrium distance, both the CCSDT and CCSDTQ deviation curves are nearly -92.15 -92.20 -92.25 FCI energy -92.30 -92.35 -92.40 -92.45 -92.50 0.5 1 1.5 2 2.5 3 3.5 4 Internuclear distance Fig. 2. The FCI potential curve for CN using the cc-pVDZ basis. The energies are in Hartrees and the inter-nuclear distances are in A.
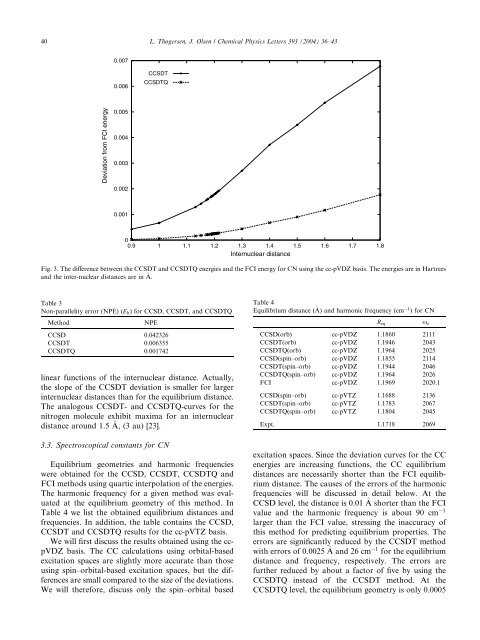
40 L. Thøgersen, J. Olsen / Chemical Physics Letters 393 (2004) 36–43 0.007 0.006 CCSDT CCSDTQ Deviation from FCI energy 0.005 0.004 0.003 0.002 0.001 0 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 Internuclear distance Fig. 3. The difference between the CCSDT and CCSDTQ energies and the FCI energy for CN using the cc-pVDZ basis. The energies are in Hartrees and the inter-nuclear distances are in A. Table 3 Non-parallelity error (NPE) (E h ) for CCSD, CCSDT, and CCSDTQ Method NPE CCSD 0.042326 CCSDT 0.006355 CCSDTQ 0.001742 linear functions of the internuclear distance. Actually, the slope of the CCSDT deviation is smaller for larger internuclear distances than for the equilibrium distance. The analogous CCSDT- and CCSDTQ-curves for the nitrogen molecule exhibit maxima for an internuclear distance around 1.5 A, (3 au) [23]. 3.3. Spectroscopical constants for CN Equilibrium geometries and harmonic frequencies were obtained for the CCSD, CCSDT, CCSDTQ and FCI methods using quartic interpolation of the energies. The harmonic frequency for a given method was evaluated at the equilibrium geometry of this method. In Table 4 we list the obtained equilibrium distances and frequencies. In addition, the table contains the CCSD, CCSDT and CCSDTQ results for the cc-pVTZ basis. We will first discuss the results obtained using the ccpVDZ basis. The CC calculations using orbital-based excitation spaces are slightly more accurate than those using spin–orbital-based excitation spaces, but the differences are small compared to the size of the deviations. We will therefore, discuss only the spin–orbital based Table 4 Equilibrium distance ( A) and harmonic frequency (cm 1 ) for CN CCSD(orb) cc-pVDZ 1.1860 2111 CCSDT(orb) cc-pVDZ 1.1946 2043 CCSDTQ(orb) cc-pVDZ 1.1964 2025 CCSD(spin–orb) cc-pVDZ 1.1855 2114 CCSDT(spin–orb) cc-pVDZ 1.1944 2046 CCSDTQ(spin–orb) cc-pVDZ 1.1964 2026 FCI cc-pVDZ 1.1969 2020.1 CCSD(spin–orb) cc-pVTZ 1.1688 2136 CCSDT(spin–orb) cc-pVTZ 1.1783 2067 CCSDTQ(spin–orb) cc-pVTZ 1.1804 2045 Expt. 1.1718 2069 excitation spaces. Since the deviation curves for the CC energies are increasing functions, the CC equilibrium distances are necessarily shorter than the FCI equilibrium distance. The causes of the errors of the harmonic frequencies will be discussed in detail below. At the CCSD level, the distance is 0.01 A shorter than the FCI value and the harmonic frequency is about 90 cm 1 larger than the FCI value, stressing the inaccuracy of this method for predicting equilibrium properties. The errors are significantly reduced by the CCSDT method with errors of 0.0025 A and 26 cm 1 for the equilibrium distance and frequency, respectively. The errors are further reduced by about a factor of five by using the CCSDTQ instead of the CCSDT method. At the CCSDTQ level, the equilibrium geometry is only 0.0005 R eq x e
Page 1:
PhD Thesis Optimization of Densitie
Page 5 and 6:
Contents Preface ..................
Page 7:
Summary............................
Page 11:
List of Publications This thesis in
Page 14 and 15:
Part 1 Improving Self-consistent Fi
Page 16 and 17:
Page 18 and 19:
Page 20 and 21:
Page 22 and 23:
Page 24 and 25:
Page 26 and 27:
Page 28 and 29:
Page 30 and 31:
Page 32 and 33:
Page 34 and 35:
Page 36 and 37:
Page 38 and 39:
Page 40 and 41:
Page 42 and 43:
Page 44 and 45:
Page 46 and 47:
Page 48 and 49:
Page 50 and 51:
Page 52 and 53:
Page 54 and 55:
Page 56 and 57:
Page 58 and 59:
Page 60 and 61:
Page 62 and 63:
Page 64 and 65:
Page 66 and 67:
Page 68 and 69:
Page 70 and 71:
Page 72 and 73:
Part 2 Atomic Orbital Based Respons
Page 74 and 75:
Page 76 and 77:
Page 78 and 79:
Page 80 and 81:
Page 82 and 83:
Page 84 and 85:
Page 86 and 87:
Page 88 and 89:
Page 90 and 91:
Part 3 Benchmarking for Radicals ar
Page 92 and 93:
Part 3 Benchmarking for Radicals le
Page 94 and 95:
Part 3 Benchmarking for Radicals As
Page 96 and 97:
Part 3 Benchmarking for Radicals R
Page 99:
Summary The developments in compute
Page 103: Appendix A The Derivatives of the D
Page 106 and 107: Thus, the density element D µν is
Page 109 and 110: References 1 2 3 4 5 6 7 8 9 C. C.
Page 111: 65 T. Helgaker and P. Jørgensen, T
Page 115 and 116: JOURNAL OF CHEMICAL PHYSICS VOLUME
Page 117 and 118: 18 J. Chem. Phys., Vol. 121, No. 1,
Page 127: Part 1 The Trust-region Self-consis
Page 130 and 131: 074103-2 Thøgersen et al. J. Chem.
Page 138 and 139: 074103-10 Thøgersen et al. J. Chem
Page 147: Part 3 A Coupled Cluster and Full C
Page 150 and 151: L. Thøgersen, J. Olsen / Chemical
Page 159 and 160: 3030 J. Phys. Chem. A 2004, 108, 30
Page 161 and 162: 3032 J. Phys. Chem. A, Vol. 108, No
Page 163: 3034 J. Phys. Chem. A, Vol. 108, No
show all

Get my PhD Thesis

Create successful ePaper yourself

Delete template?

Save as template?