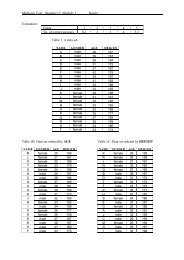
Slide 1 First-order Logic

Kabos: IntroLogic slides 25 Oct 2007
✬
✩
Slide 1
First-order Logic
✫
✬
✪
✩
Predicates and Quantifiers
Slide 2
Predicate logic generalizes the grammatical predicate
and relations.
Result of applying a predicate P to an object x is the
proposition P(x).
✫
✬
✪
✩
Slide 3
Quantifiers provide a formal notation that allow us
to quantify how many objects in the universe set
satisfy a given predicate.
✫
✪

Kabos: IntroLogic slides 25 Oct 2007
✬
✩
Slide 4
U: all animals
A(x): x is an alligator
R(x): x is a reptile
Z(x): x lives at the Zoo.
Some reptile lives at the zoo.
∃x (R(x) & Z(x))
✫
✬
✪
✩
Slide 5
U: all animals
A(x): x is an alligator
R(x): x is a reptile
Z(x): x lives at the Zoo.
Every alligator is a reptile.
∀x (A(x) → R(x))
✫
✬
✪
✩
Slide 6
U: all animals
A(x): x is an alligator
R(x): x is a reptile
Z(x): x lives at the Zoo.
There are reptiles which are
not alligators.
∃x (R(x) & ¬A(x)) ⇐⇒ ¬(∀x (R(x) → A(x)))
✫
✪

Kabos: IntroLogic First-order theories / 1
First-order theories
Propositional calculus
Syntax
Variable (in Propositional Calculus):
an element of the Universe set {T, F }
List of symbols:
1. variables: A, B, C,...
2. logical constants T, F
3. logical operators: ¬, &, ∨, →, ↔, ...
4. parentheses ( left , right)
Formula: is defined recursively by the rules
1. variable or constant
2. if ϕ is a formula then ¬ϕ is a formula
3. if ϕ and ψ are formulae then ϕ → ψ is a formula
4. nothing else is a formula
Logical axioms:
A1: ϕ → (ψ → ϕ)
A2: (ϕ → (ψ → ρ)) → ((ϕ → ψ) → (ϕ → ρ))
A3: (¬ϕ → ψ) → ((¬ϕ → ¬ψ) → ϕ)
Inference rule Modus Ponens (MP):
if ϕ → ψ and ϕ then ψ
Let S be a set of formulae.
Proof (=formal derivation) of a formula ϕ in S is a sequence
{ϕ 1 , ϕ 2 , ϕ 3 , ϕ 4 , ...ϕ i , ...ϕ} if every ϕ i is either elements of S, or a logical
axiom, or is made from two previous ϕ’s by inference rule Modus Ponens.
S ⊢ ϕ means that ϕ is provable (has a formal derivation in S).
Closure of S : set of all provable formulae in S.

Kabos: IntroLogic First-order theories / 2
Semantics
Interpretation of a formula: substituting values into variables.
A variable takes an element from the universe, and the interpreted formula
takes either T or F
Model of S : an interpretation when all formulae in S are T
S |= ϕ means that ϕ is entailed by S, that is ϕ takes T in every possible
model of S
Soundness: if S ⊢ ϕ then S |= ϕ
Completeness: if S |= ϕ then S ⊢ ϕ
It can be seen, that Propositional Logic is sound and complete.
First-order Calculus
Individual variable: (in First-order Calculus)
an element of a given Universe set U.
List of symbols:
1. individual variables: x, y, z , ...
2. constants: c,...
3. predicate variables (relations): P, Q, R ...
4. functions: f, g
5. quantifiers, universal: ∀ , existential: ∃
6. logical operators: ¬, &, ∨, →, ↔, ...
7. parentheses ( left , right)
Term: is defined recursively by the rules
1. individual variables and constants are terms,
2. if t 1 , .., t N are terms and f is a function then f(t 1 , t 2 , ..., t N ) is a term,
3. nothing else is a term.
Atomic formula:
If P is a predicate variable andt 1 , t 2 , ..., t N are terms, then P (t 1 , t 2 , ..., t N )
is an atomic formula

Kabos: IntroLogic First-order theories / 3
Formula: is defined recursively by the rules
1. an atomic formula,
2. if ϕ is a formula then ¬ϕ is a formula,
3. if ϕ és ψ are formulae then ϕ → ψ is a formula,
4. if ϕ a formula and x is a variable, then ∀xϕ is formula,
5. nothing else is a formula.
Free and bounded variables:
1. If ϕ is an atomic formula then x is free in ϕ if x occurs in ϕ
2. x is free in ¬ϕ if x is free in ϕ
3. x is free in (ϕ → ϕ) if x is free in ϕ and does not occur in ψ, or x is free
in ψ and does not occur in ϕ, or x is free in both ϕ and ψ
4. x is free in ∀y ϕ if x is free in ϕ and x is a different symbol than y
5. x is bound in ϕ if x occurs in ϕ and x is not free in ϕ
Rules of substitution variables in formulae, valid and invalid substitutions
(omitted here).
Conventions for equality (omitted here).
Logical axioms:
A1-A3 from propositional logic and
A4. omitted, it uses the concept of valid substitutions
A5. (∀x (ϕ → ψ)) −→ (ϕ → ∀x ψ) provided x is not a free variable in ϕ
Sentence:
Theory:
a formula without free variables
a set of sentences S
Proof (=formal derivation) of formula ϕ from S is the same as in
Propositional Calculus but we have an inference rule Universal
Generalisation (in addition to Modus Ponens)
Universal Generalisation:
if S ⊢ ϕ then S ⊢ ∀x ϕ
Closure of S : set of all provable sentences in S
Consistency of S : if ϕ is provable then and ¬ϕ is not.
Completeness of S : if ϕ is not provable then ¬ϕ is provable.
(to be continued)