Sistemas Hamiltonianos y Gradiente. Método analítico para la ...

3.1. SISTEMAS HAMILTONIANOS 13.1 Sistemas HamiltonianosEste tipo de sistemas aparecen frecuentemente en problemas físicos, y son fuente de numerososejemplos de aplicación de la teoría.Definición 3.1 Sea E un subconjunto abierto de R 2n yseaH ∈ C 2 (E), dondeH = H(x, y) conx, y ∈ R n . Unsistemadelaformaẋ = ∂H∂y ,ẏ = − ∂H(3.1)∂x ,conµ∂H ∂Hy∂y = , ..., ∂H t,∂y 1 ∂y nse denomina sistema Hamiltoniano con n grados de libertad en E. 4µ∂H ∂H∂x = , ..., ∂H t∂x 1 ∂x nEjemplo 3.1 Péndulo esféricoLa función Hamiltonianaes la función energía del péndulo esféricoH(x, y) = 1 2 (x2 1 + x 2 2 + y 2 1 + y 2 2)ẋ 1 = y 1 ,ẋ 2 = y 2,ẏ 1 = −x 1 ,ẏ 2 = −x 2,Este sistema es equivalente al par de osciladores armónicos desacopladosẍ 1 + x 1 = 0,ẍ 2 + x 2 = 0. 2Todos los sistemas Hamiltonianos son conservativos: la función Hamiltoniana o la energía totalpermanece constante a lo largo de las trayectorias del sistema.Teorema 1 (Conservación de la energía) La energía total H(x, y) del sistema Hamiltoniano(3.1) permanece constante a lo largo de las trayectorias de (3.1). 2Prueba: La derivada total de la función Hamiltoniana H(x, y) a lo largo de las trayectoria[x(t), y(t)] del sistema (3.1) esdHdt= ∂H∂x ẋ + ∂H∂y ẏ= ∂H∂x∂H∂y + ∂H∂yµ− ∂H =0.∂xPor lo tanto H(x, y) es constante sobre cualquier curva solución de (3.1), y las trayectorias de (3.1)yacen sobre las superficies H(x, y) =constante.Los sistemas Hamiltonianos de 1 grado de libertad son sistemas planares, y en este caso se puedenestablecer resultados muy específicos acerca de los puntos críticos o de equilibrio. Los puntosde equilibrio del sistema Hamitoniano (3.1) corresponden a los extremos relativos de la funciónH(x, y) donde ∂H/∂x = ∂H/∂y =0. En lo que sigue se supone sin pérdida de generalidad que elpuntodeequilibriobajoestudiohasidotrasladadoalorigen.

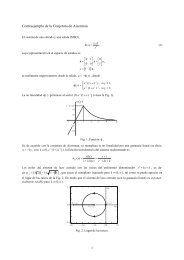
4que puede escribirse como el sistema Newtonianoẋ = y,ẏ = − sen x,donde (x, y) ∈ S 1 × R. El sistema tiene puntos de equilibrio en (0, 0) yen(±π, 0), y es sencillo determinarque el (0, 0) es un centro (los autovalores de la matriz jacobiana son imaginarios puros), y los puntos (±π, 0)son sillas. Usualmente el plano de fase suele graficarse como un cilindro, de modo que (±π, 0) es en realidadel mismo punto [Fig. 3.1(a)]. La función Hamiltoniana para este sistema es H(x, y) =T (y)+V (x) dondeT (y) = 1 2 y2 , y V (x) =Z x0−(− sen σ) dσ =1− cos x.La Fig. 3.1(b) muestra el gráfico de V (x) ylaFig.3.1(a) las trayectorias en el plano de fase del sistema,que se deducen de V (x) a partir del Teorema 3. La función H(x, y) y la proyección de diferentes curvas denivel sobre el plano x-y se grafica en la Fig. 3.2. El origen del plano de fase corresponde a la posición deequilibrio estable del péndulo colgando hacia abajo, y los puntos críticos en (±π, 0) correspondealaposiciónde equilibrio inestable del péndulo en posición invertida. Las trayectorias cerca del origen son elipses casiperfectas, y pueden ser aproximadas por las curvas solución del péndulo linealẍ + x =0.Las trayectorias cerradas que rodean al origen representan las movimientos periódicos del péndulo cuandooscila. Las trayectorias que conectan las sillas en (±π, 0) se denominan separatrices, y corresponden amovimientos con energía total H(x, y) =2en las cuales el péndulo se aproxima a la posición verticalinestable cuando t → ±∞. Lastrayectoriasfueradelasseparatrices(H(x, y) > 2) corresponden a rotacionespuras del péndulo, en uno u otro sentido. 2Ejemplo 3.3 Oscilador de Duffing sin amortiguamientoEste sistema se describe por la ecuación diferencialo por el sistema de ecuaciones de estadoẍ − x − δẋ + x 3 =0,ẋ = y,ẏ = x − x 3 − δy,donde (x, y) ∈ R 1 × R 1 , y δ ≥ 0 es el coeficiente de fricción. El sistema tiene tres puntos de equilibrio:en (0, 0) yen(±1, 0). La estructura local del plano de fase en cercanías del (0, 0) es la de una silla, y enentornos de (±1, 0) sonfocosestables. Enelcasoparticularenqueδ =0(amortiguamiento nulo) se puedecomprender la estructura global del plano de estados. En este caso el oscilador de Duffing es un sistemaconservativo, y por lo tanto su función energía es constante sobre las órbitas. La función Hamiltoniana esH(x, y) =T (y)+V (x) dondeZ xT (y) = 1 2 y2 , y V (x) = −(σ − σ 3 ) dσ = − x202 + x44 .Las curvas de nivel de H(x, y) dan la estructura global del plano de fase (Fig. 3.3). Nuevamente, estaestructura también puede derivarse a partir del gráfico de la función V (x) con la ayuda del Teorema 3,como se muestra en la Fig. 3.4. 2La función Hamiltoniana también se denomina primera integral del sistema. Se dice que el osciladorde Duffing del Ejemplo 3.3, con δ =0, es integrable, ya que al multiplicar la ecuación diferencialpor ẋẋẍ − ẋx + ẋx 3 =0,se tiene queµ d 1 2ẋ2 − x2dt 2 + x4=04que implica2ẋ2 1− x22 + x44 = h = constante.Esta función es una primera integral para el sistema de Duffing sin amortiguamiento, y coincidecon la expresión H(x, y) =h.

3.1. SISTEMAS HAMILTONIANOS 5Fig. 3.1: Trayectorias en S 1 × R (a) , función potencial V (x) (b) , y trayectorias en el plano de estado (c)del péndulo sin amortiguamiento.H(x, y)xyFig. 3.2: Función Hamiltoniana del péndulo sin amortiguamiento y la proyección de distintas curvas denivel sobre el plano x-y.

6H(x, y)xyFig. 3.3: Función Hamiltoniana del oscilador de Duffing y la proyección de distintas curvas de nivel sobreel plano x-y.Fig. 3.4: Función potencial V (x) (a) y trayectorias en el plano de estado (b) del oscilador de Duffing.

3.2. SISTEMAS GRADIENTE 9el plano de fase, la integral de líneaIΓẋdx+ ẏdy6= 0 (3.7)porque el campo vectorial es tangente a la curva Γ en todo punto. Sin embargo, para el sistemagradiente (3.5) se tiene queẋdx + ẏdy = − ∂V ∂Vdx −∂x ∂y dy.Cuando la expresión de la derecha se integra de a =(x 1 ,y 1 ) hasta b =(x 2 ,y 2 ) se obtieneZ ba− ∂V ∂Vdx −∂x ∂y dy = −V (x 2,y 2 )+V (x 1 ,y 1 )y por lo tanto, la integral sobre una curva cerrada (con a = b) es nula, que contradice (3.7).El mismo tipo de análisis permite demostrar que un sistema gradiente no puede tener un comportamientotipo foco o centro en un entorno de un punto de equilibrio no degenerado. En la Fig. 3.7se muestra la distribución de los sistemas Hamiltonianos y los sistemas gradiente en el espacio deparámetros ∆-τ de la matriz jacobiana.A pesar de estas diferencias, los sistemas Hamiltonianos y gradientes guardan entre sí una interesanterelación.Definición 3.4 Dado el sistema planarẋ = P (x, y),ẏ = Q(x, y),(3.8)el sistemaẋ = Q(x, y),ẏ = −P (x, y).(3.9)se denomina sistema ortogonal al sistema (3.8). 4Los sistemas (3.8) y (3.9) tienen los mismos puntos de equilibrio y los mismos puntos regulares,y las trayectorias de (3.8) son ortogonales a las de (3.9). Los centros de (3.8) corresponden anodos de (3.9), y ambos sistemas tienen las mismas sillas y focos. Además, si (3.8) es un sistemaHamiltoniano, con P = ∂H/∂y, Q = −∂H/∂x, entonces (3.9) es un sistema gradiente, y viceversa.Teorema 6 El sistema (3.8) es un sistema Hamiltoniano si y sólo si el sistema (3.9), ortogonal a(3.8), es un sistema gradiente. 2Fig. 3.7: Sistemas Hamiltonianos y gradiente en el espacio de parámetros ∆-τ.

12Fig. 3.8: Familias de trayectorias cerradas. Péndulo simple (a) . Sistema predador-presa (b) .Ejemplo 3.8 Sistema predador-presa (Volterra)Las ecuaciones del sistema predador-presa sonẋ 1 = −x 1 + x 1 x 2 ,ẋ 2 = x 2 − x 1 x 2 .Se intenta calcular las posibles trayectorias cerradas planteando una función V de la formaV (x 1,x 2)=h 1(x 1)+h 2(x 2),donde h 1 (·) y h 2 (·) se elegirán de modo de anular ˙V sobre las trayectorias del sistema (3.15). Entonces,˙V (x 1 ,x 2 ) = h 0 1(x 1 )ẋ 1 + h 0 2(x 2 )ẋ 2Para que ˙V sea idénticamente cero es necesario que= h 0 1(x 1)(−x 1 + x 1x 2)+h 0 2(x 2)(x 2 − x 1x 2).h 0 1(x 1 )x 1 (x 2 − 1) = h 0 2(x 2 )x 2 (1 − x 1 )=0,(3.15)que puede escribirse comoh 0 x 11(x 1)(1 − x 1 ) = x 2h0 2(x 2)(1 − x 2 ) .El miembro izquierdo de la ecuación es sólo función de x 1 e independiente de x 2 , mientras que el de laderecha es función sólo de x 2 e independiente de x 1 . En consecuencia ambos deben ser iguales a unaconstante k; en otras palabrasLa solución de (3.16) esx 1x 2h 0 1(x 1 )(1 − x = k, 1) h0 2(x 2 ) = k. (3.16)(1 − x 2)h 1 (x 1 )=k(ln x 1 − x 1 ), h 2 (x 2 )=k(ln x 2 − x 2 ).Por lo tanto una función V apropiada para este ejemplo esV (x 1,x 2)=lnx 1 − x 1 +lnx 2 − x 2,donde, sin pérdida de generalidad, se ha supuesto que k =1. Para esta elección de V cualquier conjuntoS c de la forma (3.13) (con c>0) es una curva cerrada, de manera que la familia de curvas definidas porln x 1 − x 1 +lnx 2 − x 2 = constanteconstituyen un conjunto de trayectorias cerradas para el sistema predador-presa como muestra la Fig. 3.8(b).En este ejemplo V está definida solamente en el primer cuadrante (x 1 > 0, x 2 > 0). 2

3.3. MÉTODO ANALÍTICO PARA CALCULAR SOLUCIONES PERIÓDICAS 13La función auxiliar V (x 1 ,x 2 ) del Ejemplo 3.7 (péndulo sin amortiguamiento) coincide con la funciónHamiltoniana del sistema; sin embargo la función V (x 1 ,x 2 ) delEjemplo3.8(sistemapredadorpresa)no califica como tal ya queẋ 1 = x 1 − x 1 x 2 6= ∂V (x 1,x 2 )∂x 2= 1 x 2− 1,ẋ 2 = −x 2 + x 1 x 2 6= − ∂V (x 1,x 2 )= − 1 +1.∂x 1 x 1Sin embargo, se puede encontrar una transformación de coordenadas tal que en las nuevas variablesel sistema de Lotka-Volterra (3.15) sea Hamiltoniano. Definiendo las variables x, y comox 1 = e x , x 2 = e y ,que son válidas sólo para x 1 > 0, x 2 > 0, se tiene queẋ 1 = e x ẋ = e x − e x e y ,ẋ 2 = e y ẏ = −e y + e x e y ,de donde resultaẋ =1− e y ,ẏ = −1+e x .Este sistema es Hamiltoniano con función de energía total(3.17)H(x, y) =x − e x + y − e y ,yseverifica trivialmente que ẋ = ∂H/∂y, ẏ = −∂H/∂x. Una primera integral del sistema (3.17)es H(x, y) =constante; y en consecuencia una primera integral del sistema (3.15) esque coincide con la calculada en el Ejemplo 3.8.ln x 1 − x 1 +lnx 2 − x 2 = constante,ReferenciasE. Atlee Jackson, Perspectives of Nonlinear Dynamics, Vol. 1, Cambridge University Press, Cambidge,1989.L. Perko, Differential Equations and Dynamical Systems, 2da. Ed., Texts in Applied Mathematics7, Springer-Verlag, New York, 1996.B. Nuriyev, T.Ergenç, Exact Solutions of Two-Dimensional Lokta-Volterra Equations, (online):http://citeseer.ist.psu.edu/105038.html.M. Vidyasagar, Nonlinear Systems Analysis, 2da. Ed., Prentice-Hall Inc., 1993, pp. 75-78.S. Wiggins, Introduction to Applied Nonlinear Dynamical Systems, Text in Applied Mathematics,Springer-Verlag, New York, 1990.