Statistik Multi-dimensi

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005Statistik Multi-dimensiContoh: Dalam kasus dua variabel acak ˜x dan ỹ yangmemiliki dua fungsi distribusi kumulatif dua-dimensi F (x, y).Maka probabilitas bersama untuk munculnya nilai ˜x < x dannilai ỹ < y diberikan dalam formulasiF (x, y) = P (˜x < x, ỹ < y)Fungsi padat probabilitas dua-dimensif(x, y) = ∂2 F (x,y)∂x∂y– Typeset by FoilTEX – 1

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005Karena 0 ≤ P ≤ 1 makalimx → −∞y → −∞F (x, y) = 0 danlimx → +∞y → +∞F (x, y) = +1.Probabilitas bahwa kedua variabel acak muncul antara ˜x 1dan ˜x 2 serta ˜x 1 dan ˜x 2 adalahP (x 1 < ˜x < x 2 ; y 1 < ỹ < y 2 ) = ∫ x 2x 1∫ y2y 1f(u, v)dudv– Typeset by FoilTEX – 2

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005Untuk variabel acak n-dimensif(x) = f(x 1 , x 2 , · · · , x n )F (x) = F (x i , x 2 , · · · , x n )untuk nilai ˜x < x= P (˜x < x) = P (˜x 1 < x 1 , ˜x 2 < x 2 , · · · , ˜x n < x n , )= ∫ x 1∫ x2−∞ −∞ · · · ∫ x n−∞ f(u 1, u 2 , · · · , u n )du 1 du 2 · · · du n– Typeset by FoilTEX – 3

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005kovariansih(˜x, ỹ) = [(˜x − E(˜x))(ỹ − E(ỹ))] = [(˜x − µ x )(ỹ − µ y )]makacov(˜x, ỹ) = σ xy = E[h(˜x, ỹ)] = E[(˜x − µ x )(ỹ − µ y )]atauσ xy = ∫ ∞−∞∫ ∞−∞ (x − µ x)(y − µ y )f(x, y)dxdyKoefisien korelasiρ xy = σ xyσ x σ y= E{ (˜x−E(˜x)σ x· (ỹ−E(ỹ))σ y}– Typeset by FoilTEX – 4

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005untuk kasus dua-dimensi semacam ini ada tiga momen pusatderajat dua. ¯m 10 dan ¯m 01 adalah momen-momen pertama(nilai ekspektasi) untuk variabel ˜x dan ỹ. Dan tiga momenpusat derajat duanya adalah:m 20 = E{(˜x − ¯m 10 ) 2 } = E((˜x − µ x ) 2 ) = σx2m 02 = E{(ỹ − ¯m 01 ) 2 } = E((ỹ − µ y ) 2 ) = σy2m 11 = E{(˜x − ¯m 10 )(ỹ − ¯m 01 )} = E((˜x − µ x )(ỹ − µ y )) = σ xy– Typeset by FoilTEX – 6

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005untuk kasus vektor variabel acak n-dimensi ˜xM =⎡⎢⎣⎤m x1 x 1m x1 x 2· · · m x1 x nm x2 x 1m x2 x 2· · · m x2 x n⎥.⎦m xn x 1m xn x 2· · · m xn x n=⎡⎢⎣⎤σx 2 1σ x1 x 2· · · σ x1 x nσ x2 x 1σx 2 2· · · σ x2 x n⎥.⎦σ xn x 1σ xn x 2· · · σx 2 n– Typeset by FoilTEX – 7

GD2212 - Hitung Perataan I B. Setyadji, Maret 2005Distribusi MultinormalFungsi padat untuk distribusi multinormal vektor random[ ]1f(x 1 , x 2 , · · · , x n ) =(2π) n/2√ |Σ|×exp [ − 1 2 (x − µ x) t Σ −1 (x − µ x ) ]1f(x, y) = √ exp{− σ2 1 σ2 2(2π) σ1 2σ2 2 −σ2 2(σ 2 121 σ2 2 −σ2 12 )[(x−µ)2σ 2 1− 2σ 12(x−µ 1 )(y−µ 2 )σ 2 1 σ2 2]+ (y−µ 2) 2}σ22– Typeset by FoilTEX – 8

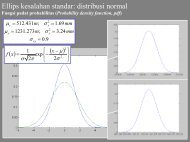
GD2212 - Hitung Perataan I B. Setyadji, Maret 2005f(y|x) = 1¯σ √ 2π= {1 −(y−µ(x))22¯σ 2 }dengan nilai menengah sebagai fungsi dari xµ(x) = µ 2 + ρσ 2σ 1(x − µ 1 ) = µ 2 + σ 12σ 1(x − m u 1 )dan variansi¯σ 2 = σ 2 2(1 − ρ 2 ) = σ2 1 σ2 2 −σ2 12σ 2 1– Typeset by FoilTEX – 9