ÃημαÄα και ÃÃ…ÃÄημαÄα-i
ÃημαÄα και ÃÃ…ÃÄημαÄα-i
ÃημαÄα και ÃÃ…ÃÄημαÄα-i
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
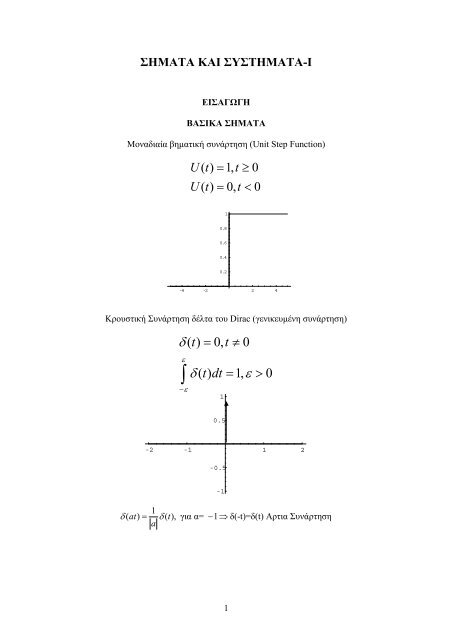
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I<br />
ΕΙΣΑΓΩΓΗ<br />
ΒΑΣΙΚΑ ΣΗΜΑΤΑ<br />
Μοναδιαία βηµατική συνάρτηση (Unit Step Function)<br />
Ut () = 1, t≥<br />
0<br />
Ut () = 0, t<<br />
0<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
-4 -2 2 4<br />
Κρουστική Συνάρτηση δέλτα του Dirac (γενικευµένη συνάρτηση)<br />
δ () t = 0, t ≠ 0<br />
ε<br />
∫<br />
−ε<br />
δ() tdt= 1, ε > 0<br />
1<br />
0.5<br />
-2 -1 1 2<br />
-0.5<br />
-1<br />
1<br />
δ( at) = δ( t), για α= −1⇒<br />
δ(-t)=δ(t) Αρτια Συνάρτηση<br />
a<br />
1
du()<br />
t<br />
δ () t =<br />
dt<br />
ΧΡΟΝΙΚΕΣ ΜΕΤΑΤΟΠΙΣΕΙΣ<br />
u(t+2)<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
-5 -4 -3 -2 -1 1<br />
u(t-2)<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
-4 -2 2 4<br />
δ ( t + 2)<br />
1<br />
0.5<br />
-4 -2 2 4<br />
-0.5<br />
-1<br />
2
δ ( t + 2)<br />
1<br />
0.5<br />
-4 -2 2 4<br />
-0.5<br />
-1<br />
Μοναδιαία Συνάρτηση Ράµπας<br />
τ<br />
ut ( + )<br />
2<br />
Τετραγωνικός Παλµός<br />
τ τ<br />
Pτ<br />
() t = 1, − ≤ t <<br />
2 2<br />
P() t = 0, αλλού<br />
τ<br />
3
1<br />
0.5<br />
-4 -2 2 4<br />
-0.5<br />
-1<br />
1<br />
ut ( + τ /2)<br />
-τ/2<br />
τ/2<br />
−ut<br />
( −τ<br />
/2)<br />
1<br />
ut ( τ τ<br />
+ ) −ut ( − ) = p τ<br />
2 2<br />
4
ΓΝΩΣΤΑ ΗΜΙΤΟΝΟΕΙ∆Η ΚΑΙ ΕΚΘΕΤΙΚΑ ΣΗΜΑΤΑ<br />
yt () = e − at<br />
yt () = sinωt<br />
1<br />
0.5<br />
-7.5 -5 -2.5 2.5 5 7.5<br />
-0.5<br />
-1<br />
ΤΥΠΟΣ ΤΟΥ EULER<br />
jωt<br />
e = Cosωt + j sinωt<br />
5
ΜΕΣΗ ΤΙΜΗ ΣΗΜΑΤΟΣ<br />
2<br />
1<br />
Xt () = xtdt () (1)<br />
t − t<br />
∫<br />
t<br />
2 1 t<br />
1<br />
ΠΕΡΙΟ∆ΙΚΟ ΣΗΜΑ ΜΕ ΠΕΡΙΟ∆Ο Τ<br />
T<br />
1<br />
X(t)= xtdt ( ) (2)<br />
T<br />
∫<br />
0<br />
ΕΝΕΡΓΟΣ ΤΙΜΗ(RMS)<br />
t<br />
2<br />
1<br />
1 2 2<br />
X(t)=[ x ( t) dt] (3)<br />
t − t<br />
∫<br />
2 1 t<br />
1<br />
Παράδειγµα<br />
A<br />
Ενεργ ός Τ ιµ ή του x(t)=Asinωt απο την (3) έχουµε x(t)=<br />
2<br />
Κάθε σήµα (συνάρτηση του χρόνου) µπορεί να γραφτεί σαν το άθροισµα ενός άρτιου<br />
και ενός περιτού σήµατος.<br />
x() t = xeven<br />
() t + xodd<br />
() t<br />
1<br />
xeven() t = [ x() t + x( −t)]<br />
2<br />
1<br />
xodd<br />
() t = [ x() t −x( −t)]<br />
2<br />
Ι∆ΙΟΤΗΤΑ ∆ΕΙΓΜΑΤΟΛΗΨΙΑΣ ΤΗΣ δ(t):<br />
∫<br />
f() t δ ( t− t ) = f( t )<br />
0 0<br />
Για<br />
t=0 έχουµε f(t)δ(t)=f(0)<br />
∫<br />
ΠΕΡΙΟ∆ΙΚΟ ΣΗΜΑ: Υπάρχει σταθερά Τ (περίοδος) για την οποία ισχύει:<br />
xt ( + Τ ) = xt ( ), −∞< t
ΣΗΜΑ ΕΝΕΡΓΕΙΑΣ (ΟΛΑ ΤΑ ΦΥΣΙΚΑ ΣΗΜΑΤΑ):<br />
∫<br />
E = x 2 () t dt <br />
ΣΥΣΤΗΜΑΤΑ ΣΥΝΕΧΟΥΣ ΧΡΟΝΟΥ ΜΙΑΣ ΕΙΣΟ∆ΟΥ ΚΑΙ ΜΙΑΣ ΕΞΟ∆ΟΥ<br />
Αδιαφανές<br />
Μαύρο κουτί<br />
(Black Box)<br />
X(t)<br />
F<br />
Y(t)<br />
ΣΧΕΣΗ ΕΙΣΟ∆ΟΥ-ΕΞΟ∆ΟΥ<br />
{ }<br />
Yt () = F xt ()<br />
Γενικώς,η τιµή της εξόδου την χρονική στιγµή t εξαρτάται απο όλες τις τιµές της<br />
εισόδου x(t) µέχρι και την χρονική στιγµή t και όχι µόνο απο την τιµή της εισόδου<br />
x(t) την χρονική στιγµή t.<br />
AITIOTHTA<br />
Ενα σύστηµα Yt () F{ xt ()}<br />
t<br />
0<br />
, η έξοδος<br />
0<br />
= λέγεται αιτιατό (φυσικό) εαν, για κάθε χρονική στιγµή<br />
yt ( ) του συστήµατος εξαρτάται µόνο απο την είσοδο x(t) µέχρι την<br />
χρονική στιγµή t 0<br />
.<br />
7
∆ηλαδή η έξοδος δεν εξαρτάται απο µελλοντικές τιµές της εισόδου. Όλα τα φυσικά<br />
συστήµατα είναι αιτιατά. Μη-αιτιατά δεν υπάρχουν στον φυσικό κόσµο, µπορούν<br />
όµως να προσεγγιστούν µε χρονο-καθυστερήσεις.<br />
Παράδειγµα<br />
Το σύστηµα yt () = xt ( − 1) είναι αιτιατό<br />
Το σύστηµα yt () = xt ( + 1) είναι µη αιτιατό.<br />
ΣΥΣΤΗΜΑΤΑ ΧΡΟΝΙΚΑ ΑΝΑΛΛΟΙΩΤΑ (ΑΜΕΤΑΒΛΗΤΑ)<br />
Ενα σύστηµα yt () = F{ xt ()} αν για κάθε t 1<br />
,η έξοδος στην είσοδο x( t− t1)<br />
είναι η<br />
yt ( − t1)<br />
. ∆ηλαδή F{( x t− t1)}<br />
= yt ( − t1)<br />
.<br />
Χρονική ολίσθηση στο σήµα εισόδου, οδηγεί σε αντίστοιχη ολίσθηση στο σήµα<br />
εξόδου.<br />
8
Αδιαφανές<br />
Μαύρο κουτί<br />
(Black Box)<br />
X(t)<br />
F<br />
Y(t)<br />
x()<br />
t<br />
Yt ()<br />
x( t−<br />
t )<br />
1<br />
Yt ( − t)<br />
1<br />
9
Ένα αιτιατό σύστηµα yt () = F{ xt ()} δεν έχει µνήµη αν για κάθε t 1<br />
η έξοδος yt (<br />
1)<br />
εξαρτάται µόνο απο την τιµή της εισόδου x( t<br />
1)<br />
την χρονική στιγµή t 1<br />
. Το σύστηµα<br />
αυτό ονοµάζεται και στιγµιαίο.<br />
Π.χ. το σύστηµα yt () = kxt () δεν έχει µνήµη. Είναι ενισχυτής για κ>1 και<br />
εξασθενητής για κ
ΚΡΟΥΣΤΙΚΗ ΑΠΟΚΡΙΣΗ ΣΥΣΤΗΜΑΤΟΣ(IMPULSE RESPONSE)<br />
Αδιαφανές<br />
Μαύρο κουτί<br />
(Black Box)<br />
X(t)<br />
F<br />
Y(t)<br />
Έστω το σύστηµα F το οποίο είναι γραµµικό και χρονοαµετάβλητο. Κρουστική<br />
απόκριση ονοµάζεται η έξοδος του συστήµατος για είσοδο x() t = δ () t , την<br />
συνάρτηση Dirac.<br />
Αδιαφανές<br />
Μαύρο κουτί<br />
(Black Box)<br />
δ(t)<br />
F<br />
h(t)<br />
Κρουστική<br />
απόκριση<br />
ht () = F{ δ ()} t<br />
Αν γράψουµε την x() t = ∫ x( τ ) δ( t−τ)<br />
dτ<br />
σύµφωνα µε την ιδιοτητα δειγµατοληψίας<br />
της συνάρτησης δ τότε<br />
∫ ∫ ∫ δηλαδή<br />
yt () = F{ xt ()} = F{ x( τ ) δ( t− τ) dτ} = x( τ) F{ δ( t− τ} dτ = x( τ) ht ( −τ)<br />
dτ<br />
11
∫<br />
yt () = x( τ ) ht ( −τ)<br />
dτ<br />
ΣΥΝΕΛΙΚΤΙΚΟ ΟΛΟΚΛΗΡΩΜΑ<br />
(CONVOLUTION INTEGRAL)<br />
∫<br />
yt () = x( τ ) ht ( −τ)<br />
dτ<br />
Εποµένως, εαν γνωρίζουµε την κρουστική απόκτριση ενός γραµµικούχρονοαµετάβλητου<br />
συστήµατος,µπορούµε να υπολογίσουµε την έξοδο του για<br />
οποιαδήποτε είσοδο χ(t) µεσω του συνελικτικού ολοκληρώµατος.<br />
ΣΥΝΕΛΙΞΗ (CONVOLUTION)<br />
yt () = xt ()* ht () = x( τ ) ht ( −τ)<br />
dτ<br />
∫<br />
Παράδειγµα<br />
−at<br />
Να υπολογιστεί η συνέλιξη yt () = xt ()* ht () οταν xt () = e ut (), a> 0και<br />
ht () = ut ().u(t) είναι η µοναδιαία βηµατική συνάρτηση(unit step function)<br />
ut ( − τ ), t<<br />
0<br />
t<br />
1<br />
τ<br />
ut ( − τ ), t><br />
0<br />
1<br />
t<br />
τ<br />
1<br />
t<br />
τ<br />
Το γινόµενο µέσα στο ολοκλήρωµα είναι ≠ 0 µόνο για 0 < τ < tt , > 0<br />
Για t < 0 εχουµε x( τ ) h( t− τ ) = 0<br />
12
Για t > 0 έχουµε<br />
−ατ<br />
x( τ) ht ( − τ) = e ,0< τ < t<br />
x( τ ) h( t− τ) = 0, αλλου<br />
t<br />
−aτ<br />
1 −aτ<br />
t 1 −at<br />
Αρα για t>0 εχουµε yt () = ∫ e dτ<br />
= [ − e ]<br />
0<br />
= (1 −e ) ut ()<br />
α a<br />
0<br />
1/a<br />
t<br />
Λύση:<br />
1 −at<br />
yt () = (1 − e ) ut ()<br />
a<br />
Ι∆ΙΟΤΗΤΕΣ ΤΗΣ ΣΥΝΕΛΙΞΗΣ<br />
∫<br />
yt () = x( τ ) ht ( −τ)<br />
dτ<br />
Γενικά ισχύει f1()* t f2() t = f1( τ ) f2( t−τ)<br />
dτ<br />
• Αντιµεταθετική f1()* t f2() t = f2()* t f1()<br />
t<br />
• Προσεταιριστική [ f1()* t f2()]* t f3() t = f1()*[ t f2()* t f3()]<br />
t<br />
∫<br />
• Συνέλιξη µε δ(t) δίνει την<br />
f(t): f ( t)* δ( t) = δ( t)* f( t) = δ( τ) f( t− τ) dτ<br />
= f( t)<br />
∫<br />
13
• Ιδιότητα δειγµατοληψίας της δ του Dirac: f () tdt ( − t0) dt=<br />
f( t0)<br />
• Επιµεριστική ιδιότητα: f1()*[ t f2() t + f3()] t = f1()* t f2() t + f1()* t f3()<br />
t<br />
∫<br />
ΣΕΙΡΕΣ FOURIER<br />
a<br />
f t a n t b n t<br />
∞<br />
0<br />
() = + ∑[ ncos ω0 +<br />
nsin ω0<br />
]<br />
2 n=<br />
1<br />
2 π<br />
ω0 = sπ<br />
f0<br />
= , T η περιοδος του σηµατος<br />
T<br />
ΜΟΝΟ ΓΙΑ ΠΕΡΙΟ∆ΙΚΑ ΣΗΜΑΤΑ!!!<br />
Οι συντελεστες a , b υπολογίζονται σε µία περίοδο:<br />
n<br />
a<br />
0<br />
n<br />
t1<br />
+ T<br />
2<br />
=<br />
T<br />
∫<br />
t1<br />
t1<br />
+ T<br />
t1<br />
t1<br />
+ T<br />
f()<br />
t dt<br />
2<br />
an<br />
= f()cos<br />
t ω<br />
n 0<br />
0tdt<br />
><br />
T<br />
∫<br />
2<br />
bn<br />
= f()sin<br />
t ω0tdt<br />
T<br />
∫<br />
t1<br />
Βιβλίο Fourier:”Théorie analytique de la chaleur” 1822. Μετάδοση Θερµότητας<br />
Μαθηµατικες συνθήκες για σύγκλιση (Ικανές αλλα όχι απαραίτητες) Dirichlet<br />
(1829):<br />
1.<br />
t1<br />
+ T<br />
∫<br />
t1<br />
f()<br />
t dt < ∞ ,πεπερασµένο<br />
2. Πεπερασµένο πλήθος min-max και ασυνεχειών σε µια περίοδο<br />
Στις ασυνέχειες το ανάπτυγµα Fourier συγκλίνει στο 1 − +<br />
f ( t0) = [ f( t0) + f( t0)]<br />
2<br />
ΑΝΑΠΤΥΓΜΑ FOURIER ΜΟΝΟ ΜΕ COS KAI ΑΣΚΗΣΕΙΣ:<br />
∞<br />
∑<br />
f() t = A + A cos( nω<br />
t+<br />
θ )<br />
0 n<br />
0<br />
n=<br />
1<br />
a<br />
A A a b<br />
0<br />
2 2 −1<br />
n<br />
0<br />
= ,<br />
n<br />
=<br />
n<br />
+<br />
n<br />
, θn<br />
=− tan ( )<br />
2<br />
an<br />
n<br />
b<br />
14
ΕΚΘΕΤΙΚΗ-ΜΙΓΑ∆ΙΚΗ ΜΟΡΦΗ ΣΕΙΡΑΣ FOURIER<br />
∞<br />
f () t = ∑ cne ω<br />
n=−∞<br />
in 0t<br />
t1<br />
+ T<br />
1<br />
−inω0t<br />
cn<br />
= f()<br />
t e dt<br />
T<br />
∫<br />
t1<br />
Οι συναρτήσεις<br />
inω0t<br />
e<br />
Φ<br />
n()<br />
t = αποτελούν πλήρη βάση συναρτήσεων<br />
T<br />
∆ΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ:<br />
ΣΧΕΣΕΙΣ:<br />
Parseval: Ενέργεια σήµατος = Ε =<br />
t1<br />
∫<br />
t1<br />
Ta T T<br />
f tdt a b TA A T c<br />
2 ∞ ∞ ∞<br />
2 0<br />
2 2 2 2 2<br />
() = + ∑( n<br />
+<br />
n)<br />
= + ∑ n<br />
= ∑ n<br />
4 2 n= 1 2 n= 1<br />
n=−∞<br />
ΠΑΡΑ∆ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER<br />
Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):<br />
∞<br />
∑<br />
St () = δτ ( −kT)<br />
k =−∞<br />
1 1 1<br />
c s t e dt e<br />
T T T<br />
T<br />
2 −inω0t −inω0 ()<br />
0<br />
n<br />
= ∫ T<br />
= =<br />
−<br />
2<br />
∫<br />
∞<br />
∆ιότι f () t δ ( t− t0) dt = f( t0)<br />
−∞<br />
∞<br />
1<br />
st () = ∑ e<br />
T<br />
n=−∞<br />
inω0t<br />
15
S(t)<br />
t<br />
-2T -T<br />
T<br />
2T<br />
ΠΑΡΑ∆ΕΙΓΜΑ 2 ΣΕΙΡΑΣ FOURIER<br />
Ανάπτυξη σειράς παλµών σε σειρά Fourier (εκθετική)<br />
τ<br />
Pτ<br />
() t = 1, t ≤<br />
2<br />
τ<br />
Pτ<br />
() t = 0, t ><br />
2<br />
−Τ<br />
τ<br />
−<br />
2<br />
τ<br />
2<br />
Τ<br />
st () = p( t−kT)<br />
k =−∞<br />
T<br />
τ τ τ<br />
jn<br />
2 2 0 jn<br />
in<br />
0<br />
0t<br />
τ<br />
− ω ω<br />
− ω<br />
2 2<br />
−inω0t −inω0t<br />
e e − e<br />
nω 2<br />
0τ<br />
∫ () ∫<br />
[ ]<br />
τ<br />
[ ] sin( )<br />
T<br />
τ<br />
− ω −<br />
0 2<br />
− ω0 ω0<br />
2<br />
−<br />
−<br />
2 2<br />
1 1 1 1 2<br />
cn<br />
= s t e dt = e dt = = =<br />
T T T jn T jn Tn<br />
c<br />
n<br />
∞<br />
∑<br />
τ<br />
τ<br />
sin( nω<br />
)<br />
τ<br />
τ<br />
= =<br />
T τ<br />
nω<br />
T<br />
0<br />
2<br />
nωτ<br />
2<br />
0<br />
2 0<br />
sin c( )<br />
Αφού ισχύουν:<br />
sin x<br />
sin cx ( ) =<br />
x<br />
n ωτ 0<br />
n2<br />
= π τ = nπ( τ )<br />
2 2T<br />
T<br />
16
c<br />
Εποµένως:<br />
n<br />
τ τ<br />
= ( )sin c( nπ<br />
( ))<br />
T Τ<br />
Και το ανάπτυγµα Fourier της παλµοσειράς είναι:<br />
τ nπτ<br />
st = ∑ c e<br />
T T<br />
∞<br />
0<br />
() sin [ ] in ω t<br />
n=−∞<br />
ΣΕΙΡΑ FOURIER ΣΥΝΗΜΙΤΟΝΩΝ<br />
∞<br />
τ τ nπτ<br />
s() t = + 2 ∑ sin c( )cosnω<br />
0t<br />
T T T<br />
n=<br />
1<br />
DC ορος(σταθερός)<br />
n-στή αρµονική<br />
Ισχύς του σήµατος της παλµοσειράς s(t):<br />
τ<br />
τ<br />
2<br />
E 1<br />
2 2 1<br />
P ∫ τ s () t dt dt<br />
−<br />
∫<br />
2<br />
τ<br />
−<br />
2<br />
τ<br />
= = = =<br />
T T T T<br />
17
τ<br />
Ισχυς του DC όρου: P0 = c0 = ( )<br />
T<br />
2 2<br />
2 2 2 τ 2 2 nπτ<br />
a<br />
Ισχύς της n-στής αρµονικής: Pn = cn + c−n = 2 cn<br />
= 2( ) sin c ( ) =<br />
T T 2<br />
(RMS τιµή ηµιτονοειδούς σήµατος =<br />
2<br />
a<br />
n )<br />
2<br />
ΠΟΣΟΣΤΟ ΙΣΧΥΟΣ ΤΗΣ Ν-ΟΣΤΗΣ ΑΡΜΟΝΙΚΗΣ:<br />
p<br />
n<br />
p<br />
τ nπτ<br />
= = i c<br />
P T T<br />
n<br />
2<br />
100 % 100 2( )sin ( )<br />
Π.χ. γιά duty cycle = 20%=|t/T=1/5 έχουµε<br />
τ<br />
p = 100( ) = 20%<br />
0<br />
Τ<br />
1 nπ<br />
nπ<br />
pn<br />
= i c = c<br />
5 2 2<br />
2 π<br />
p1<br />
= 40sin c ( ) = 35%<br />
5<br />
2 2π<br />
p2<br />
= 40sin c ( ) = 23%<br />
5<br />
2 3π<br />
p3<br />
= 40sin c ( ) = 10%<br />
5<br />
2 2<br />
100 2( )sin ( ) 40sin ( )<br />
Για<br />
η<br />
n= 5k → p5k<br />
= 0, k = 1, 2,3,..... H 5 ,10 η , κτλ αρµονικές είναι µηδενικές<br />
p + p + p + p = 88% της ισχύος στους 4 πρώτους όρους=DC όρος + 3 αρµονικές<br />
0 1 2 3<br />
τ 1<br />
Για Duty cycle=50%, = έχουµε:<br />
T 2<br />
18
1<br />
p0<br />
= 100 = 50%<br />
2<br />
2 nπ<br />
pn<br />
= 100sin c ( )<br />
2<br />
2 π<br />
p1<br />
= 100sin c ( ) = 40,5%<br />
2<br />
2 2π<br />
p2<br />
= 100sin c ( ) = 0<br />
2<br />
2 3π<br />
p3<br />
= 100sin c ( ) = 4,5%<br />
2<br />
p + p + p + p = 95% της ισχύος στους 4 πρώτους όρους<br />
0 1 2 3<br />
Οι p<br />
2k<br />
= 0 , άρτιες αρµονικές είναι µηδενικές.<br />
ΕΠΟΜΕΝΩΣ: Πλουσιότερο φάσµα για µικρό duty cycle.<br />
2<br />
sin c<br />
∞<br />
∑<br />
st () = A+ Acos( nω<br />
t+<br />
θ )<br />
0 n<br />
0<br />
n=<br />
1<br />
τ 1<br />
A0<br />
= = = 0.2<br />
T 5<br />
n<br />
19
A n<br />
0.37<br />
0.3 0.21<br />
τ nπτ<br />
An<br />
= 2 sin c( ), n=<br />
1,2,3,...<br />
T T<br />
1 π<br />
A1<br />
= 2 sin c( ) = 0.37<br />
5 5<br />
1 2π<br />
A2<br />
= 2 sin c( ) = 0.3<br />
5 5<br />
1 3π<br />
A3<br />
= 2 sin c( ) = 0.21<br />
5 5<br />
1 4π<br />
A1<br />
= 2 sin c( ) = 0.09<br />
5 5<br />
A = 0<br />
5<br />
ΠΑΡΑ∆ΕΙΓΜΑ 3<br />
ΑΠΛΗ ΑΝΟΡΘΩΣΗ-ΑΝΑΠΤΥΞΗ ΗΜΙΑΝΟΡΘΩΜΕΝΗΣ ΤΑΣΗΣ ΣΕ ΣΕΙΡΑ<br />
FOURIER(AC->DC)<br />
20
D1: Ιδανική δίοδος<br />
V () t = Acos( ω t), u () t > 0<br />
L<br />
2<br />
0 2<br />
V () t = 0, u () t ≤ 0<br />
L<br />
T<br />
2<br />
1<br />
−inω0t<br />
cn<br />
= Acosω0te dt<br />
T<br />
∫<br />
T<br />
−<br />
2<br />
e<br />
cos( ω t)<br />
=<br />
0<br />
+ e<br />
2<br />
iω0t −iω0t<br />
T T T<br />
2 4 4<br />
−i( n−1) ω0t T<br />
− i( n+<br />
1) ω0t<br />
T<br />
A iω0t −inω0t −iω0t inω0t A −i( n−1) ω 1<br />
0t − i( n+<br />
1) ω0t<br />
A e A e<br />
4 4<br />
n<br />
[ ] [ ]<br />
T<br />
[ ]<br />
T<br />
2T ∫<br />
T 2T ∫<br />
T 2T ∫<br />
T<br />
2 T −j( n−1) ω −<br />
0 4<br />
2 T − j( n+<br />
1) ω −<br />
0 4<br />
− − −<br />
2 4 4<br />
c = e e + e e dt = e dt + e dt = + =<br />
T T T T<br />
T T<br />
−i( n−1) ω0 i( n−1) ω0 − i( n+ 1) ω0 i( n+ 1) ω0<br />
4 4 4 4 sin[( n− 1) ω0 ] sin[( n+<br />
1) ω0<br />
]<br />
A e −e A e −e A<br />
= [ ] [ ]<br />
4 A<br />
+ = +<br />
4<br />
2 T −j( n−1) ω 2 T − j( n+ 1) ω T ( n− 1) ω T ( n+<br />
1) ω<br />
2π<br />
ω0T<br />
= T = 2π<br />
T<br />
0 0 0 0<br />
εποµένως:<br />
c<br />
n<br />
π π<br />
sin( n− 1) sin( n+<br />
1)<br />
A<br />
= [ 2 + 2]<br />
2π<br />
n− 1 n+<br />
1<br />
21
ΑΣΚΗΣΗ. ΝΑ ΥΠΟΛΟΓΙΣΤΕΙ Η ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΣΕΙΡΑ FOURIER ΤΟΥ<br />
ΤΕΤΡΑΓΩΝΙΚΟΥ ΣΗΜΑΤΟΣ<br />
Σε µία περίοδο<br />
T<br />
f () t = −A, − < t < 0<br />
2<br />
T<br />
f() t = A,0< t <<br />
2<br />
Έχουµε:<br />
T<br />
T<br />
2 0<br />
2<br />
1 1<br />
a0<br />
= f() t dt = [ − Adt+ Adt] = 0<br />
T T<br />
∫ ∫ ∫ εποµένως το τετραγωνικό σήµα δεν έχει<br />
T<br />
T<br />
−<br />
−<br />
2 2<br />
0<br />
συνεχή (DC) συνιστώσα (Μέσος όρος µηδέν).<br />
T<br />
T<br />
2 0<br />
2<br />
2 2<br />
an<br />
= f ( t) cos nω tdt = [ − Acos nω tdt + Acos nω<br />
tdt] = 0∀n<br />
T<br />
∫ ∫ ∫<br />
0 0 0<br />
T<br />
T T<br />
−<br />
−<br />
0<br />
2 2<br />
Η σειρά δεν έχει συνηµιτονοειδείς όρους λόγω περιττής συµµετρίας( f ( − t) =− f( t)<br />
).<br />
T<br />
T<br />
2 0<br />
2<br />
T<br />
A cos nω0t 0 cos nω0t<br />
2<br />
∫ ω0 ∫ ω0 ∫ ω0 T<br />
0<br />
T<br />
T<br />
ω −<br />
0<br />
0 2<br />
ω0<br />
−<br />
−<br />
2 2<br />
2 2 2<br />
bn<br />
= f ( t)sin n tdt = [ − Asin n tdt + Asin n tdt] = {[ ] + [ − ] } =<br />
T T T n n<br />
0, n = αρτιο<br />
A<br />
2A<br />
= (cos 0 −cos( nπ) − cos( nπ) + cos 0) = [1 − cos( nπ)] = 4 A<br />
nπ nπ , n = περιττ ό<br />
nπ<br />
εποµένως:<br />
∞<br />
2A 1−<br />
cos( nπ<br />
) 4A<br />
1 1<br />
f( t) = ∑ sin nω0t = [sin nω0t+ sin 3ω0t+ sin 5 ω0t+<br />
....]<br />
π n=<br />
1 n<br />
π 3 5<br />
Για<br />
n=2k+1:<br />
∞<br />
4A<br />
1<br />
f() t = ∑ sin(2k+<br />
1) ω0t<br />
π 2k<br />
+ 1<br />
k = 0<br />
∞<br />
= A0<br />
∑ n<br />
ω0<br />
n=<br />
1<br />
2 2<br />
n<br />
=<br />
n<br />
+<br />
n<br />
=<br />
n<br />
f()<br />
t<br />
A a b b<br />
θ<br />
n=<br />
+ A cos( n t+<br />
θ )<br />
b<br />
− tan ( ) =−tan ( ∞ ) =−90<br />
a<br />
−1 n<br />
−1 0<br />
n<br />
n<br />
22
A n<br />
1,27A<br />
0.42A<br />
0.25A 0.18A<br />
n<br />
1 3 5 7<br />
1 3 5 7<br />
0<br />
−90<br />
ΑΣΚΗΣΗ<br />
Έστω οι ορθοκανονικές συναρτήσεις φ () t στο διάστηµα [a,b]:<br />
i<br />
b<br />
∫<br />
a<br />
0, i ≠<br />
φi() t φj()<br />
t dt =<br />
1, i =<br />
j<br />
j<br />
Έστω η προσέγγιση της συνάρτησης f(t) από:<br />
N<br />
f<br />
() t = ∑ aiφi()<br />
t<br />
i=<br />
0<br />
Να επιλεγούν οι συντελεστές a<br />
i<br />
του παραπάνω αναπτύγµατος ώστε να<br />
23
N<br />
2 2<br />
ελαχιστοποιείται το RMS σφάλµα: S = [ f( t) − f<br />
( t)] dt = [ f( t) −∑ aiφi( t)] dt(1)<br />
∫<br />
a<br />
∫<br />
a<br />
i=<br />
0<br />
Λύση<br />
∂S<br />
Θα πρέπει = 0, k = 0,1,2,..., N<br />
∂ak<br />
Χρησιµοποιούµε το k για να µην µπερδευτούµε µε την µεταβλητή i του αθροίσµατος.<br />
Παραγωγίζουµε την (1) και έχουµε:<br />
∂S<br />
∂a<br />
k<br />
b<br />
∫<br />
N<br />
= 2 [ f ( t) − aφ<br />
( t)] φ ( t) dt = 0, k = 0,1,2,3,..., N<br />
a<br />
∑<br />
i=<br />
0<br />
i i k<br />
Ή ισοδύναµα:<br />
b<br />
∫ ∑ ∫<br />
a<br />
N<br />
f () t φ () t dt = a φ () t φ () t dt = a<br />
b<br />
k i i k k<br />
i=<br />
0 a<br />
b<br />
Αφού a φ () t φ () t dt ≠ 0 µόνο για i=k<br />
∫<br />
a<br />
i<br />
k<br />
Το άθροισµα στα δεξιά έχει έναν µόνο µη µηδενικό όρο, τον a<br />
k<br />
.Έτσι προκύπτει οτι<br />
b<br />
οι συντελεστές ∫ f () t φk<br />
() t dt ελαχιστοποιούν το RMS σφάλµα της προσέγγισης.<br />
a<br />
• Γενικευµένη ανάλυση FOURIER σε βάση ορθογώνιων συναρτήσεων<br />
• Ειδική περίπτωση η τριγωνοµετρική σειρά FOURIER περιοδικών<br />
συναρτήσεων σε ηµίτονα και συνηµίτονα µε αρµονικό λόγο<br />
συχνοτήτων. ω , 1,2,3,4,....<br />
n<br />
= kω0 k = ακέραια πολλαπλάσια µιας θεµελιώδους<br />
2π<br />
συχνότητας ω0 = = 2π<br />
f0<br />
T<br />
24
ΑΣΚΗΣΕΙΣ ΓΙΑ BONUS:<br />
ΑΣΚΗΣΗ 1.Ορθογωνικότητα των συναρτήσεων 1, cos nω0t,<br />
sinω 0t<br />
στο διάστηµα [0,1]<br />
Να αποδειχθούν οι σχέσεις:<br />
T<br />
∫<br />
0<br />
T<br />
∫<br />
0<br />
T<br />
∫<br />
0<br />
T<br />
∫<br />
0<br />
T<br />
∫<br />
0<br />
sin<br />
cos<br />
ω<br />
m<br />
0tsin<br />
n<br />
0tdt T m n<br />
ω<br />
m<br />
0tcos<br />
n<br />
0tdt = T m n<br />
0 0<br />
0<br />
ω<br />
ω<br />
0, m≠<br />
n<br />
=<br />
, =<br />
2<br />
0, m≠<br />
n<br />
,<br />
2<br />
sin mω<br />
tcos nω<br />
tdt = 0, ∀m,<br />
n<br />
sin mω<br />
tdt = 0, ∀m<br />
0, n ≠ 0<br />
cos nω0tdt<br />
=<br />
Tn , = 0<br />
=<br />
Άρτια συνάρτηση: µόνο συνηµιτονοειδείς όρους και χρονικά αµετάβλητες.<br />
Περιττή συνάρτηση:µόνο ηµιτονοειδείς όρους.<br />
ΑΣΚΗΣΗ 2. Υπολογίστε τις τιµές των ολοκληρωµάτων:<br />
a<br />
∫<br />
−a<br />
a<br />
∫<br />
−a<br />
4<br />
2<br />
( 2)[ δ( ) 3 δ( 2)]<br />
∫<br />
−4<br />
4<br />
2<br />
t [ δ( t) δ( t 2) δ( t 5)] dt<br />
∫<br />
−4<br />
δ()cos<br />
t ωtdt<br />
δ()sin<br />
t ωtdt<br />
t + t + t−<br />
dt<br />
+ + + +<br />
ΑΣΚΗΣΗ 3. Αναπτύξτε σε τριγωνοµετρική σειρά FOURIER:<br />
T<br />
−A, − < t < 0<br />
1. Το τετραγωνικό σήµα: f()<br />
t =<br />
2<br />
T<br />
A,0< t <<br />
2<br />
t T<br />
A(1+ 2 ), − ≤ t < 0<br />
2. Το τριγωνικό σήµα: f()<br />
t =<br />
T 2<br />
t T<br />
A(1−<br />
2 ), 0 < t ≤<br />
T 2<br />
25
ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER<br />
∞<br />
∫<br />
−iωt<br />
F( ω) = f( t) e dt = FT[ f( t)]<br />
−∞<br />
Αντίστροφος µετασχηµατισµός Fourier:<br />
+∞<br />
1<br />
iωt<br />
−1<br />
f() t = F( ω) e dω = FT [ F( ω)]<br />
2π<br />
∫<br />
−∞<br />
Ιδιότητες:<br />
Αν f(t) πραγµατική συνάρτηση του χρόνου τότε:<br />
F( ω) =R ( ω) + jI ( ω) = f( t)cos ωtdt−<br />
j f( t)sinωtdt<br />
f() t = f () t + f () t<br />
αρτια<br />
∞<br />
∫<br />
R ( ω) = f ( t)cos ωtdt<br />
=R ( ω)<br />
αρτια<br />
−∞<br />
+∞<br />
∫<br />
I ( ω) =− f ( t)sin ωtdt<br />
=I ( ω)<br />
−∞<br />
περιττ ή<br />
περιττη<br />
Οι άρτιες συναρτήσεις έχουνε πραγµατικό FT και οι περιττές φανταστικό.<br />
∞<br />
∫<br />
−∞<br />
Το πραγµατικό µέρος του FT είναι άρτια συνάρτηση ενώ το φανταστικό µέρος είναι<br />
περιττή συνάρτηση του ω (αυτό ισχύει γενικά για µιγαδικό F.T.).<br />
αρτ<br />
περ<br />
∞<br />
∫<br />
−∞<br />
Παράδειγµα<br />
−at<br />
f() t = e u(), t a><br />
0<br />
∞ − ( a+<br />
jω<br />
) t<br />
−at − jωt − ( a+ jω) t − ( a+ jω)<br />
t e<br />
∞<br />
0<br />
( ω)<br />
0<br />
1<br />
F( ω) = ∫e u( t) e dt = ∫e dt = ∫e<br />
dt = [ ] =<br />
− a+ j a+<br />
jω<br />
1 a−<br />
jω<br />
a ω<br />
F( ω) = = = − j =R ( ω) + jI( ω)<br />
2 2 2 2 2 2<br />
a+ jω ω + a ω + a ω + a<br />
F( ω) = A( ω)<br />
e<br />
jφω<br />
( )<br />
1<br />
Α ( ω) = , Φ ( ω) =−tan<br />
2 2<br />
ω + a<br />
−1<br />
ω<br />
a<br />
26
e<br />
−at<br />
u()<br />
t<br />
ut ()<br />
Να υπολογιστεί ο µετασχηµατισµός FOURIER της συνάρτησης δ-Dirac:<br />
∫<br />
FT t t e dt e e<br />
− jωt − jωt − jω0<br />
{ δ( )} = δ( ) = t=<br />
0<br />
= = 1<br />
Αφού ισχύει οτι ∫ f () t δ () t dt = f(0)<br />
(ιδιότητα δειγµατοληψίας), εποµένως<br />
FT{ δ ( t)} = 1.<br />
δ () t<br />
FT<br />
1<br />
27
Να υπολογιστεί ο F.T. της συνάρτησης τετραγωνικού παλµού:<br />
Λύση<br />
T T<br />
1, − < t <<br />
Pτ<br />
() t = 2 2<br />
0, Αλλού<br />
1<br />
− T /2 T /2<br />
T T T<br />
T<br />
2 T<br />
jω<br />
− jω<br />
− jωt<br />
2 2<br />
sin( ω )<br />
−iωt<br />
− jωt<br />
e e − e 2 T<br />
2<br />
( ) ( ) [ ] sin( ) 2<br />
T<br />
Pτ<br />
ω = ∫Pτ<br />
t e dt = ∫ e dt =<br />
T<br />
= = ω = T = Tsin c( ω )<br />
T − jω −<br />
2<br />
jω ω 2 T<br />
ω<br />
2<br />
−<br />
2<br />
2<br />
sin x<br />
sin cx ( ) =<br />
x<br />
∆ίπλευρος εκθετικός παλµός<br />
−at<br />
e , t ≥ 0<br />
xt () =<br />
at<br />
e , t < 0<br />
0 ∞ ( a−jω) t −( a−jω)<br />
t<br />
at − jωt −at − jωt e 0 e<br />
∞<br />
∫ ∫<br />
−∞<br />
0<br />
−∞<br />
0<br />
1 1<br />
X( ω) = e e dt+ e e dt = [ ] + [ ] = + =<br />
( a− jω) ( a− jω) ( a− jω) ( a+<br />
jω)<br />
( a+ jω) + ( a−<br />
jω) 2a<br />
= =<br />
2 2 2 2<br />
a + ω a + ω<br />
28
Γραµµική ιδιότητα<br />
FT<br />
af () t + bf () t ↔ aF ( ω) + bF ( ω)<br />
1 2 1 2<br />
Συµµετρική ιδιότητα<br />
FT<br />
Αν f() t ↔ F( ω)<br />
FT<br />
Τότε Ft () ↔ 2 π f( − ω)<br />
Απόδειξη<br />
∞<br />
1<br />
jωt<br />
f () t = F( ω)<br />
e dω<br />
2π<br />
∫<br />
−∞<br />
∞<br />
∫<br />
jωt<br />
2 π f ( t) = F( ω)<br />
e dω<br />
−∞<br />
− jωt<br />
Εαν θέσουµε t =− t τότε 2 π f ( − t) = ∫ F( ω)<br />
e dω<br />
και όπου t<br />
∞<br />
−∞<br />
← ω και όπου ω ← t τότε έχουµε<br />
∞<br />
∫<br />
− jωt<br />
2 π f ( − ω) = Fte ( ) dt=<br />
FT{ f( t)}<br />
−∞<br />
Μετατόπιση στον χρόνο<br />
FT<br />
Αν f() t ↔ F( ω)<br />
j t0<br />
Τότε f( t−t ) ↔ F( ω)<br />
e − ω<br />
0<br />
Απόδειξη<br />
∞<br />
∫<br />
− jωt<br />
FT[ f ( t − t ] = f ( t −t ) e dt<br />
0) 0<br />
−∞<br />
Θέτουµε t− t0<br />
= ξ ,αλλαγή µεταβλητής οπότε t = t0<br />
+ ξ και dt = dξ<br />
∞<br />
∞<br />
− jωξ<br />
− jωt0 − jωt0 − jωξ<br />
− jωt0<br />
[ ( −<br />
0)] = ∫ ( ξ ) ξ = ∫ ( ξ) ξ = ( ω)<br />
−∞<br />
−∞<br />
FT f t t f e e d e f e d e F<br />
29
F( ω) = A( ω)<br />
e<br />
jφω<br />
( )<br />
j φω−ωt0<br />
Επειδή f( t−t ) ↔ A( ω)<br />
e<br />
0<br />
FT<br />
( ( ) )<br />
Μετατόπιση στον χρόνο ↔ Αλλαγή φάσης µόνο,το πλάτος παραµένει ως έχει<br />
Μετατόπιση στη συχνότητα-∆ιαµόρφωση (Modulation)<br />
FT<br />
f() t ↔ F( ω)<br />
FT<br />
jω0t<br />
() ↔F( ω − ω0)<br />
f t e<br />
Απόδειξη<br />
∞<br />
∞<br />
− jω0t jω0t − j( ω−ω0)<br />
t<br />
{ () } = ∫ () = ∫ () = ( ω −ω0)<br />
−∞<br />
−∞<br />
FT f t e f t e dt f t e dt F<br />
∞<br />
jω0t − jω0t<br />
e + e − jωt<br />
FT[ x( t)cos ω0t] = ∫ x( t)<br />
e dt<br />
2<br />
−∞<br />
1 1<br />
xt ()cos ω0t↔ X( ω− ω0) + Χ ( ω+<br />
ω0)<br />
2 2<br />
Κλιµάκωση στον χρόνο (µικρή διάρκεια στον χρόνο,µεγάλη στη συχνότητα)<br />
1 ω<br />
f( at) ↔ F( )<br />
a α<br />
Προκύπτει ότι για a = − 1 είναι f( −t) ↔F( − ω)<br />
FT<br />
Συνέλιξη στον χρόνο<br />
Αν<br />
FT<br />
f () t ↔ F( ω)<br />
1 1<br />
FT<br />
f () t ↔ F ( ω)<br />
2 2<br />
FT<br />
Τότε f t = f1 t f2 t ↔ F = F1 F2<br />
() ()* () ( ω) ( ω) ( ω)<br />
30
Απόδειξη<br />
∞ ∞ ∞<br />
− jωt<br />
∫ 1 2 ∫ ∫ 1 2<br />
−∞ −∞ −∞<br />
− jωt<br />
FT[ f ( t)] = [ f ( t)* f ( t)] e dt = [ f ( τ) f ( t − τ) dτ]<br />
e dt =<br />
Αλλάζουµε την σειρά ολοκλήρωσης t µε τ:<br />
∞ ∞ ∞ ∞<br />
− jωt − jωτ − jωτ<br />
∫ 1 ∫ 2<br />
− = ∫ 1 2<br />
=<br />
2 ∫ 1<br />
=<br />
1<br />
-∞ −∞ −∞ −∞<br />
= f ( τ )[ f ( t τ) e dt] dτ f ( τ) F ( ω) e dτ F ( ω) f ( τ) e dτ F( ω)<br />
F<br />
F ( ω ) 1<br />
Μετασχηµατισµός FOURIER παραγώγου συνάρτησης<br />
FT<br />
Αν f() t ↔ F( ω)<br />
Τότε<br />
df () t<br />
FT<br />
↔ jωF( ω)<br />
και γενικά ισχύει:<br />
dt<br />
n<br />
d f()<br />
t<br />
FT<br />
n<br />
↔ ( jω) F( ω)<br />
dt<br />
∞<br />
df () t d 1<br />
jωt<br />
= [ F( ω) e dω]<br />
=<br />
dt dt 2π<br />
∫<br />
−∞<br />
Απόδειξη<br />
Αλλαγ<br />
ή σειράς της παραγώγισης και ολοκλήρωσης:<br />
∞ ∞ ∞<br />
jωt<br />
1 de 1 jωt<br />
1<br />
jωt<br />
= F( ) d F( ) j e d [ j F( )] e d<br />
2π<br />
∫ ω ω = ω ω ω ω ω ω<br />
dt 2π<br />
∫ =<br />
2π<br />
∫<br />
−∞ −∞ −∞<br />
Εφαρµογή για την δ-Dirac:<br />
n<br />
FT{ δ ( t)} = ( jω)<br />
n<br />
∞<br />
1 2<br />
Σχέση Parseval∈= ∫ f () t dt = A ( ω)<br />
dω<br />
2π<br />
∫<br />
−∞<br />
2<br />
∞<br />
−∞<br />
31
ΑΣΚΗΣΗ<br />
Να υπολογιστεί η ενέργεια που βρίσκεται στην ζώνη συχνοτήτων απο ω = 0 εως<br />
−<br />
ω = 20 π ( rad)<br />
του σήµατος f () t = e t u()<br />
t . Επίσης το ποσοστό % της ενέργειας.<br />
Λύση<br />
1 1 jφω<br />
( ) −1<br />
F( ω) = = e , φω ( ) =−tan ( ω)<br />
1+ jω<br />
2<br />
ω + 1<br />
∞ ∞ −2t<br />
∞<br />
−t<br />
2 −2t<br />
e<br />
1<br />
∈= ∫[ e ] dt = ∫e dt = [ ] =<br />
−2 2<br />
0 0 0<br />
∞<br />
1 dω 1 −1<br />
∞ 1 π π 1<br />
[tan ω] ( )<br />
2<br />
2π ∫<br />
−∞<br />
ω + 1 2π 2π<br />
2 2 2<br />
−∞<br />
∈= = = + =<br />
Αρα ισχύει η ταυτότητα του Parseval<br />
20π<br />
dω<br />
−1 62.8<br />
1 ∫<br />
ω<br />
2<br />
−62.8<br />
+<br />
−20π<br />
∈<br />
1<br />
0.495 = = =<br />
1 1 1<br />
∈= = [tan ] = (1.55 + 1.55) = 0.495<br />
2π ω 1 2π 2π<br />
∈<br />
0.5<br />
0.99 99%<br />
32