grk, TMMI17, 2006-04-19 kl 14-18 DEL 1

Tekniska Högskolan i Linköping, IKP/Tore Dahlberg
TENTAMEN i Hållfasthetslära; grk, TMMI17, 2006-04-19 kl 14-18
DEL 1 - (Teoridel utan hjälpmedel)
LÖSNINGAR
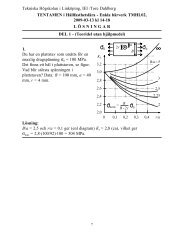
1. En dragstång (längd L, area A och elasticitetsmodul E) belastas med en
dragkraft P. Visa, med användande av jämviktssamband,
deformationssamband och materialsamband (Hookes lag), att stångens
längdändring blir
δ= PL
EA
Lösning:
Jämvikt ger
σ= P A
Deformationssamband
ε= δ L
Materialsamband (Hookes lag) ger
ε= σ E
Eliminera σ och ε. Det ger
δ=εL = σ E L = P A
L
E = PL
EA
6

2.
P
L, EI
Elementarfall: Konsolbalk
P
L, EI
x
z w(x)
En balk (längd L, böjstyvhet EI) är fast inspänd
i sin ena ände och slidlagrad i den andra, se
figur. Balken belastas med kraften P enligt
figur. Bestäm balkändens förskjutning δ.
w(x)= PL3
6EI
w(L)= PL3
3EI
⎛
⎜
⎝ 3 x 2
L − x 3 ⎞ ⎟⎠
2 L 3
w’(L)= PL2
2EI
z
L, EI
w(x)
M
x
w(x)= ML2
2EI
w(L)= ML2
2EI
⎛ x 2 ⎞
⎜ ⎟⎠
⎝ L 2
w’(L)= ML
EI
Lösning:
Balken får en inflektionspunkt i mitten, varför momentet där är noll och halva
balken kan ses som en konsolbalk belastad med kraften P. Symmetri i
utböjningen för den andra halva ger därmed
Altenativ lösning: Ta bort slidlagringen och lägg in ett moment M där.
Balkändens snedställnign blir då
Men Θ = 0 ger att M =
Utböjningen δ blir då
δ P (L / 2)3
=
2 3EI
− PL/2
som ger
Θ= PL2
2EI + ML
EI
δ= PL3
12EI
δ= PL3
3EI + ML2
2EI = PL3
3EI + − PL3 = PL3
4EI 12EI
7

Tekniska Högskolan i Linköping, IKP
Tore Dahlberg
TENTAMEN i Hållfasthetslära; grk, TMMI17, 2006-04-19 kl 14-18
DEL 1 - (Teoridel utan hjälpmedel)
P
3.
En rätvinklig triangulär plåt (sidor a och b, se
figur) hålls i läge (med sidorna vertikalt
a
respektive horisontellt) av en fjäder med styvhet
k enligt figur. Plåten belastas med en vertikal
b
kraft P enligt figur. Bestäm knäcklasten för
k
anordningen.
Lösning: Ge systemet en liten störning (en liten vinkel φ) och teckna
momentjämvikt. Utböjande moment blir M ut = P asin φ = Paφ
och det
återförande momentet blir M åt =(k bsin φ) (bcos φ) = k b φb 1 (där k bsinφ
är
fjäderkraft och bcosφ
är hävarm, och φ är en liten vinkel).
Jämvikt ger Paφ - kb 2 φ = 0, varur löses (villkor för att φ≠0) P = P krit = kb 2 /a.
4.
Huvudspänningarna i en punkt i ett material har bestämts till σ 1 = 300 MPa, σ 2
= 220 MPa och σ 3 = 100 MPa. Hur stor är effektivspänningen i punkten?
Lösning: Effektivspänningen är enligt Trescas hypotes
σ Tresca e
=σ hsp max
−σ hsp min
= 300 −(−100)=400 MPa
8

Tekniska Högskolan i Linköping, IKP
Tore Dahlberg
TENTAMEN i Hållfasthetslära; grk, TMMI17, 2006-04-19 kl 14-18
DEL 2 - (Problemdel med hjälpmedel)
elastiskt
område
plastiskt
område
R
R/2
s
5.
En axel (längd L, skjuvmodul G) med cirkulärt
tvärsnitt (radie R) belastas med ett vridande
moment M v så att en plastisk zon utbildas.
Området r > R / 2 har plasticerat, medan
området r < R / 2 fortfarande är elastiskt.
Materialet är linjärt elastiskt, idealplastiskt med
sträckgräns τ s i skjuvning. Destäm axeln
förvridningsvinkel vid denna
spänningsfördelning.
Lösning:
Vid radien r = R / 2 är skjuvspänningen τ s . För den centrala (elastiska) delen
gäller vid radien r = R / 2 att (se t ex läroboken Kap 9, ekv (2a,b) med dx = L)
Θ R 2 =γ s L
där Θ är axelns förvridning och γ s är skjuvningen då skjuvspänningen är τ s .
Med γ s = τ s /G erhålls
Θ= 2 τ s
R G L = 2 τ s L
RG
Momentet behöver alltså inte bestämmas!
9

Tekniska Högskolan i Linköping, IKP
Tore Dahlberg
TENTAMEN i Hållfasthetslära; grk, TMMI17, 2006-04-19 kl 14-18
DEL 2 - (Problemdel med hjälpmedel)
-
P
A
P
A
M
T
P
2L
B
3L
C
x
2L
B
3L
C
x
x
- 2 PL PL
P
x
6.
Bestäm moment- och tvärkraftsfördelning i
balken enligt figur. Rita upp både momentdiagrammet
och tvärkraftsdiagramet för fallet.
Lösning:
Snitta i 0 < x

Tekniska Högskolan i Linköping, IKP
Tore Dahlberg
TENTAMEN i Hållfasthetslära; grk, TMMI17, 2006-04-19 kl 14-18
DEL 2 - (Problemdel med hjälpmedel)
y
t = 1 mm
z
25 mm
25 mm
7.
En 1 mm tjock plåt bockas så att en balk med
tvärsnitt enligt figur erhålls. Balken belastas
med en kraft genom skjuvcentrum så att
tvärkraften T (= T z ) = 1000 N uppkommer.
Bestäm maximal skjuvspänning i balken.
25 mm
Lösning:
Skjuvspänningen bestäms med formeln
Maximal skjuvspänning erhålls vid y-axeln. Tvärsnittet är tunnväggigt. Man
får
Yttröghetsmomentet I blir
τ= TS A’
Ib
S A
’ = 25 ⋅ 1 ⋅ 25 + 25 ⋅ 1 ⋅ 12, 5 = 937, 5mm 3
I = 2 ⎛ 25 ⋅ 1 3
⎜ ⎝ 12 + 252 ⋅ 1 ⋅ 25 ⎞ ⎟ + 1 ⋅ 503 = 41 671 mm4
⎠ 12
och b = t = 1 mm. Det ger
τ=
1000 ⋅ 937, 5
41 671 ⋅ 1 = 22, 5N/mm2 = 22, 5 MPa
11

Tekniska Högskolan i Linköping, IKP
Tore Dahlberg
TENTAMEN i Hållfasthetslära; grk, TMMI17, 2006-04-19 kl 14-18
DEL 2 - (Problemdel med hjälpmedel)
L
E, A
P
8. Ett stångbärverk består av fem stänger enligt
figur. De bildar två trianglar med vinklar 30 o
(π/6), 60 o (π/3) och 90 o (π/2). Alla stänger har
samma E och A och längden av den längsta
stången är L. Den yttre knuten belastas med den
vertikala kraften P. Bestäm knutens vertikala
förskjutning på grund av lasten.
S3
som ger S 1 = √⎯3 P/2 och S 2 = − P/2.
Jämvikt för den övre knuten ger
som ger S 3 = − S 4 och S 4 = − S 1 .
Jämvikt för den slidlagrade knuten ger S 5 =0.
Teckna den upplagrade energin i bärverket. Man får
U =∑
Castiglianos sats ger
Lösning:
Bestäm först stångkrafterna. Vertikal respektive
horisontell jämvikt för den yttre knuten ger
S
S 1
S 4
5
1
P + S 2
2 − S 1
P
S2
5 Ni 2 L i
i = 1
√⎯3
2 = 0
√⎯3
S 2
2 + S 1
1
2 = 0
1
S 1
+ S 4
2 − S 1
3
2 = 0 och S √⎯3
4
2 + S √⎯3
3
2 = 0
2EA = P 2 L
2EA
⎧
⎨
⎩
3
4 ⋅ 1 2 + 1 4 ⋅ √⎯ 3
2 + 3 4 ⋅ 1 2 + 3 4 ⋅ 1 + 0⎫ ⎬ = P 2 L
⎭ 2EA
δ= dU
dP = PL
EA
⎧
⎨
⎩
√⎯3 + 12
8
⎫
⎬
⎭
= 1, 72
PL
EA
⎧
⎨
⎩
√⎯3 + 12
8
⎫
⎬
⎭
12