KAPITEL 4. Lineare Ausgleichsrechnung Beispiel 4.1. Das ...
KAPITEL 4. Lineare Ausgleichsrechnung Beispiel 4.1. Das ...
KAPITEL 4. Lineare Ausgleichsrechnung Beispiel 4.1. Das ...
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
<strong>KAPITEL</strong> <strong>4.</strong> <strong>Lineare</strong> <strong>Ausgleichsrechnung</strong><br />
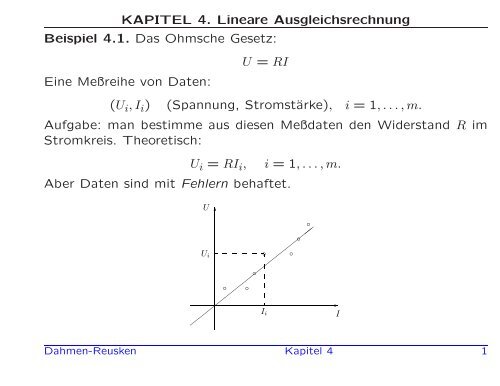
<strong>Beispiel</strong> <strong>4.</strong>1. <strong>Das</strong> Ohmsche Gesetz:<br />
Eine Meßreihe von Daten:<br />
U = RI<br />
(U i , I i ) (Spannung, Stromstärke), i = 1, . . . , m.<br />
Aufgabe: man bestimme aus diesen Meßdaten den Widerstand R im<br />
Stromkreis. Theoretisch:<br />
U i = RI i , i = 1, . . . , m.<br />
Aber Daten sind mit Fehlern behaftet.<br />
U<br />
✻<br />
❜<br />
❜<br />
★<br />
U i<br />
❜ ❜<br />
❜<br />
❜ ❜<br />
★ ★★★★★★★★★★★★ I i<br />
✲<br />
I<br />
Dahmen-Reusken Kapitel 4 1
Man kann hierzu versuchen, die durch eine Wahl von R bedingten<br />
Residuen U i − RI i zu quadrieren, aufzusummieren und dasjenige R zu<br />
suchen, das diesen Ausdruck minimiert:<br />
f(R) :=<br />
m∑<br />
i=1<br />
(RI i − U i ) 2 = min .<br />
Da f eine quadratische Funktion ist, kann nur ein Extremum vorliegen,<br />
das durch die Nullstelle der Ableitung gegeben ist:<br />
0 = f ′ (R) =<br />
m∑<br />
i=1<br />
( ∑ m<br />
2(RI i − U i )I i = 2R Ii<br />
2<br />
i=1<br />
Hier ergibt sich diese Nullstelle R ∗ als<br />
)<br />
− 2<br />
m∑<br />
i=1<br />
U i I i .<br />
R ∗ =<br />
( ∑ m<br />
i=1<br />
U i I i<br />
)/( m ∑<br />
Ii<br />
2<br />
i=1<br />
)<br />
. △<br />
Dahmen-Reusken Kapitel 4 2
<strong>Beispiel</strong> <strong>4.</strong>2.<br />
In der Fourieranalyse wird eine T-periodische Funktion f durch eine<br />
Linearkombination der T-periodischen trigonometrischen Polynome<br />
1, cos(ct), sin(ct), cos(2ct), sin(2ct), . . . , cos(Nct), sin(Nct)<br />
mit c := 2π<br />
T<br />
in der Form<br />
approximiert.<br />
g N (t) = 1 2 a 0 +<br />
N∑<br />
k=1<br />
(a k cos(kct) + b k sin(kct)) ,<br />
Annahme: nicht f, sondern nur eine Reihe von Meßdaten<br />
b i ≈ f(t i ), 0 ≤ t 1 < t 2 < . . . < t m ≤ T,<br />
ist bekannt, wobei m > 2N + 1.<br />
Ansatz zur Bestimmung der Koeffizienten a 0 , a 1 , b 1 , a 2 , b 2 , . . . , a N , b N :<br />
m∑<br />
i=1<br />
(g N (t i ) − b i ) 2 = min . △<br />
Dahmen-Reusken Kapitel 4 3
<strong>Das</strong> allgemeine lineare Ausgleichsproblem<br />
<strong>Das</strong> Minimierungsproblem<br />
m∑<br />
i=1<br />
(y(t i ; x 1 , . . . , x n ) − b i ) 2 =<br />
m∑<br />
i=1<br />
(a i,1 x 1 + . . . + a i,n x n − b i ) 2 = min<br />
wird in Matrixform dargestellt. Setzt man<br />
A = (a i,j ) m,n<br />
i,j=1 ∈ Rm×n , b ∈ R m ,<br />
nimmt das Minimierungsproblem eine kompakte Form an:<br />
Also:<br />
‖Ax − b‖ 2 2 = min<br />
x∈R n .<br />
Zu gegebenem A ∈ R m×n und b ∈ R n , bestimme x ∗ ∈ R n , für das<br />
gilt.<br />
‖Ax ∗ − b‖ 2 = min<br />
x∈R n ‖Ax − b‖ 2<br />
Dahmen-Reusken Kapitel 4 4
<strong>Beispiel</strong> <strong>4.</strong>3.<br />
Man vermutet, daß die Meßdaten<br />
einer Gesetzmäßigkeit der Form<br />
t 0 1 2 3<br />
y 3 2.14 1.86 1.72<br />
y = f(t) = α 1<br />
1 + t + β<br />
mit noch zu bestimmenden Parametern α, β ∈ R gehorchen. <strong>Das</strong> zugehörige<br />
lineare Ausgleichsproblem hat die Gestalt (<strong>4.</strong>14), mit<br />
x =<br />
(<br />
α<br />
β)<br />
, A =<br />
⎛ ⎞<br />
1 1<br />
1 2<br />
1<br />
⎜1<br />
⎝3 1<br />
⎟<br />
⎠<br />
1<br />
4 1<br />
, b =<br />
⎛<br />
⎜<br />
⎝<br />
3<br />
2.14<br />
1.86<br />
1.72<br />
⎞<br />
⎟<br />
⎠ .<br />
△<br />
Dahmen-Reusken Kapitel 4 5
Normalgleichungen<br />
Die Lösung von (<strong>4.</strong>14) läßt sich auf die Lösung des linearen Gleichungssystems<br />
A T Ax = A T b<br />
reduzieren, das häufig als Normalgleichungen bezeichnet wird.<br />
Beachte: für A ∈ R m×n ist die Matrix A T A ∈ R n×n stets quadratisch.<br />
Kernaussage:<br />
Satz <strong>4.</strong>5. x ∗ ∈ R n ist genau dann Lösung des linearen Ausgleichsproblems<br />
(<strong>4.</strong>14), wenn x ∗ Lösung der Normalgleichungen<br />
A T Ax = A T b<br />
ist. <strong>Das</strong> System der Normalgleichungen hat stets mindestens eine<br />
Lösung. Sie ist genau dann eindeutig, wenn Rang(A) = n gilt.<br />
Dahmen-Reusken Kapitel 4 6
Geometrische Interpretation<br />
Anschaulich ist klar, daß die Differenz b − Ax gerade senkrecht auf<br />
dem Bildraum Bild(A) = {Ax | x ∈ R n } stehen muß, damit der Abstand<br />
‖Ax − b‖ 2 minimal ist. Also gilt:<br />
‖Ax − b‖ 2 = min ⇐⇒ Ax − b ⊥ Bild(A) ,<br />
✻<br />
R m−n<br />
✒<br />
b ❅<br />
❅<br />
❅<br />
✁ ✁✁✁✁✁✕<br />
✒ Ax ∗<br />
b − Ax ∗<br />
❅■<br />
❅<br />
❅✁ ✁✁✁✁✁✁ x ∗ ∈ R n<br />
<br />
Bild(A)<br />
= {Ax | x ∈ R n }<br />
✲<br />
R n<br />
Dahmen-Reusken Kapitel 4 7
In <strong>Beispiel</strong> 3.32 wurde bereits folgende Tatsache gezeigt:<br />
Bemerkung <strong>4.</strong>6. Falls A ∈ R m×n vollen (Spalten-)Rang n hat,<br />
so ist die Matrix A T A ∈ R n×n symmetrisch positiv definit.<br />
Annahme: Wir beschränken uns in den Abschnitten <strong>4.</strong>3 und <strong>4.</strong>4 auf<br />
den Fall, daß A vollen Spaltenrang hat: Rang(A) = n.<br />
Der Fall Rang(A) < n wird in Abschnitt <strong>4.</strong>7 diskutiert.<br />
Dahmen-Reusken Kapitel 4 8
Kondition des linearen Ausgleichsproblems<br />
κ 2 (A) := max<br />
x≠0<br />
Ausgleichsproblem mit Störungen:<br />
/<br />
‖Ax‖ 2<br />
min<br />
‖x‖ 2 x≠0<br />
‖A˜x −˜b‖ 2 = min .<br />
‖Ax‖ 2<br />
‖x‖ 2<br />
.<br />
❍ ❍❍❍❍❥<br />
δb<br />
˜b<br />
b<br />
✟ ✟✟✟✟✟✟✟✟✟✟✟✟✟✟✟✟✯<br />
✒❍ Θ Ax ∗ A˜x<br />
✲ ✲<br />
Satz <strong>4.</strong>7. Für die Kondition des linearen Ausgleichsproblems<br />
bezüglich Störungen in b gilt<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≤ κ 2(A) ‖˜b − b‖ 2<br />
.<br />
cosΘ ‖b‖ 2<br />
Dahmen-Reusken Kapitel 4 9
A :=<br />
⎛<br />
⎜<br />
⎝<br />
<strong>Beispiel</strong> <strong>4.</strong>8.<br />
⎞<br />
1 1<br />
⎟<br />
0 0⎠ , b :=<br />
0 1<br />
⎛<br />
⎜<br />
⎝<br />
0.01<br />
1<br />
0<br />
⎞<br />
⎟<br />
⎠ .<br />
Man kann einfach nachrechnen, daß κ 2 (A) ≈ 2.62 und<br />
( )<br />
x ∗ = (A T A) −1 A T 0.01<br />
b =<br />
0<br />
gilt. Für ˜b = (0.01,1,0.01) T erhält man<br />
Daraus folgt<br />
˜x = (A T A) −1 A T˜b =<br />
( )<br />
0<br />
.<br />
0.01<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≈ 100 ‖˜b − b‖ 2<br />
‖b‖ 2<br />
,<br />
also eine schlechte Kondition. Es gilt<br />
cosΘ = ‖Ax∗ ‖ 2<br />
‖b‖ 2<br />
= 0.01. △<br />
Dahmen-Reusken Kapitel 4 10
Kondition des linearen Ausgleichsproblems<br />
Satz <strong>4.</strong>9. Für die Kondition des linearen Ausgleichsproblems<br />
bezüglich Störungen in A gilt<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≤ ( κ 2 (A) + κ 2 (A) 2 tanΘ ) ‖Ã − A‖ 2<br />
‖A‖ 2<br />
.<br />
Dahmen-Reusken Kapitel 4 11
Numerische Lösung des linearen Ausgleichsproblems<br />
Lösung der Normalgleichungen<br />
Die Matrix A T A ist symmetrisch positiv definit.<br />
Folglich ergibt sich die Methode:<br />
• Berechne A T A, A T b.<br />
• Berechne die Cholesky-Zerlegung<br />
von A T A.<br />
• Löse<br />
LDL T = A T A<br />
Ly = A T b,<br />
L T x = D −1 y<br />
durch Vorwärts- bzw. Rückwärtseinsetzen.<br />
Dahmen-Reusken Kapitel 4 12
Nachteile dieser Vorgehensweise<br />
• Die Berechnung von A T A ist für große m aufwendig und birgt<br />
die Gefahr von Genauigkeitsverlust durch Auslöschungseffekte. Die<br />
Einträge von A T A sind also mit (möglicherweise erheblichen relativen)<br />
Fehlern behaftet.<br />
• Bei der Lösung des Systems A T Ax = A T b über das Cholesky-<br />
Verfahren werden die Rundungsfehler in A T A und A T b mit<br />
verstärkt. Es gilt<br />
κ 2 (A T A)<br />
κ 2 (A T A) = κ 2 (A) 2 .<br />
Folglich wird die Rundungsfehlerverstärkung durch κ 2 (A) 2 beschrieben.<br />
Dahmen-Reusken Kapitel 4 13
<strong>Beispiel</strong> <strong>4.</strong>12.<br />
A =<br />
⎛<br />
⎜<br />
⎝<br />
√ √<br />
3 3<br />
δ 0<br />
0 δ<br />
⎞<br />
⎟<br />
⎠ , b =<br />
⎛<br />
⎜<br />
⎝<br />
⎞<br />
2 √ 3<br />
⎟<br />
δ ⎠ , 0 < δ ≪ 1.<br />
δ<br />
<strong>Das</strong> lineare Ausgleichsproblem ‖Ax − b‖ 2 = min hat die Lösung<br />
x ∗ = (1,1) T (für alle δ > 0). Außerdem gilt Θ = 0.<br />
Daher wird die Kondition dieses Problems durch κ 2 (A) beschrieben.<br />
Man rechnet einfach nach, daß<br />
√<br />
6<br />
κ 2 (A) ≈<br />
δ<br />
gilt. Ein stabiles Verfahren sollte ein Resultat ˜x liefern, mit<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
κ 2 (A) eps .<br />
Dahmen-Reusken Kapitel 4 14
Die Lösung dieses Problems über die Normalgleichungen und das<br />
Cholesky-Verfahren auf einer Maschine mit eps ≈ 10 −16 ergibt:<br />
δ = 10 −4 :<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≈ 2 ∗ 10 −8 ≈ 1 3 κ 2(A) 2 eps<br />
δ = 10 −6 :<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≈ 2 ∗ 10 −4 ≈ 1 3 κ 2(A) 2 eps .<br />
Dahmen-Reusken Kapitel 4 15
Lösung über QR-Zerlegung<br />
Satz <strong>4.</strong>13. Sei A ∈ R m×n mit Rang(A) = n und b ∈ R m . Sei<br />
Q ∈ R m×m eine orthogonale Matrix und ˜R ∈ R n×n eine obere<br />
Dreiecksmatrix, so daß<br />
QA = R :=<br />
) (˜R } n<br />
∅ } m − n .<br />
Dann ist die Matrix ˜R regulär. Schreibt man<br />
Qb =<br />
(<br />
b1<br />
b 2<br />
)<br />
} n<br />
} m − n ,<br />
dann ist x ∗ = ˜R −1 b 1 die Lösung des linearen Ausgleichsproblems<br />
(<strong>4.</strong>14). Die Norm ‖Ax ∗ − b‖ 2 ist gerade durch ‖b 2 ‖ 2 gegeben.<br />
Grundidee:<br />
‖Ax − b‖ 2 2 = ‖QAx − Qb‖2 2 = ‖Rx − Qb‖2 2 = ‖˜Rx − b 1 ‖ 2 2 + ‖b 2‖ 2 2 .<br />
Dahmen-Reusken Kapitel 4 16
Aus Satz <strong>4.</strong>13 ergibt sich nun folgende Methode:<br />
• Bestimme von A die QR-Zerlegung<br />
) (˜R<br />
QA = (˜R ∈ R n×n ),<br />
∅<br />
z.B. mittels Givens-Rotationen oder Householder-Spiegelungen<br />
und berechne Qb = ( b 1<br />
b2<br />
)<br />
.<br />
• Löse<br />
mittels Rückwärtseinsetzen.<br />
˜Rx = b 1<br />
Die Norm des Residuums min x∈R n ‖Ax − b‖ 2 = ‖Ax ∗ − b‖ 2 ist gerade<br />
durch ‖b 2 ‖ 2 gegeben.<br />
Dahmen-Reusken Kapitel 4 17
<strong>Beispiel</strong> <strong>4.</strong>15.<br />
Sei<br />
A =<br />
⎛<br />
⎜<br />
⎝<br />
⎞<br />
3 7<br />
⎟<br />
0 12⎠ , b =<br />
4 1<br />
⎛<br />
⎜<br />
⎝<br />
10<br />
1<br />
5<br />
⎞<br />
⎟<br />
⎠ ,<br />
d.h. m = 3, n = 2. Man bestimme die Lösung x ∗ ∈ R 2 von<br />
‖Ax − b‖ 2 = min .<br />
• Annullierung von a 3,1 :<br />
A (2) = G 1,3 A =<br />
⎛<br />
⎜<br />
⎝<br />
⎞<br />
5 5<br />
⎟<br />
0 12⎠ , b (2) = G 1,3 b =<br />
0 −5<br />
(In der Praxis werden die Transformationen G 1,3 A und G 1,3 b ausgeführt,<br />
ohne daß G 1,3 explizit berechnet wird.)<br />
⎛<br />
⎜<br />
⎝<br />
10<br />
1<br />
−5<br />
⎞<br />
⎟<br />
⎠ .<br />
Dahmen-Reusken Kapitel 4 18
• Annullierung von a (2)<br />
3,2 :<br />
A (3) = G 2,3 A (2) =<br />
⎛<br />
⎜<br />
⎝<br />
5 5<br />
0 13<br />
0 0<br />
⎞<br />
⎟<br />
⎠ =<br />
Lösung von<br />
( )<br />
5 5<br />
( x ) ( 1 10)<br />
=<br />
0 13 x<br />
37 2 13<br />
durch Rückwärtseinsetzen:<br />
(<br />
x ∗ 301<br />
=<br />
169 , 37 ) T<br />
.<br />
169<br />
) (˜R<br />
, b (3) = G<br />
∅ 2,3 b (2) =<br />
⎛<br />
⎜<br />
⎝<br />
⎞<br />
10<br />
37<br />
13<br />
⎟<br />
− 55 ⎠ .<br />
13<br />
Als Norm des Residuums ergibt sich:<br />
‖b 2 ‖ 2 = 55<br />
13 . △<br />
Dahmen-Reusken Kapitel 4 19
Wegen Satz 3.41 gilt<br />
κ 2 (A) = κ 2 (˜R),<br />
d.h., das Quadrieren der Kondition, das bei den Normalgleichungen<br />
auftritt, wird vermieden. Außerdem ist die Berechnung der<br />
QR-Zerlegung über Givens- oder Householder-Transformationen<br />
ein sehr stabiles Verfahren, wobei die Fehlerverstärkung durch<br />
κ 2 (A) (und nicht κ 2 (A) 2 ) beschrieben wird.<br />
Dahmen-Reusken Kapitel 4 20
<strong>Beispiel</strong> <strong>4.</strong>16<br />
Wir nehmen A und b wie in <strong>Beispiel</strong> <strong>4.</strong>12. Die Methode über die QR-<br />
Zerlegung von A, auf einer Maschine mit eps ≈ 10 −16 , ergibt<br />
δ = 10 −4 :<br />
δ = 10 −6 :<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≈ 2.2 ∗ 10 −16 ,<br />
‖˜x − x ∗ ‖ 2<br />
‖x ∗ ‖ 2<br />
≈ 1.6 ∗ 10 −16 .<br />
Wegen der sehr guten Stabilität dieser Methode sind diese Resultate<br />
viel besser als die Resultate in <strong>Beispiel</strong> <strong>4.</strong>12.<br />
△<br />
Dahmen-Reusken Kapitel 4 21
<strong>4.</strong>5 Zum statistischen Hintergrund - lineare Regression<br />
Gegeben seien Daten (t 1 , y 1 ), . . . ,(t m , y m ) mit<br />
t i : feste (deterministische) Meßpunkte,<br />
y i : Realisierungen von Zufallsvariablen Y i .<br />
<strong>Lineare</strong> Regression basiert auf dem Ansatz<br />
Y i =<br />
n∑<br />
k=1<br />
a k (t): geeignete Ansatzfunktionen,<br />
F i : Meßfehler (Zufallsvariablen).<br />
a k (t i )x k + F i , i = 1, . . . , m,<br />
Ziel: eine Schätzung ˆx = (ˆx 1 , . . . ,ˆx n ) T für den unbekannten Parametersatz<br />
x = (x 1 , . . . , x n ) T ∈ R n bestimmen.<br />
Einen solchen Schätzer liefert die lineare <strong>Ausgleichsrechnung</strong>.<br />
Sei nämlich ˆx die Lösung des linearen Ausgleichsproblems<br />
‖Ax − y‖ 2 2 → min .<br />
Dann ist ˆx ebenfalls eine Zufallsvariable.<br />
Dahmen-Reusken Kapitel 4 22
ˆx als Best Linear Unbiased Estimator (BLUE)<br />
Annahmen:<br />
- F i unabhängig, identisch verteilt mit Erwartungswert E(F i ) = 0<br />
- Varianz-Kovarianzmatrix<br />
Dann gilt<br />
V (F) := E(FF T ) = ( E(F i F j ) ) m<br />
i,j=1 = σ2 I<br />
E(ˆx) = x, V (ˆx) = E ( (ˆx − x)(ˆx − x) T ) = σ 2 (A T A) −1 .<br />
Der Schätzer ist erwartungstreu und hat minimale Varianz.<br />
Man spricht von einem Best Linear Unbiased Estimator (BLUE).<br />
Dahmen-Reusken Kapitel 4 23
ˆx als Maximum-Likelihood-Schätzer<br />
Annahmen:<br />
- F i unabhängig, identisch verteilt mit Erwartungswert 0<br />
- Varianz-Kovarianzmatrix V (F) = σ 2 I<br />
- F i normalverteilt<br />
⇒: Y i normalverteilt, E(Y ) = Ax, V (Y ) = σ 2 I. Dichtefunktion von Y i :<br />
( z−(Ax)i<br />
σ<br />
f i (z) = 1<br />
σ √ 2π e−1 2<br />
Für die Meßreihe y 1 , . . . , y m ist die Likelihood-Funktion definiert durch<br />
L(x; y 1 , . . . , y m ) :=<br />
m∏<br />
i=1<br />
f i (y i ) =<br />
) 2<br />
.<br />
( 1<br />
2πσ 2 )m<br />
2<br />
e<br />
− 1<br />
2σ 2‖y−Ax‖22 .<br />
Ein Parameterwert ˜x heißt Maximum-Likelihood-Schätzwert, wenn<br />
L(˜x; y 1 , . . . , y m ) ≥ L(x; y 1 , . . . , y m )<br />
für alle x ∈ R n<br />
Der Maximum-Likelihood-Schätzer ist gerade der Schätzer ˆx aus dem<br />
linearen Ausgleichsproblem, weil<br />
‖y − A˜x‖ 2 = min<br />
x∈R n ‖y − Ax‖ 2.<br />
Dahmen-Reusken Kapitel 4 24
<strong>4.</strong>6 Orthogonale Projektion auf einem Teilraum<br />
Gegeben: ein Vektorraum V über R mit einem Skalarprodukt 〈·, ·〉.<br />
Durch ‖v‖ := 〈v, v〉 1 2 wird eine Norm auf V definiert.<br />
Aufgabe. Sei U ⊂ V ein n-dimensionaler Teilraum von V .<br />
Zu v ∈ V bestimme u ∗ ∈ U, für das<br />
gilt.<br />
‖u ∗ − v‖ = min<br />
u∈U<br />
‖u − v‖<br />
Im Falle des linearen Ausgleichsproblems ist U = Bild(A), A ∈ R m×n ,<br />
V = R m , 〈u, v〉 = ∑ m<br />
j=1 u j v j , D.h. ‖ · ‖ = ‖ · ‖ 2 .<br />
Bemerkung <strong>4.</strong>18. Weil U ein endlich-dimensionaler Teilraum ist, existiert<br />
ein Element in U mit minimalem Abstand zu v, d.h. es existiert<br />
u ∗ ∈ U, für das ‖u ∗ − v‖ = min u∈U ‖u − v‖ gilt.<br />
△<br />
Dahmen-Reusken Kapitel 4 25
Satz <strong>4.</strong>20. Unter den Bedingungen von Aufgabe <strong>4.</strong>17 existiert ein<br />
eindeutiges u ∗ ∈ U, das<br />
‖u ∗ − v‖ = min ‖u − v‖<br />
u∈U<br />
erfüllt. Ferner gilt das genau dann, wenn<br />
〈u ∗ − v, u〉 = 0 ∀u ∈ U,<br />
d.h. , u ∗ − v senkrecht (bzgl. 〈·, ·〉) zu U ist.<br />
u ∗ ist somit die orthogonale Projektion (bzgl. 〈·, ·〉) von v auf U.<br />
Die Lösung der Aufgabe <strong>4.</strong>17 ist also die orthogonale Projektion<br />
(bzgl. 〈·, ·〉) von v auf den Unterraum U.<br />
v<br />
U<br />
<br />
✡ ✡✡✡✡✡✡✡✡✣<br />
✲<br />
u ∗<br />
<br />
Dahmen-Reusken Kapitel 4 26
Eigenschaften der Projektion<br />
Zu v ∈ V existiert ein eindeutiges P U (v) ∈ U, so daß v − P U (v) ⊥ U,<br />
d.h. , 〈v − P U (v), u〉 = 0 ∀ u ∈ U.<br />
Mit P U : V → U ist also eine wohldefinierte Abbildung gegeben.<br />
(i) Die Abbildung P U : V → U ist linear.<br />
(ii) P U ist ein Projektor, d.h. P U (u) = u für alle u ∈ U (P 2 U = P U).<br />
(iii) Die Abbildung P U ist symmetrisch,<br />
d.h. 〈P U (v), w〉 = 〈v, P U (w)〉, ∀ v, w ∈ V.<br />
(iv) P U is beschränkt und zwar gilt ‖P U ‖ = sup ‖v‖=1 ‖P U (v)‖ = 1.<br />
Dahmen-Reusken Kapitel 4 27
Wie kann man P U (v) berechnen?<br />
Sei {φ 1 , . . . , φ n } eine Basis für U. Dann hat û = P U (v) eine eindeutige<br />
Darstellung<br />
P U (v) =<br />
n∑<br />
j=1<br />
c j φ j<br />
mit gewissen Koeffizienten c j = c j (v). Es gilt<br />
0 = 〈v − P U (v), φ k 〉 = 〈v, φ k 〉 −<br />
n∑<br />
j=1<br />
Definiert man die Gram-Matrix G := ( 〈φ k , φ j 〉 ) n<br />
c j 〈φ j , φ k 〉, k = 1, . . . , n.<br />
j,k=1<br />
c = (c 1 , . . . , c n ) T , v = (〈v, φ 1 〉, . . . , 〈v, φ n 〉) T so ergibt sich<br />
Gc = v<br />
und die Vektoren<br />
Die Berechnung einer orthogonalen Projektion läuft also im<br />
allgemeinen auf die Lösung eines symmetrisch positiv definiten<br />
Gleichungssystems hinaus.<br />
Dahmen-Reusken Kapitel 4 28
<strong>4.</strong>7 Singulärwertzerlegung (SVD) und Pseudoinverse<br />
Wir definieren die Lösungsmenge<br />
L(b) := {x ∈ R n | x ist Lösung des linearen Ausgleichproblems}<br />
Lemma <strong>4.</strong>2<strong>4.</strong> Die Lösungsmenge L(b) hat folgende Eigenschaften:<br />
(i) Es existiert ein eindeutiges x ∗ ∈ R n , so daß x ∗ = L(b) ∩Kern(A) ⊥ ,<br />
wobei Kern(A) ⊥ := {z ∈ R n | y T z = 0 , ∀ y ∈ Kern(A)}.<br />
(ii) Für alle x ∈ L(b) \ {x ∗ } gilt ‖x‖ 2 > ‖x ∗ ‖ 2 , d.h., x ∗ hat die kleinste<br />
Euklidische Norm in L(b).<br />
Folgerung <strong>4.</strong>25. Sei b ∈ R m , A ∈ R m×n . Die Aufgabe<br />
⎧<br />
⎨<br />
⎩<br />
bestimme x ∗ mit minimaler Euklidischer Norm,<br />
für das ‖Ax ∗ − b‖ 2 = min x∈R n ‖Ax − b‖ 2 gilt,<br />
hat eine eindeutige Lösung.<br />
Dahmen-Reusken Kapitel 4 29
Singulärwertzerlegung<br />
Satz <strong>4.</strong>27. Zu jeder Matrix A ∈ R m×n existieren orthogonale<br />
Matrizen U ∈ R m×m , V ∈ R n×n und eine Diagonalmatrix<br />
mit<br />
so daß<br />
Σ := diag(σ 1 , . . . , σ p ) ∈ R m×n , p = min{m, n} ,<br />
σ 1 ≥ σ 2 ≥ . . . ≥ σ p ≥ 0,<br />
U T AV = Σ.<br />
Die σ i heißen Singulärwerte von A (singular values). Die Spalten der<br />
Matrizen U, V nennt man die Links- bzw.Rechtssingulärvektoren.<br />
Dahmen-Reusken Kapitel 4 30
Pseudoinverse<br />
Satz <strong>4.</strong>28. Sei U T AV = Σ eine Singulärwertzerlegung von<br />
A ∈ R m×n mit Singulärwerten<br />
σ 1 ≥ . . . ≥ σ r > σ r+1 = . . . = σ p = 0, p = min{m, n}.<br />
Definiere A + ∈ R n×m durch<br />
A + = V Σ + U T<br />
mit<br />
Σ + = diag(σ −1<br />
1 , . . . , σ−1 r ,0, . . . ,0) ∈ R n×m .<br />
Dann ist A + b = x ∗ die Lösung des allgemeinen linearen<br />
Ausgleichproblems.<br />
A + heißt Pseudoinverse von A.<br />
Dahmen-Reusken Kapitel 4 31
Lemma <strong>4.</strong>29. Sei U T AV = Σ eine Singulärwertzerlegung von A mit<br />
Singulärwerten σ 1 ≥ . . . ≥ σ r > σ r+1 = . . . = σ p = 0, p = min{m, n}.<br />
Die Spalten der Matrizen U und V werden mit u i bzw. v i notiert.<br />
Dann gilt:<br />
(i) Av i = σ i u i , A T u i = σ i v i , i = 1, . . . , p.<br />
(ii) Rang(A) = r.<br />
(iii) Bild(A) = span{u 1 , . . . , u r }, Kern(A) = span{v r+1 , . . . , v n }.<br />
(iv) ‖A‖ 2 = σ 1 .<br />
(v) Sei κ ∗ 2 (A) := ‖A‖ 2‖A + ‖ 2 = σ 1<br />
σ r<br />
. Falls Rang(A) = n ≤ m, so gilt<br />
(vi) { σ i | i = 1, . . . , r} = {<br />
κ ∗ 2 (A) = κ 2(A) = max ‖x‖ 2 =1 ‖Ax‖ 2<br />
min ‖x‖2 =1 ‖Ax‖ 2<br />
√<br />
λ i (A T A) | i = 1, . . . , n } \ {0} .<br />
Dahmen-Reusken Kapitel 4 32
Abb. <strong>4.</strong>6. Orthogonale Basis in R n und R m<br />
R n<br />
R m<br />
span{v r+1 , . . . , v n }<br />
❇❇▼ = Kern(A)<br />
❇<br />
❇<br />
❇<br />
❇<br />
❇<br />
✏✶<br />
❇✏<br />
✏✏✏✏✏ span{v 1 , . . . , v r }<br />
0 = Bild(A T )<br />
A ✛ ✲<br />
A T<br />
span{u r+1 , . . . , u m }<br />
= Kern(A T )<br />
. .<br />
✂ ✂✂✂✂✂✂✂✍<br />
<br />
0 <br />
span{u 1 , . . . , u r }<br />
= Bild(A)<br />
Dahmen-Reusken Kapitel 4 33
Abb. <strong>4.</strong>7. Geometrische Interpretation der Singulärwertzerlegung<br />
R m<br />
R n<br />
v i<br />
❇❇▼<br />
❇<br />
❇ x<br />
.<br />
❇ ✒<br />
.<br />
.<br />
.<br />
. .<br />
.<br />
❇<br />
. ✏✶<br />
v T ❇<br />
i x v j<br />
.. .<br />
❇<br />
✏ .<br />
.<br />
.<br />
✏✏✏✏✏ . .<br />
vj T ..<br />
x<br />
A ✲<br />
. .<br />
.<br />
u i<br />
.<br />
.<br />
. Ax<br />
σ i vi Tx ✟✯.<br />
... .<br />
✂ ✂✂✂✂✂✂✂✍<br />
.<br />
✟ ✟✟✟✟✟ <br />
σ j vj Tx<br />
<br />
u j<br />
.<br />
.<br />
.<br />
.<br />
<br />
.<br />
.<br />
. .<br />
.<br />
.<br />
.<br />
.<br />
.<br />
Dahmen-Reusken Kapitel 4 34
<strong>4.</strong>7.1 Berechnung von Singulärwerten<br />
Lemma <strong>4.</strong>30. Sei A ∈ R m×n , und seien Q 1 ∈ R m×m , Q 2 ∈ R n×n<br />
orthogonale Matrizen. Dann haben A und Q 1 AQ 2 die gleichen Singulärwerte.<br />
Transformation auf Bidiagonalgestalt; <strong>Beispiel</strong>:<br />
Eine Householder-Transformation Q 1 , so daß<br />
Q 1 A =<br />
⎛<br />
⎜<br />
⎝<br />
∗ ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
⎞<br />
⎟<br />
⎠<br />
(<br />
∗ v<br />
T<br />
= 1<br />
∅ ∗<br />
)<br />
Dahmen-Reusken Kapitel 4 35
Sei ˜Q 1 ∈ R 3×3 eine Householder-Transformation, so daß<br />
˜Q 1 v 1 = ( ∗ 0 0) T . Mit ˆQ 1 :=<br />
(<br />
∗ v<br />
T<br />
Q 1 AˆQ 1 = 1<br />
∅ ∗<br />
( )<br />
1 ∅<br />
∅ ˜Q 1<br />
) ( )<br />
1 ∅<br />
∅ ˜Q 1<br />
erhält man<br />
=<br />
⎛<br />
⎜<br />
⎝<br />
∗ ∗ 0 0<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ ∗<br />
Auf ähnliche Weise können Nulleinträge erzeugt werden in der 2. Spalte,<br />
2. Zeile, 3. Spalte und <strong>4.</strong> Spalte:<br />
⎛ ⎞<br />
⎛ ⎞<br />
∗ ∗ 0 0<br />
∗ ∗ 0 0<br />
0 ∗ ∗ ∗<br />
0 ∗ ∗ 0<br />
Q 1 AˆQ 1 → Q 2 Q 1 AˆQ 1 = ⎜0 0 ∗ ∗⎟<br />
⎝0 0 ∗ ∗⎠ → Q 2Q 1 AˆQ 1 ˆQ 2 = ⎜0 0 ∗ ∗⎟<br />
⎝0 0 ∗ ∗⎠<br />
0 0 ∗ ∗<br />
0 0 ∗ ∗<br />
⎛ ⎞<br />
⎛ ⎞<br />
∗ ∗ 0 0<br />
∗ ∗ 0 0<br />
0 ∗ ∗ 0<br />
0 ∗ ∗ 0<br />
→ Q 3 Q 2 Q 1 AˆQ 1 ˆQ 2 = ⎜0 0 ∗ ∗⎟<br />
⎝0 0 0 ∗⎠ → Q 4Q 3 Q 2 Q 1 AˆQ 1 ˆQ 2 = ⎜0 0 ∗ ∗⎟<br />
⎝0 0 0 ∗⎠ .<br />
0 0 0 ∗<br />
0 0 0 0<br />
Dahmen-Reusken Kapitel 4 36<br />
⎞<br />
⎟<br />
⎠<br />
.
Bemerkung <strong>4.</strong>31. Der Aufwand zur Berechnung der oberen Bidiagonalmatrix<br />
B in <strong>4.</strong>65 beträgt mn 2 + O(mn) Operationen.<br />
△<br />
Die Matrix A und die sich ergebende Bidiagonalmatrix B haben die<br />
gleichen Singulärwerte.<br />
Die Singulärwerte der Matrix A sind die Wurzeln der Eigenwerte der<br />
Tridiagonalmatrix B T B.<br />
Für die Berechnung der Eigenwerte dieser Matrix werden im allgemeinen<br />
sehr viel weniger arithmetische Operationen benötigt als für die<br />
Berechnung der Eigenwerte der (vollbesetzten) Matrix A T A.<br />
Dahmen-Reusken Kapitel 4 37
<strong>4.</strong>7.2 Rangbestimmung<br />
Lemma <strong>4.</strong>32. Sei U T AV = Σ eine Singulärwertzerlegung von A mit<br />
Singulärwerten σ 1 ≥ . . . ≥ σ r > σ r+1 = . . . = σ p = 0, p = min{m, n}.<br />
Für 0 ≤ k ≤ p − 1 gilt:<br />
min{ ‖A − B‖ 2 | B ∈ R m×n , Rang(B) ≤ k } = σ k+1 .<br />
Folgerung <strong>4.</strong>33. Für A und à = A + ∆A ∈ R m×n mit Singulärwerten<br />
σ 1 ≥ . . . ≥ σ p bzw. ˜σ 1 ≥ . . . ≥ ˜σ p , p = min{m, n}, gilt<br />
|σ k − ˜σ k |<br />
|σ 1 |<br />
≤ ‖∆A‖ 2<br />
‖A‖ 2<br />
, für k = 1, . . . , p.<br />
In diesem Sinne ist das Problem der Singulärwertbestimmung gut konditioniert.<br />
Dahmen-Reusken Kapitel 4 38
Der Numerische Rang<br />
Sei à = (ã i,j ) eine mit Rundungsfehlern behaftete Annäherung von A,<br />
wobei ã i,j = a i,j (1 + ǫ i,j ) mit |ǫ i,j | ≤ eps.<br />
Mit E := (a i,j ǫ i,j ) ∈ R m×n ergibt sich<br />
‖A − Ã‖ 2 = ‖E‖ 2 ≤ √ m‖E‖ ∞ ≤ √ m‖A‖ ∞ eps ≤ √ mn‖A‖ 2 eps .<br />
Deswegen definieren wir:<br />
BÃ(eps) := { C ∈ R m×n | ‖Ã − C‖ 2<br />
‖Ã‖ 2<br />
≤ √ mn eps } .<br />
Der numerische Rang Rang num (Ã) der Matrix à ist:<br />
Rang num (Ã) := min{Rang(B) | B ∈ BÃ(eps) } .<br />
Dieser numerische Rang hängt von der Maschinengenauigkeit eps ab.<br />
Dahmen-Reusken Kapitel 4 39
Bestimmung des numerischen Ranges:<br />
Seien ˜σ 1 ≥ . . . ≥ ˜σ p die Singulärwerte der Matrix Ã. Es gilt<br />
min<br />
Rang(B)≤k<br />
‖Ã − B‖ 2<br />
‖Ã‖ 2<br />
= ˜σ k+1<br />
˜σ 1<br />
, 1 ≤ k < p .<br />
Die Umgebung BÃ(eps) enthält also eine Matrix B mit Rang(B) = k<br />
genau dann, wenn ˜σ k+1 /˜σ 1 ≤ √ mn eps.<br />
Der numerische Rang der Matrix à ist deshalb:<br />
Rang num (Ã) = min{1 ≤ k ≤ p | ˜σ k+1 ≤ ˜σ 1<br />
√ mn eps }.<br />
Dahmen-Reusken Kapitel 4 40
<strong>4.</strong>3<strong>4.</strong> <strong>Beispiel</strong><br />
Wir betrachten die Matrizen<br />
A 1 =<br />
⎛<br />
1<br />
10<br />
2<br />
10<br />
⎜ 3<br />
⎝10<br />
4<br />
10<br />
⎞<br />
1<br />
3<br />
0<br />
2<br />
3<br />
3<br />
3<br />
3<br />
0⎟<br />
⎠<br />
4<br />
3<br />
7<br />
, A 2 = A 1 + 10 eps<br />
⎛<br />
⎜<br />
⎝<br />
1<br />
0<br />
0<br />
0<br />
⎞<br />
⎟<br />
⎠<br />
(<br />
1 0 0<br />
)<br />
,<br />
wobei eps ≈ 2 ∗ 10 −16 . Es gilt Rang(A 1 ) = 2, Rang(A 2 ) = 3 .<br />
Die berechneten Singulärwerte dieser Matrizen sind<br />
7.776, 1.082, 1.731 ∗ 10 −16 bzw. 7.776, 1.082, 2.001 ∗ 10 −15 .<br />
In beiden Fällen sind die drei berechneten Singulärwerte strikt positiv,<br />
jedoch gilt<br />
Rang num (A 1 ) = Rang num (A 2 ) = 2.<br />
In der Praxis würde man hieraus schließen, daß beide Matrizen den<br />
Rang 2 haben.<br />
△<br />
Dahmen-Reusken Kapitel 4 41