2x2 - IGT

Bestapproximation durch Orthogonalprojektion
§R2.3, S.1337
Bestapproximation durch Orthogonalprojektion
§R2.3, S.1338
V
v
v*
U
V
v
v*
U
Satz R2M (Gauß 1795, Bessel 1818)
Zu jedem Vektor v ∈ V existiert genau eine Bestapproximation in U,
also ein Vektor v ∗ ∈ U, der ‖v − v ∗ ‖ ≤ ‖v − u‖ für alle u ∈ U erfüllt.
Sei e 1 , . . . , e n eine Orthonormalbasis des Unterraumes U.
Dann ist v ∗ gegeben durch die Orthogonalprojektion von v auf U:
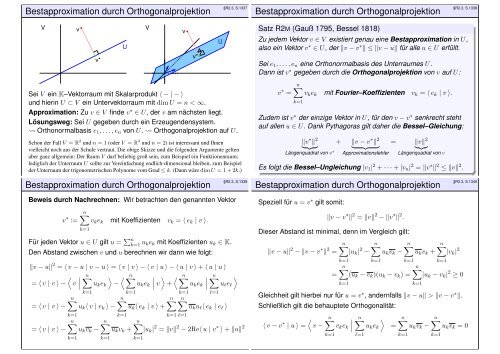
Sei V ein K–Vektorraum mit Skalarprodukt 〈 − | − 〉
und hierin U ⊂ V ein Untervektorraum mit dim U = n < ∞.
Approximation: Zu v ∈ V finde v ∗ ∈ U, der v am nächsten liegt.
Lösungsweg: Sei U gegeben durch ein Erzeugendensystem.
Orthonormalbasis e 1 , . . . , e n von U. Orthogonalprojektion auf U.
Schon der Fall V = R 2 und n = 1 (oder V = R 3 und n = 2) ist interessant und Ihnen
vielleicht noch aus der Schule vertraut. Die obige Skizze und die folgenden Argumente gelten
aber ganz allgemein: Der Raum V darf beliebig groß sein, zum Beispiel ein Funktionenraum;
lediglich der Unterraum U sollte zur Vereinfachung endlich-dimensional bleiben, zum Beispiel
der Unterraum der trigonometrischen Polynome vom Grad ≤ k. (Dann wäre dim U = 1 + 2k.)
v ∗ =
n∑
v k e k mit Fourier–Koeffizienten v k = 〈 e k | v 〉.
k=1
Zudem ist v ∗ der einzige Vektor in U, für den v − v ∗ senkrecht steht
auf allen u ∈ U. Dank Pythagoras gilt daher die Bessel–Gleichung:
‖v ∗ ‖ 2 + ‖v − v ∗ ‖ 2
} {{ } } {{ }
Längenquadrat von v ∗
Approximationsfehler
= ‖v‖ 2
}{{}
Längenquadrat von v
Es folgt die Bessel–Ungleichung |v 1 | 2 + · · · + |v n | 2 = ‖v ∗ ‖ 2 ≤ ‖v‖ 2 .
Bestapproximation durch Orthogonalprojektion
Beweis durch Nachrechnen: Wir betrachten den genannten Vektor
v ∗ :=
§R2.3, S.1339
Bestapproximation durch Orthogonalprojektion
Speziell für u = v ∗ gilt somit:
‖v − v ∗ ‖ 2 = ‖v‖ 2 − ‖v ∗ ‖ 2 .
Dieser Abstand ist minimal, denn im Vergleich gilt:
n∑
n∑
n∑
‖v − u‖ 2 − ‖v − v ∗ ‖ 2 = |u k | 2 − u k v k − u k v k +
k=1 k=1 k=1
n∑
n∑
〈 n∑ ∣ ∣∣
n∑ 〉
= (u k − v k )(u k − v k ) =
u k e k u l e l k=1
k=1
k=1 l=1
n∑ n∑
u k u l 〈 e k | e l 〉 Schließlich gilt die behauptete Orthogonalität:
k=1 l=1
〈 n∑ ∣
|u k | 2 = ‖v‖ 2 − 2Re〈 u | v ∗ 〉 + ‖u‖ 2 〈 v − v ∗ ∣∣
n∑ 〉 n∑
n∑
| u 〉 = v − v k e k u k e k = u k v k −
n∑
v k e k mit Koeffizienten v k = 〈 e k | v 〉.
k=1
Für jeden Vektor u ∈ U gilt u = ∑ n
k=1 u ke k mit Koeffizienten u k ∈ K.
Den Abstand zwischen v und u berechnen wir dann wie folgt:
‖v − u‖ 2 = 〈 v − u | v − u 〉 = 〈 v | v 〉 − 〈 v | u 〉 − 〈 u | v 〉 + 〈 u | u 〉
〈
n∑ 〉 〈 n∑ ∣ 〉 ∣∣
= 〈 v | v 〉 − v ∣ u k e k − u k e k v +
= 〈 v | v 〉 −
= 〈 v | v 〉 −
k=1
n∑
u k 〈 v | e k 〉 −
k=1
n∑
u k v k −
k=1
k=1
n∑
u k 〈 e k | v 〉 +
k=1
n∑
u k v k +
k=1
n∑
k=1
n∑
|v k | 2
k=1
|u k − v k | 2 ≥ 0
Gleichheit gilt hierbei nur für u = v ∗ , andernfalls ‖v − u‖ > ‖v − v ∗ ‖.
k=1
l=1
k=1
k=1
§R2.3, S.1340
u k v k = 0