2x2 - IGT

Punktweise Konvergenz
§R1.1, S.1293
Punktweise Konvergenz
§R1.1, S.1294
4
2
0
−2
−4
−2 0 2 4 6 8 10 12 14
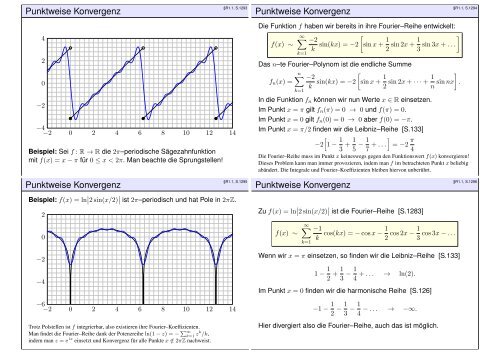
Beispiel: Sei f : R → R die 2π–periodische Sägezahnfunktion
mit f(x) = x − π für 0 ≤ x < 2π. Man beachte die Sprungstellen!
Die Funktion f haben wir bereits in ihre Fourier–Reihe entwickelt:
∞∑
[
−2
f(x) ∼
k sin(kx) = −2 sin x + 1 2 sin 2x + 1 ]
3 sin 3x + . . .
k=1
Das n–te Fourier–Polynom ist die endliche Summe
n∑
[
−2
f n (x) =
k sin(kx) = −2 sin x + 1 2 sin 2x + · · · + 1 ]
n sin nx .
k=1
In die Funktion f n können wir nun Werte x ∈ R einsetzen.
Im Punkt x = π gilt f n (π) = 0 → 0 und f(π) = 0.
Im Punkt x = 0 gilt f n (0) = 0 → 0 aber f(0) = −π.
Im Punkt x = π/2 finden wir die Leibniz–Reihe [S.133]
−2
[1 − 1 3 + 1 5 − 1 ]
7 + . . . = −2 π 4
Die Fourier–Reihe muss im Punkt x keineswegs gegen den Funktionswert f(x) konvergieren!
Dieses Problem kann man immer provozieren, indem man f im betrachteten Punkt x beliebig
abändert. Die Integrale und Fourier–Koeffizienten bleiben hiervon unberührt.
Punktweise Konvergenz
§R1.1, S.1295
Punktweise Konvergenz
§R1.1, S.1296
Beispiel: f(x) = ln ∣ ∣2 sin(x/2) ∣ ∣ ist 2π–periodisch und hat Pole in 2πZ.
2
0
−2
−4
−6
−2 0 2 4 6 8 10 12 14
Trotz Polstellen ist f integrierbar, also existieren ihre Fourier–Koeffizienten.
Man findet die Fourier–Reihe dank der Potenzreihe ln(1 − z) = − ∑ ∞
k=1 zk /k,
indem man z = e ix einsetzt und Konvergenz für alle Punkte x /∈ 2πZ nachweist.
Zu f(x) = ln ∣ ∣2 sin(x/2) ∣ ∣ ist die Fourier–Reihe [S.1283]
f(x) ∼
∞∑
k=1
−1
k cos(kx) = − cos x − 1 2 cos 2x − 1 cos 3x − . . .
3
Wenn wir x = π einsetzen, so finden wir die Leibniz–Reihe [S.133]
1 − 1 2 + 1 3 − 1 4 + . . . → ln(2).
Im Punkt x = 0 finden wir die harmonische Reihe [S.126]
−1 − 1 2 − 1 3 − 1 4 − . . . → −∞.
Hier divergiert also die Fourier–Reihe, auch das ist möglich.