Strategien der Schwingungsanalyse - Kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
1
Strategien der Schwingungsanalyse
(Grundlagen)
1. Prolog – Approximation einer Zeitfunktion
Zur Einführung in das Thema soll die Approximation einer Zeitfunktion x(t) durch
einen Satz von Basisfunktionen ψ i (t) betrachtet werden.
n
x( t)
= a i
ψ ( t)
Gl. 1.1
i = 1
i
Die Approximation soll in einem Intervall der Länge T optimiert werden.
Wählt man ein System von Basisfunktionen, das im Approximationsintervall orthogonal
ist
1
i = k
ψ
i
( t) ψ
k
( t)
= δ
ik
=
Gl. 1.2
0
i ≠ k
T
so erreicht man, dass die einzelnen Terme der Entwicklung bestimmte Eigenschaften
exklusiv in sich vereinigen (im konkreten Fall die Eigenschaft Frequenz)
– das führt zum Begriff der Analyse. Die Einflüsse können getrennt untersucht
und modifiziert werden, die Rücktransformation der Reihe mit modifizierten Termen
simuliert ein geändertes Zeitsignal.
Zur Lösung, d. h. zur Berechnung der Koeffizienten, gibt es verschiedene Ansätze,
z. B. setzt man einfach Identität im Mittel an:
T
n
x(
t)
−ai
ψ
i
( t)
dt
= 0
Gl. 1.3
i = 1
Zur Lösung von Gl. 1.3 ein kurzer Seitenblick auf die lineare Algebra:
Die Lösung eines linearen Gleichungssystem, in Matrixform geschrieben
Ax = y
Gl. 1.4
erhält man für ein reelles System durch Multiplikation mit der Inversen A -1
A
A
−1
−1
Ax = x = A
A = E
−1
y
Gl. 1.5
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
2
In komplexen Systemen tritt an die Stelle der Inversen die adjungierte Matrix A ~
~ ~
AAx = x = Ay
Gl. 1.6
~
AA = E
Der Formalismus wird auf Gl. 1.3 übertragen. Man wählt als Basisfunktionen ein
adjungiertes Funktionenpaar
~ 1
i = k
ψ
i
( t) ψ
k
( t)
= δ
ik
=
Gl. 1.7
0
i ≠ k
T
Multiplikation im Integral vom Gl. 1.3 ergibt
n
~
ψ
k
( t)
x(
t)
−aiψ
i
( t)
dt
= 0
Gl. 1.8
i = 1
T
Aus Gl. 1.7 und Gl. 1.8 erhält man schließlich die gesuchten Koeffizienten
1
ai
= x ~ ψ
i
T
T
( t ) ( t )
dt
Gl. 1.9
Ein geeignetes adjungiertes Funktionensystem für die Frequenzanalyse ist die
Exponentialfunktion
ψ
i
( t)
= e
~ ψ ( t)
= e
ψ
i
( t)
~ ψ
k
( t)
dt = δ
ik
T
i
jω
t
i
jω
t
i
2π
ω
i
= i ⋅ω
1
= i
T
Gl. 1.10
Gl. 1.1 und Gl. 1.9 ergeben mit diesem Ansatz schließlich die Fourriertransformation
(Fourierreihe);
x
a
( t)
i
=
1
=
T
n
i = 1
T
x
a
i
e
( t )
jω
t
e
i
− jω
t
i
dt
Gl. 1.11
Was kann man aus dieser kurzen Ableitung ablesen?
- Die Fouriertransformation ergibt sich als Lösung eines einfachen Approximationsansatzes
- Da alle Basisfunktionen periodisch sind, ist auch die Summe periodisch mit
der Periode 1/T
- Jede periodische Funktion mit der Periode 1/T kann als Summe nach Gl. 1.1
dargestellt werden (Theorem von Fourier)
Es sind dies die üblicherweise sehr abstrakt präsentierten Ansätze zur Fouriertransformation
(ggf. nach dem üblichen Grenzübergang T→∞.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
3
Ausblick
- Ansätze mit anderen Eigenschaften, z. B. die Wavelettransformation, können
durch Einsetzen geeigneter Basisfunktionen auf gleichem Wege abgeleitet
und interpretiert werden
- Die Rolle der Orthogonalität wird sichtbar:
o Konsistenz - bei Erweiterung bleiben die ursprünglichen Koeffizienten
erhalten
o Exklusivität – die Eigenschaften sind vollständig von einem einzigen
Reihenglied beschrieben
- Algorithmen und Eigenschaften für nicht orthogonale Basisfunktionen können
abgeleitet werden.
2. Grundlagen der Fourieranalyse
2.1 Zeitbereich und Frequenzbereich – die Fourierreihe
Ein periodisches Signal mit der Periodizität T kann dargestellt werden als Summe
von harmonischen Komponenten
x(
t)
= x(
t + T )
x(
t)
= a n f
n
cos( 2 π t + Θn
)
Gl. 2.1
1
f =
T
n
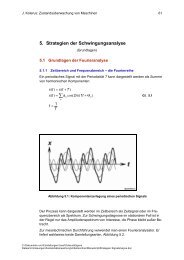
Abbildung 2.1: Komponentenzerlegung eines periodischen Signals
Der Prozess kann dargestellt werden im Zeitbereich als Zeitsignal oder im Frequenzbereich
als Spektrum. Zur Schwingungsdiagnose im stationären Fall ist in
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
4
der Regel nur das Amplitudenspektrum von Interesse, die Phase bleibt außer Betracht.
Zur messtechnischen Durchführung verwendet man einen Fourieranalysator. Er
liefert wahlweise beide Darstellungsarten, Abbildung 2.2.
Abbildung 2.2: Darstellung in Zeitbereich und Frequenzbereich
Man weiß aus Erfahrung: Ereignisse, die im Inneren einer Maschine mit konstanter
Frequenz ablaufen, sind auch von außen akustisch mit gleicher Frequenz
vernehmbar. Da Schall über Gehäuseschwingungen abgestrahlt wird, sind die
Frequenzkomponenten auch im Schwingungsspektrum zu finden. Kennt man Kinematik
und Betriebsdaten, können die Schwingungskomponenten zugeordnet
werden, Abbildung 2.3. Im Zeitsignal sind solche Zuordnungen im Allgemeinen
nicht möglich.
Abbildung 2.3: Identifikation von Schwingungskomponenten
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
5
Es kann jedoch nicht Aufgabe sein, Komponenten lediglich zu identifizieren. Welche
Aufgaben hat man zu erfüllen? Hier zwei Beispiele als Repräsentanten.
2.2 Aufgaben der Frequenzanalyse
2.2.1 Aufgabe A – Schallminderung
.
Abbildung 2.4: Schallminderung
Das Spektrum einer als zu laut beurteilten Maschine wird – zur Berücksichtigung der
Charakteristik des menschlichen Gehörs – mit einer A-Bewertung gewichtet. Im A-
Bewerteten Spektrum kann die schädliche Komponente identifiziert werden. Aus einem
Standard über zulässige Grenzwerte entnimmt man die erforderliche Reduktion.
Die Aufgabe ist von der messtechnischen Seite vollständig gelöst.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
6
2.2.2 Aufgabe B – Lagerdiagnose
Abbildung 2.5: Diagnose eines Wälzlagers
Im Spektrum sind die Laufgeräusche eines Wälzlagers zu identifizieren. Die Qualität
des Lagers kann jedoch aus der Beurteilung eines Einzelspektrums nicht beurteilt
werden.
2.2.3 Warum kann A lösen und B nicht?
Zunächst zu B:
Gemessen werden Schwingungen außen an der Maschine. Interessant als Beurteilungsgrundlage
sind jedoch nicht die Schwingungen außen, sondern die inneren
Kräfte. Diese entziehen sich jedoch einer Messung.
Zwischen Kraft und Schwingung liegt die unbekannte Übertragungsfunktion, die
überdies stark frequenzabhängig ist.
Und nun zu A
A hat prinzipiell das gleiche Problem. Jedoch – die Übertragungsfunktion zwischen
Ursache und Wirkung ist bekannt, ebenso der zulässige Grenzwert. Daher
kann A lösen.
Bleibt B erfolglos?
Nein.
B muss eine andere Strategie entwickeln. Zum Beispiel:
Trendbeobachtung
Die Lagerkomponenten werden über einen längeren Zeitraum beobachtet.
Schwingungen werden immer infolge von Imperfektionen erzeugt, sind also bis
zu einem gewissen Ausmaß normal. Solange sich die Schwingung stabil verhält,
ist das Lager in Ordnung. Erst ein Ansteigen der Komponenten weist auf eine
Verschlechterung hin.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
7
Beurteilung des Laufgeräusches
Erfahrene Beobachter können das Lager auf Grund seines Geräusches beurteilen.
Man kann versuchen, diese subjektive Empfindung signalanalytisch nachzuempfinden.
Es werden dazu verschiedene Analyseverfahren angeboten. Für diese
sei hier ein Begriff geprägt:
Strategische Analysen
Man kennt vielleicht einschlägige Begriffe wie
• Cepstrumanalyse
• Hüllkurvenanalyse
• Hilberttransformation
Die Erläuterung solcher Verfahren läuft sehr schnell in aufwändige mathematische
Ableitungen. Man kann sie verstehen, wenn man entsprechendes Hintergrundwissen
hat oder aufbaut.
Offen bleibt jedoch sehr oft der Aspekt über die allgemeine Anwendbarkeit. Man
hat eine Lösung und sucht das passende Problem.
In diesem Beitrag soll der mathematische Teil im Hintergrund bleiben und durch
grundlegende naturwissenschaftliche Betrachtungen ersetzt werden. Auf diesem
Weg sind Aspekte wesentlich zielführender zu erarbeiten.
3. Strategie
Was ist Strategie?
Man verschafft sich Vorteile.
Man bildet ein unlösbares Problem ab auf ein einfacheres oder leichter zu interpretierbares
Problem.
3.1 Physiologische Strategien
Auf die akustische Beurteilung durch den erfahrenen Beobachter wurde bereits
hingewiesen.
Die menschlichen Sinne haben umfangreiche Strategien zur Erkennung und Beurteilung
geliefert:
• Erkennen von Tönen
• ... von Farben
• ... von Klängen
Die ersten haben mit Frequenzen zu tun.
3.2 Strategien der Physik
Der Physiker (nicht nur er) beobachtet die Natur und versucht sie zu beschreiben.
Die grundsätzlichen Strategien sind
• Experimentelle Physik
• Theoretische Physik
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
8
3.3 Mathematische Strategien
Die Mathematik dient der Beschreibung und Quantifizierung der Beobachtung.
Vordergründig erwartet man vom Mathematiker eine explizite Lösung der Form
x =
Meist kann er sie nicht liefern.
Hat der Mathematiker versagt?
Nein! Voraussetzung wäre, dass das Problem auch explizit darstellbar ist! Meist
ist dies nicht der Fall.
Die Mathematik ist in diesem Zusammenhang als strategisches Instrument zu betrachten.
Es werden, angepasst an z. B. Physik oder Physiologie, Strategien
entwickelt (s. o.). Die grundlegenden seien hier betrachtet.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
9
3.3.1 Zählen
Abbildung 3.1: Zählen
Das Zählen bedarf keiner näheren Erläuterung. Es ist einfach – aber so einfach
doch wieder nicht! Man denke an die lange Entwicklung bis zur Erfindung der
Null, der Basis für systematisches Zählen.
3.3.2 Sortieren (Trennen)
Abbildung 3.2: Sortieren nach Merkmalen
Eine einfache Aufgabe: Wir sortieren Obst in die Kategorien
• Äpfel
• Birnen
• Trauben
• ...
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
10
Abbildung 3.3: Trennung von Sprecher und Sprache
Oder: Wir hören ein gesprochenes Wort. Bei entsprechender Hintergrundkenntnis
können wir trennen nach
• Erkennung des Inhaltes
• Identifizierung des Sprechers
3.3.3 Logarithmieren
Zur Quantifizierung arbeiten unsere Sinne überwiegend auf logarithmischer
Basis.
Mathematisch wird durch Logarithmieren die Multiplikation in die einfachere Addition
transformiert
a * b log a + log b
Gl. 3.1
3.3.4 Integraltransformation
Integraltransformationen transformieren ein analytisches Problem in ein algebraisches
(Differentialrechnung – Algebra).
Am Beispiel Fouriertransformation
jωt
X ( f ) = x(
t)
⋅e
dt
Gl. 3.2
Eine Vereinfachung???
Back to the Roots!
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
11
3.4 Newton und Fourier
Keine Angst!
3.4.1 Isaac Newton
Newton gelang mit Hilfe des Differentialkalküls erstmals die geschlossene Beschreibung
von Bewegungen mit bewegungsabhängigen Kräften. Am Beispiel
des einfachen linearen Schwingers:
m x + kx = F(t)
Gl. 3.3
Wegen der Linearität kann die Kraft F(t) im stationären Fall in eine Fourierreihe
zerlegt werden. Die Einzellösungen für die Fourierterme können superponiert
werden.
mx
+ kx = F cosωt
Zur Vereinfachung des Rechenganges ersetzt man die Winkelfunktion durch die
komplexe Exponentialfunktion. Als schlussendliche Lösung wird nur der Realteil
herangezogen. Hier die Formulierung des Lösungsweges
mx
+ kx = F ⋅e
x = X ⋅e
jωt
jω
t
2
( − mω
+ k) ⋅ X = F
X
F
2
k − mω
= Gl. 3.4
3.4.2 Jean Baptiste Fourier
Eine Allegorie – was sagt Fourier zu Newton?
Die Idee ist zwar genial 1 , aber ich kann aus dieser Beschreibung keine Vorstellung
über den Prozess ableiten – sie entspricht nicht meiner Sinnesempfindung.
Eigentlich trifft das schon in den meisten Fällen für die Beschreibung über ein
´Zeitsignal´ x(t) zu. Ich bin Naturwissenschafter. Ich möchte meine Beobachtung
beschreiben, das ist mein Ziel.
http://www.kolerus.de
1 Albert Einstein sagt später einmal: „Wahrscheinlich der genialste Geistesblitz, den ein
Mensch je hatte.“

J. Kolerus: Strategien der Schwingungsanalyse
12
3.4.2.1 Beschreibung menschlicher Perzeption
Was sind die elementarsten Grundlagen menschlicher Wahrnehmung. Es die Erkennung
von
• Tönen
• Farben
• Akkorden
• Figuren
Man sieht – zumindest drei davon haben mit Frequenzen zu tun.
3.4.2.1.1 Erkennen von Tönen
Wie kann das Erkennen von Tönen mathematisch beschrieben werden?
Man (das neuronale System) prüft, inwieweit ein bestimmter Ton im Signal enthalten
ist.
Die Ähnlichkeit zwischen zwei Signalen x(t) und y(t) wird durch das Kovarianzintegral
beschrieben, Abbildung 3.4.
Cov( x,
y)
= x(
t)
⋅ y(
t)
dt
Gl. 3.5
In Worten: Man multipliziert zeitgleiche Funktionswerte und bildet die Summe.
Abbildung 3.4: Statistisch unabhängige Prozesse
Im Fall statistischer Unabhängigkeit wechselt der Wert des Produktes zwischen
positiv – negativ – groß – klein. Die Summe geht gegen Null.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
13
Der Fall statistischer Abhängigkeit ist in Abbildung 3.5 am Beispiel identischer
Funktionen demonstriert: Das Produkt ist immer positiv, die Summe wird groß.
Abbildung 3.5: Kovarianz identischer Funktionen
Zur Analyse wird ein zu analysierendes Signal x(t) mit einer Testfunktion y(t) verglichen.
Für Zwecke der Tonerkennung wählt man
y( t)
= cosωt
Das Kovarianzintegral nimmt die Form an
Cov( x,
ω)
= x(
t)
cosωtdt
In Abbildung 3.6 bis Abbildung 3.8 sind die Grenzfälle hinsichtlich der Phasenlage
zu sehen. Demnach verfehlt man die Erkennung bei einer Phasenverschiebung
von 90° - das Kovarianzintegral geht gegen Null.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
14
Abbildung 3.6: Tonerkennung – Phasengleichheit
Abbildung 3.7: Tonerkennung – Gegenphasigkeit
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
15
Abbildung 3.8: Tonerkennung – Phasenlage 90°
Das Phasenproblem löst man durch die komplexe Exponentialfunktion als Testfunktion
e
j ω t
= cos ωt
+ j sin ωt
Gl. 3.6
Das Kovarianzintgral wird zum Fourierintegral
jωt
X ( ω)
= x(
t)
e dt
Gl. 3.7
Das Ergebnis, die Spektralfunktion X(ω) wird zwar komplex, das Phasenproblem
ist jedoch beseitigt, Abbildung 3.9.
Handlicher ist oftmals die symbolische Schreibweise
jωt
{ x(
t)}
= X(
ω)
= x(
t)
e dt
Gl. 3.8
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
16
Abbildung 3.9: Zum Fourierintegral
3.4.2.2 Fouriertransformation eines Prozesses
Die Zeitfunktion x(t) beschreibt einen Prozess im Zeitbereich. Gleiches leistet eine
Differentialgleichung. Ist der Prozess linear, kann die Fouriertransformation
Gl. 2.7 auch auf den gesamten Prozess angewendet werden, demonstriert am linearen
Schwinger Gl. 2.3
m x
+ kx = F(t)
Die Fouriertransformation einer abgeleiteten Funktion kann leicht abgeleitet werden
2 {
x(
t)}
= X ( ω)
{
x
( t)}
= jω
X ( ω)
2
{
x
( t)}
= ( jω
) X ( ω)
Man erhält
{
mx
+ kx}
= {
F(
t)}
2
( − mω
+ k)
F(
ω)
X(
ω)
=
2
k − mω
⋅ X ( ω)
= F(
ω)
2 Auf den Beweis der Vertauschbarkeit von Differentiation und Integration für uneigentliche
Integrale soll hier verzichtet werden.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
17
Der Vergleich mit Gl. 2.4 zeigt unmittelbar:
• Der Exponentialansatz für die lineare Differentialgleichung ist
eine Fouriertransformation des Prozesses
• Die Fouriertransformation ist die Beschreibung einfachster
menschlicher Perzeption
3.5 Die Grundrechenarten der Signalanalyse
Auf Basis der in den letzten Abschnitten vorgestellten Strategien sind praktisch
alle Schwingungsanalysen für stationäre Signale aufgebaut. Man wird ihnen im
Folgenden immer wieder begegnen. Sie seien daher hier noch einmal zusammengefasst.
Die drei Grundrechenarten der Signalanalyse
• Sortieren
• Logarithmieren
• Fouriertransformation
4. Die Fouriertransformation
4.1 Definition
Mathematisch akribische Formulierungen sind nicht Gegenstand dieses Beitrages.
Wenn hier einige Formulierungen notiert sind, so dienen sie mehr allgemeinen
Betrachtungen.
Die Fouriertransfomation – Vorwärts und Rückwärtstransformation – in allgemeiner
Schreibweise:
X ( f ) =
{ x(
t)
}
x(
t)
= - 1
=
+∞
−∞
x(
t)
e
+∞
{ X(
f )} =
−∞
− j2πft
X ( f ) e
dt
+ j2πft
df
Gl. 4.1
Es fällt zunächst auf: Als unabhängige Variable im Frequenzbereich wurde die
Frequenz f an Stelle der überwiegend verwendeten Kreisfrequenz ω eingeführt
mit folgenden Vorteilen:
• Die Frequenz liegt der ingenieurmäßigen Betrachtung näher
• Der konstante Faktor vor dem Integral verschwindet
• Die Symmetrie der Fouriertransformation wird sichtbar.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
18
4.2 Eigenschaften
Umkehrbarkeit
Die Fouriertransformation ist eindeutig umkehrbar. Daraus folgt:
Der Informationsgehalt ist in Zeit- und Frequenzbereich gleich.
Linearität
Die Fouriertransformation ist eine lineare Funktion, d. h.
Symmetrie
+
{ x ( t)
+ a x ( t)
} = a {
x ( t)}
a { x ( t)}
a1 1 2 2 1 1
2
2
Bis auf das Vorzeichen im Transformationskern sind Vorwärts- und Rückwärtstransformation
symmetrisch. Da dieses Vorzeichen qualitativ und quantitativ ohne
Bedeutung ist, gilt
Jede Eigenschaft der Transformation gilt gleichermaßen für Vorwärts- und Rückwärtstransformation.
Komplexe Spektren
Setzt man die Eulersche Beziehung Gl. 2.6 in die Transformation Gl. 2.7 ein, so
sieht man unmittelbar die in Tabelle 4.1 zusammengefassten Eigenschaften von
Spektren reeller Zeitsignale
Zeitsignal
Spektrum
beliebig hermitisch 3
reell
gerade
ungerade
Reell, gerade
Imaginär, ungerade
Tabelle 4.1: Spektrale Eigenschaften reeller Zeitsignale
Die Spektren der wichtigsten Elementarfunktionen sind in Abbildung 4.1 zu
sehen.
3 Die hermitische Eigenschaft heißt gerader Realteil und ungerader Imaginärteil
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
19
Zeitbereich
Frequenzbereich
f
f
Abbildung 4.1: Spektren harmonischer Zeitsignale
4.3 Fast Fourier Transformation (FFT)
Zur praktischen Durchführung wir aus dem Zeitsignal ein Abschnitt der Länge T
ausgeschnitten und nach beiden Seiten periodisch fortgesetzt. Die Fourierreihe
dieses periodischen Ersatzsignals wird als Repräsentant des Spektrums gebildet.
Daraus ergeben sich Einschränkungen bzw. Grenzen.
Abbildung 4.2: Ersatzsignal zur Berechnung des Spektrums
Unschärfe
Das so berechnete Spektrum ist ein Linienspektrum, Abbildung 4.3, mit der Frequenzauflösung
1/T. Dieser Zusammenhang zwischen Blocklänge T und Bandbreite
B ist Ausdruck der Unschärferelation der Frequenzanalyse
B = 1
Gl. 4.2
T
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
20
Abbildung 4.3: Linienspektrum
Leakage
Die periodische Fortsetzung erzeugt Sprungstellen an der Nahtstelle, die zu Nebenlinien
im Spektrum führen, Abbildung 4.4. Man nennt diesen Effekt Leakage,
da sozusagen die Signalenergie zerfließt. Durch Hanningbewertung – Multiplikation
des Zeitsignals mit einem cos²-Fenster – werden die Nahtstellen beseitigt.
Abbildung 4.4: Leakage durch Nahtstellen – Hanningbewertung
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
21
Diskrete Fouriertransformation
Abbildung 4.5 zeigt den Weg vom Fourierintegral zur Diskreten Fouriertransformation
(DFT). Ausgehend vom kontinuierlichen und unendlichen Fourerintegral,
obere Reihe 4 , wird durch Fensterung wie beschrieben, ein diskretes Spektrum
gebildet, Reihe 2.
Zur Berechnung werden aus dem kontinuierlichen Spektrum äquidistante Stützstellen
des Zeitsignals herangezogen. Aus Symmetriebetrachtungen ergibt sich:
Die Diskretisierung des Zeitsignals führt zu einem periodischen Spektrum, Reihe
3.
In Reihe 4, der letzten Reihe von Abbildung 4.5, sieht man schließlich das Endergebnis,
das diskrete Spektrum des gefensterten, diskretisierten Zeitsignals.
Man erhält ein periodisches Linienspektrum. Aus Symmetriegründen enthält –
wegen der Symmetrie des Amplitudenspektrums – der im Bild indizierte Teil des
Spektrums die gesamte Information. Er wird im Analysator angezeigt.
Aliasing
Wegen der Periodizität des Spektrums werden Frequenzkomponenten im periodischen
Spektrum gespiegelt, sie treten mehrfach auf. Aus diesem Grund muss
Sorge getragen werden, dass im analysierten Signal keine hochfrequenten Komponenten
oberhalb der halben Abtastfrequenz enthalten sind (Antialiasingfilter).
Solche Komponenten würden die Eindeutigkeit stören.
http://www.kolerus.de
4 Im Bild wurde wegen der besseren Darstellbarkeit ein gerades Zeitsignal mit reellem
Spektrum als Beispiel herangezogen

J. Kolerus: Strategien der Schwingungsanalyse
22
Zeitbereich
Frequenzbereich
x(t)
X(f)
kontinuierlich
t
kontinuierlich
f
x(t)
X(f)
∆f = 1_ T
periodisch
T
x(t)
∆t
t
diskret
(Linienspektrum)
X(f)
Aliasing
f
diskret
(gesampelt)
t
periodisch
x(t)
∆t
X(f)
∆f = 1_ T
diskret (periodisch)
t
Linienspektrum (periodisch)
f
T
F = __ 1
∆t
Abbildung 4.5: Die diskrete Fouriertransformation (DFT)
.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
23
5. Strategische Analysen
Die Frequenzanalyse bildet zunächst eine Basis für die Fehlerdiagnose. Aufbauend
auf diesem Konzept sind Strategien zur weiteren Interpretation einzusetzen.
Genannt wurde schon die Trendbeobachtung. In diesem Abschnitt werden aufbauende
Analysen vorgestellt.
Der erfahrene Beobachter hört mechanische Fehler oft am Klang einer Maschine.
Was heißt Klang? Das Laufgeräusch klingt einfach verändert. Unregelmäßigkeiten
wie Eiern oder Klicken. Effekte dieser Art zeigen sich als regelmäßige
Strukturen im Spektrum. Verstärktes Auftreten von Harmonischen bei Klangveränderung.
Modulationen im anderen Fall. Ziel der strategischen Analysen soll
das Aufspüren solcher Strukturen sein. Dabei wird die Interpretation nach Gesichtspunkten
menschlicher Wahrnehmung wieder im Vordergrund stehen.
5.1 Cepstrumanalyse
Der Begriff Cepstrum ist gebildet aus der Umdrehung des Wortes Spektrum, assoziiert
vom dahinterliegenden Algorithmus. Man führt letztendlich eine Fourier-
Rückwärtstransformation vom Frequenzbereich in den Zeitbereich aus. Zur verbalen
Unterscheidung vom ursprünglichen Zeitbereich hat man eine entsprechende
Nomenklatur eingeführt. So wird z. B. die unabhängige Variable mit der
Dimension Zeit hier Quefrenz genannt.
5.1.1 Harmonische – das Leistungscepstrum
Abbildung 5.1: Spektrum einer Motor/Lüfter Kombination (linearer Amplitudenmaßstab)
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
24
Abbildung 5.2: Harmonische in Spektrum und Cepstrum
Abbildung 5.1 zeigt ein Spektrum gemessen an einer Motor/Lüfter Kombination.
Zu sehen ist im wesentlichen eine einzige Drehzahlkomponente.
In Abbildung 5.2 – zunächst wird nur das große Teilbild betrachtet – ist im logarithmischem
Amplitudenmaßstab eine Familie von Harmonischen (mit Cursoren
indiziert) ist deutlich zu erkennen.
Ein Zeitsignal mit solchen regelmäßigen Strukturen im Zeitbereich – also Periodizitäten
– würde im Spektrum Linien bei den entsprechenden Frequenzen zeigen.
Entsprechendes ist in Anwendung des Symmetrieprinzips nach der Fourier-
Rücktransformation im Cepstrum zu erwarten (kleines Teilbild). Die im Cepstrum
entsprechend den Harmonischen indizierte Linie ist der erste Repräsentant des
´Klanges´.
Als Gedankenexperiment wird das gleiche Spektrum betrachtet, aus dem die
Grundfrequenz – hier künstlich – entfernt wurde, Abbildung 5.3.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
25
Abbildung 5.3: ... fehlende Grundfrequenz
Obwohl die Grundfrequenz fehlt, ist die Harmonischenfamilie im Cepstrum nach
wie vor scharf indiziert. Aus dem Spektrum allein wäre das Auffinden jetzt schon
problematisch.
Die erste Eigenschaft des Cepstrums ist als die Möglichkeit, die fehlende Grundfrequenz
aus dem Spektrum zu rekonstruieren. Dies Fähigkeit hat auch das
menschliche Gehör: So kann man z. B. auch am klassischen analogen Telefon
unterscheiden, ob man mit einem Mann oder einer Frau spricht – was vom Frequenzgang
her eigentlich nicht möglich sein sollte.
Da das hier eingeführte Cepstrum aus der Fourier-Rücktransformation des Leistungsspektrums
(ohne Phaseninformation) abgeleitet wird, bezeichnet man es
als Leistungscepstrum. Abbildung 5.4 zeigt noch einmal schematisch die Definition.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
26
Zeitbereich
Frequenzbereich
C ( τ )
P
log(F (f))
xx
∆f
1__ __ 2
∆f ∆f
Leistungscepstrum
τ
f
0
Leistungsspektrum
mit regelmäßiger Struktur
f
Abbildung 5.4: Das Leistungscepstrum – Definition
Abbildung 5.5: Spektren und Cepstren an 2 Messpunkten
Einen interessanten Aspekt zeigt Abbildung 5.5: An einer Maschine wurden
Spektren und Cepstren simultan an zwei Messpunkten erfasst – sie repräsentieren
also den selben Betriebszustand.
Man sieht: Die Spektren weisen zwar eine gewisse Verwandtschaft, aber doch
deutliche Unterschiede auf. Die Linien in den Cepstren – typisch für Zahnradgetriebe
– sind für beide Messpunkte praktisch identisch. Die Verwandtschaft
kommt im Cepstrum weit besser zum Ausdruck.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
27
5.1.2 Entfaltung – das komplexe Cepstrum
Für den allgemeinen Fall des komplexen Cepstrums sind die Verhältnisse im
Flussdiagramm Abbildung 5.6 veranschaulicht.
Abbildung 5.6: Berechnung des Cepstrums
Im ursprünglichen Zeitbereich sind Kraft und Schnelle, mathematisch gesehen,
über die sogenannte Faltung verknüpft, Abbildung 5.7. Denkt man sich das Eingangssignal
(Kraft) als Folge von Einzelimpulsen zu den Zeitpunkten t 1 , t 2 , t 3 ... so
kann man die Reaktion (Schwingung) als Folge von entsprechend zeitverschobenen
Impulsantworten konstruieren. Demnach ist die Schwingung zu jedem
Zeitpunkt beeinflusst durch (theoretisch) alle vergangenen Einzelimpulse.
Faltungssatz
Aus der Faltung im Zeitbereich wird durch die Fouriertransformation eine Multiplikation
im Frequenzbereich.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
28
Abbildung 5.7: Die Faltung von Kraft und Impulsantwort
t
−∞
y( t)
= x(
t)
∗h(
t)
= x(
τ ) ⋅ h(
t −τ
) dτ
Gl. 5.1
Y( f ) = y( t) e − j 2π
ft −
dt e j 2π
= ft x( τ ) ⋅ h( t − τ ) dτ
dt
− j 2πfτ
− j 2πfu
Y( f ) = e x( τ ) dτ
e h( u)
du
{ x( t) ∗ h( t) } = { x( t) }. { h( t)
}
{ x( t) ⋅ h( t) } = { x( t) } ∗
{ h( t)
}
Gl. 5.2
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
29
Daraus resultiert auch eine mathematische Erklärung der besseren Trennbarkeit
im Frequenzbereich.
Man rufe sich jetzt das Strategische Konzept in Erinnerung, die Grundrechenarten
der Signalanalyse (Abschnitt 3.5)!
• Die Fouriertransformation wurde schon durchgeführt.
• Durch Logarithmieren wird die Multiplikation zur Addition
• Die Addition bleibt bei der Fourier-Rückwärtstransformation wegen
der Linearität erhalten. Das Cepstrum C y des Ausganges wird getrennt
in die Cepstren C x von Kraft und C h von Impulsantwort.
Das Schema beschreibt exakt die Möglichkeit der Trennung von Sprecher und
Sprache, Abbildung 3.3.
Auf dieser Basis lässt sich auch die Ähnlichkeit der Cepstren in Abbildung 5.5 interpretieren:
Die Linien sind der kraftbasierte Anteil, die Kraft ist für beide Messpunkte
die gleiche. Die Übertragungsfunktionen – repräsentiert durch die
Cepstren im Bereich niedriger Quefrenzen – sind durchaus unterschiedlich.
Können wir auf diesem Weg die Erregerkraft messen?
Der Gedanke ist reizvoll, wäre die Kraft doch unsere eigentliche Zielgröße. Die
Messung scheitert jedoch an der Kalibrierbarkeit. Wieder die perzeptive Entsprechung:
Aus der Lautstärke kann nicht unterschieden werden zwischen einem
lauten Geräusch hinter einer dicken Wand oder einem leisen
hinter einer dünnen.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
30
5.2 Hüllkurvenanalyse
Bei vielen Geräuschen steckt die Information in einer Hüllkurve. Läuft ein Getriebe
gleichmäßig, empfindet man das (laute) Geräusch normal. Ein Eiern oder
Knacken wird als unnormal interpretiert – man sagt, es eiert, knackt. Man hat
damit das Knacken vom Gesamtgeräusch getrennt – man hat demoduliert. Wieder
die Aufgabe der Trennung ...
5.2.1 Modulation
Abbildung 5.8: Amplitudenmodulation
Abbildung 5.8 zeigt als einfachsten Repräsentanten eine amplitudenmodulierte
Sinusfunktion, also Sinus (Träger) mit zeitveränderlicher Amplitude (Modulation).
Im Zeitbereich mathematisch zu beschreiben durch eine Multiplikation:
A
m
x( t) = 1
+ cosωmt ⋅ AT cosωT
t =
A
T
= A cosω t + A cosω t ⋅ cosω
t =
T T m m T
Am
Am
= AT
cosωTt
+ cos ( ωT
+ ωm
) t + cos ( ωT
− ωm)
t
2 2
Gl. 5.3
Die kurze mathematische Beschreibung Gl. 4.3 liefert zusammen mit dem Bild alle
grundlegenden Informationen:
• Im Zeitbereich sind Träger und Modulation durch Multiplikation verknüpft
• Im Frequenzbereich wird das Spektrum der Modulation mit seinem
Ursprung and die Stelle der Trägerfrequenz verschoben
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
31
• Die Multiplikation im Zeitbereich wird zur Faltung im Frequenzbereiches
(Symmetrie – Faltungssatz, Abschnitt 5.1.2)
Im allgemeinen Fall wird die Modulation eine periodische Funktion mit mehren
Harmonischen sein, entsprechend wird im Spektrum um die Trägerfrequenz f T
eine Familie von Linien im Abstand von Vielfachen der Modulationsfrequenz –
eine Seitenbandfamilie auftreten.
Zwei Aufgaben sind – gespiegelt am Muster des schadhaften Zahnradgetriebes –
zu sehen,
• Auffinden der Seitenbandfamilie
• Extraktion der Modulation = Demodulation
5.2.2 Detektion von Seitenbändern
Die Detektion von Seitenbändern erfolgt mit der Cepstrumanalyse wie schon beschrieben.
5.2.3 Der Ansatz von Hilbert
Hilberts Gedanke hat eigentlich einen ganz anderen Ansatzpunkt: Ein lineares
System ist charakterisiert durch seine Impulsantwort im Zeitbereich. Die Fouriertransformation
der Impulsantwort ist die komplexe Übertragungsfunktion im
Frequenzbereich.
Im Unterschied zum Signal ist die Impulsantwort auf Grund des Kausalitätsprinzips
immer einseitig. Hilbert hat die Konsequenzen für die Übertragungsfunktion
untersucht und formuliert: Realteil und Imaginärteil hängen über die Hilberttransformation
zusammen.
5.2.4 Demodulation - Hiberttransformation
Symmetriebetrachtung des Hilbertschen Ansatzes:
• Die Fouriertransformation liefert positive und negative Frequenzen
• Das Spektrum reeller Zeitsignale ist hermitisch
• Wir hören nur Frequenzen
• Perzeptiv sind negative Frequenzen nicht zu interpretieren
• Wie sieht ein Zeitsignal mit einseitigem Spektrum aus?
Zunächst: Das gesuchte Zeitsignal ist komplex. Man nennt es das Analytische
Zeitsignal.
Ableitung und Zusammenhänge kann man an Hand von Abbildung 5.9 nachvollziehen.
Im linken Teilbild ist – gezeigt an einer Einzelkomponente – das zweiseitige komplexe
Spektrum mit der hermitischen Eigenschaft zu sehen. Das rechte Spektrum
zeigt das Spektrum entsprechend dem Höreindruck: Die gesamte Energie auf einer
Komponente, der mit positiver Frequenz. Dazwischen der spektrale Anteil der
zum gewünschten Ergebnis führt.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
32
Abbildung 5.9: Analytisches Zeitsignal – Hilberttransformation
Die Prozedur lässt sich aus der Bildfolge ablesen.
Schreibt man für das analytische Zeitsignal
so sieht man
xˆ
( t)
= x(
t)
+ j ⋅ x
~
( t)
• Der Realteil des analytischen Zeitsignals ist gleich dem klassischen
reellen Zeitsignal x(t)
• Das Spektrum des Imaginärteils x
~
( t ) entsteht daraus durch Drehung
des Realteils um –90° und des Imaginärteils um + 90°
Abbildung 5.10: Zur Bildung der Hilberttransformation
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
33
Der Zusammenhang zwischen Realteil und Imaginärteil des Zeitsignals wird
Hiberttransformation genannt. Ihre explizite (komplizierte) mathematische Formulierung
kann an dieser Stelle unterbleiben. Sie nach dem Schema von
Abbildung 5.10 nur mit den Grundrechenarten der Signalanalyse zu ermitteln.
Beispiel: Hilberttransformation des Cosinus
Aus Abbildung 4.1 und Abbildung 5.10 kann man direkt ablesen
• Die Hilberttransformierte von cosωt ist sinωt
• Das analytische Zeitsignal ist die Exponentialfunktion
x(
t)
= Acosω
t
x
~
( t)
= Asin
ω t
xˆ(
t)
= Ae
jω
t
Gl. 5.4
Man erinnert sich an Newton (Abschnitt 3.4.1): Die Einführung der Exponentialfunktion
als Notierung, ursprünglich argumentiert als eine Art Bequemlichkeit,
war bereits die Hilberttransformation. Neu wird lediglich die Interpretation des
Imaginärteiles.
Der Betrag des analytischen Zeitsignals Gl. 4.4 ist die Amplitude A, die Hüllkurve.
Beispiel: Amplitudenmodulation
x(
t)
= A(
t)cosω
t
x
~
( t)
= A(
t)sin
ω t
xˆ(
t)
= A(
t)
e
jω
t
Gl. 5.5
Die Relation Gl. 4.5 ist gültig, so lange der Frequenzbereich der zeitabhängigen
Amplitude A(t) unterhalb der Trägerfrequenz liegt.
Die Hilberttransformation ist ein Mittel zur Demodulation. Die Ausführung erfolgt
mit den Grundrechenarten der Signalanalyse.
http://www.kolerus.de

J. Kolerus: Strategien der Schwingungsanalyse
34
6. Zusammenfassung
Sortieren
Cepstrum
Demodulation
Kraft Impedanz Schwingung Schwingung
Signal Struktur Signal Signal
Sprache Sprecher Äpfel Birnen
Tabelle 6.1: Eigenschaften strategischer Analysen
7. Schrifttum
Papoulis, A.: Signal Analysis.McGraw-Hill 1977
Bendat, J.S.: The Hilbert Transform and Applications to Correlation Measurements.
Bruel&Kjaer Application Note BT 0008-11
Randall, R. B.: Frequency Analysis. Bruel&Kjaer 1987
Kolerus, J.: Zustandsüberwachung von Maschinen. 3. Auflage,
Expert Verlag 2000
http://www.kolerus.de
http://www.kolerus.de