booklet format - inaf iasf bologna

Temporal Data Analysis A.A. 2011/2012
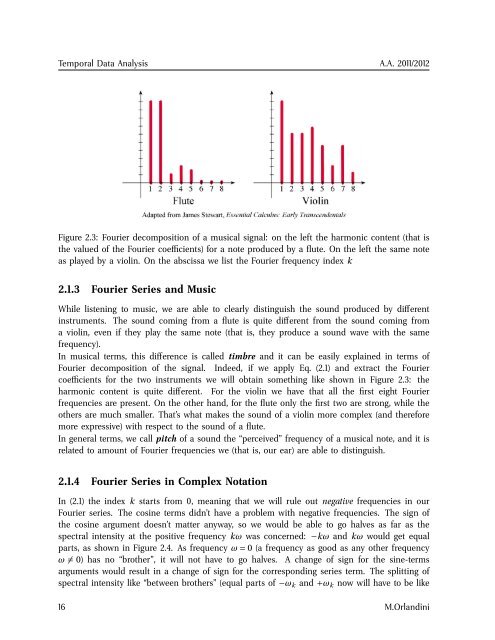
Figure 2.3: Fourier decomposition of a musical signal: on the left the harmonic content (that is
the valued of the Fourier coefficients) for a note produced by a flute. On the left the same note
as played by a violin. On the abscissa we list the Fourier frequency index k
2.1.3 Fourier Series and Music
While listening to music, we are able to clearly distinguish the sound produced by different
instruments. The sound coming from a flute is quite different from the sound coming from
a violin, even if they play the same note (that is, they produce a sound wave with the same
frequency).
In musical terms, this difference is called timbre and it can be easily explained in terms of
Fourier decomposition of the signal. Indeed, if we apply Eq. (2.1) and extract the Fourier
coefficients for the two instruments we will obtain something like shown in Figure 2.3: the
harmonic content is quite different. For the violin we have that all the first eight Fourier
frequencies are present. On the other hand, for the flute only the first two are strong, while the
others are much smaller. That’s what makes the sound of a violin more complex (and therefore
more expressive) with respect to the sound of a flute.
In general terms, we call pitch of a sound the “perceived” frequency of a musical note, and it is
related to amount of Fourier frequencies we (that is, our ear) are able to distinguish.
2.1.4 Fourier Series in Complex Notation
In (2.1) the index k starts from 0, meaning that we will rule out negative frequencies in our
Fourier series. The cosine terms didn’t have a problem with negative frequencies. The sign of
the cosine argument doesn’t matter anyway, so we would be able to go halves as far as the
spectral intensity at the positive frequency kω was concerned: −kω and kω would get equal
parts, as shown in Figure 2.4. As frequency ω = 0 (a frequency as good as any other frequency
ω ≠ 0) has no “brother”, it will not have to go halves. A change of sign for the sine-terms
arguments would result in a change of sign for the corresponding series term. The splitting of
spectral intensity like “between brothers” (equal parts of −ω k and +ω k now will have to be like
16 M.Orlandini