Chapter 9: Introduction to Hypothesis Testing

More documents

Recommendations

Info

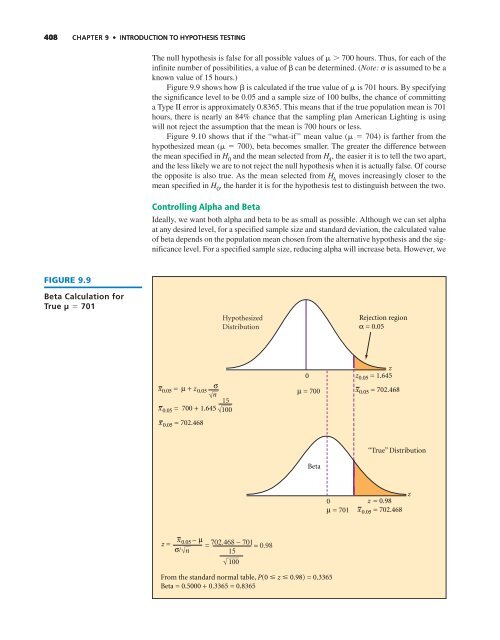
408 CHAPTER 9 • INTRODUCTION TO HYPOTHESIS TESTING The null hypothesis is false for all possible values of 700 hours. Thus, for each of the infinite number of possibilities, a value of can be determined. (Note: is assumed to be a known value of 15 hours.) Figure 9.9 shows how is calculated if the true value of is 701 hours. By specifying the significance level to be 0.05 and a sample size of 100 bulbs, the chance of committing a Type II error is approximately 0.8365. This means that if the true population mean is 701 hours, there is nearly an 84% chance that the sampling plan American Lighting is using will not reject the assumption that the mean is 700 hours or less. Figure 9.10 shows that if the “what-if” mean value ( 704) is farther from the hypothesized mean ( 700), beta becomes smaller. The greater the difference between the mean specified in H 0 and the mean selected from H A , the easier it is to tell the two apart, and the less likely we are to not reject the null hypothesis when it is actually false. Of course the opposite is also true. As the mean selected from H A moves increasingly closer to the mean specified in H 0 , the harder it is for the hypothesis test to distinguish between the two. Controlling Alpha and Beta Ideally, we want both alpha and beta to be as small as possible. Although we can set alpha at any desired level, for a specified sample size and standard deviation, the calculated value of beta depends on the population mean chosen from the alternative hypothesis and the significance level. For a specified sample size, reducing alpha will increase beta. However, we FIGURE 9.9 Beta Calculation for True µ 701 Hypothesized Distribution Rejection region α = 0.05 x 0.05 = μ + z 0.05 σ n x 0.05 = 700 + 1.645 x 0.05 = 702.468 15 100 0 μ = 700 z z 0.05 = 1.645 x 0.05 = 702.468 Beta “True” Distribution 0 μ = 701 z = 0.98 x 0.05 = 702.468 z z = x 0.05 – μ = 702.468 − 701 = 0.98 σ/ n 15 100 From the standard normal table, P(0 z 0.98) = 0.3365 Beta = 0.5000 + 0.3365 = 0.8365
CHAPTER 9 • INTRODUCTION TO HYPOTHESIS TESTING 409 FIGURE 9.10 Beta Calculation for True 704 Hypothesized Distribution Rejection region α = 0.05 0 μ = 700 z z 0.05 = 1.645 x 0.05 = 702.468 (see Figure 9.10) Beta “True” Distribution z = x 0.05 – μ = 702.468 704 = 1.02 σ/ n 15 100 z = 1.02 x 0.05 = 702.468 0 μ = 704 From the standard normal table P(–1.02 z 0) = 0.3461 Beta = 0.5000 0.3461 = 0.1539 z can simultaneously control the size of both alpha and beta if we are willing to increase the sample size. The American Lighting Company planned to take a sample of 100 light bulbs. In Figure 9.9, we showed that beta 0.8365 when the “true” population mean was 701 hours. This is a very large probability and would be unacceptable to the company. However, if the company is willing to incur the cost associated with a sample size of 500 bulbs, the probability of a Type II error could be reduced to 0.5596, as shown in Figure 9.11. This is a big improvement and is due to the fact that the standard error (/ n ) is reduced because of the increased sample size. SUMMARY Calculating Beta The probability of committing a Type II error can be calculated using the following steps. 1. Formulate the null and alternative hypotheses. 2. Specify the significance level. (Hint: Draw a picture of the hypothesized sampling distribution showing the rejection region(s) and the acceptance region found by specifying the significance level.) 3. Determine the critical value, z , from the standard normal distribution. 4. Determine the critical value, x z/ n for an upper-tail test, or x z/ n for a lower-tail test. 5. Specify the stipulated value for μ, the “true” population mean for which you wish to compute β. (Hint: Draw the “true” distribution immediately below the hypothesized distribution.) 6. Compute the z-value based on the stipulated population mean as x z n 7. Use the standard normal table to find β, the probability associated with “accepting” the null hypothesis when it is false.
Page 1 and 2: Chapter NINE Introduction to Hypoth
Page 3 and 4: CHAPTER 9 • INTRODUCTION TO HYPOT
Page 33: CHAPTER 9 • INTRODUCTION TO HYPOT

Chapter 9: Introduction to Hypothesis Testing

Create successful ePaper yourself

Delete template?

Save as template?