Undrained Load Capacity of Torpedo Anchors in ... - laceo - UFRJ

where:
σ y
k VM = (13)
3
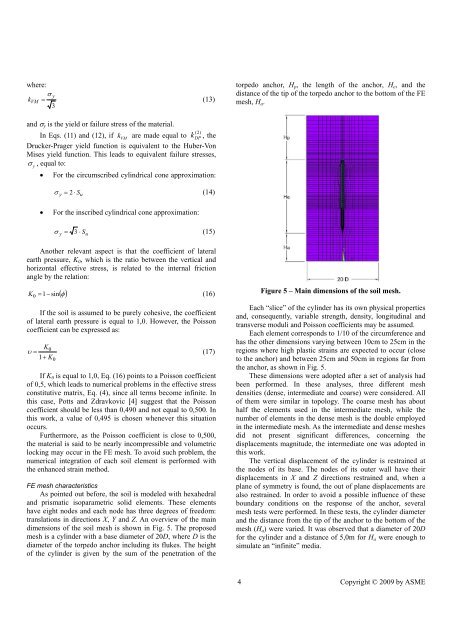
torpedo anchor, H p , the length of the anchor, H e , and the
distance of the tip of the torpedo anchor to the bottom of the FE
mesh, H a .
and σ y is the yield or failure stress of the material.
(2)
In Eqs. (11) and (12), if k VM
are made equal to k
DP , the
Drucker-Prager yield function is equivalent to the Huber-Von
Mises yield function. This leads to equivalent failure stresses,
σ
y
, equal to:
• For the circumscribed cylindrical cone approximation:
σ y = 2 ⋅ S u
(14)
• For the inscribed cylindrical cone approximation:
σ y = 3 ⋅ S u
(15)
Another relevant aspect is that the coefficient of lateral
earth pressure, K 0 , which is the ratio between the vertical and
horizontal effective stress, is related to the internal friction
angle by the relation:
( )
K 0 = 1−
sin φ
(16)
If the soil is assumed to be purely cohesive, the coefficient
of lateral earth pressure is equal to 1,0. However, the Poisson
coefficient can be expressed as:
K0
υ =
(17)
1+
K
0
If K 0 is equal to 1,0, Eq. (16) points to a Poisson coefficient
of 0,5, which leads to numerical problems in the effective stress
constitutive matrix, Eq. (4), since all terms become infinite. In
this case, Potts and Zdravkovic [4] suggest that the Poisson
coefficient should be less than 0,490 and not equal to 0,500. In
this work, a value of 0,495 is chosen whenever this situation
occurs.
Furthermore, as the Poisson coefficient is close to 0,500,
the material is said to be nearly incompressible and volumetric
locking may occur in the FE mesh. To avoid such problem, the
numerical integration of each soil element is performed with
the enhanced strain method.
FE mesh characteristics
As pointed out before, the soil is modeled with hexahedral
and prismatic isoparametric solid elements. These elements
have eight nodes and each node has three degrees of freedom:
translations in directions X, Y and Z. An overview of the main
dimensions of the soil mesh is shown in Fig. 5. The proposed
mesh is a cylinder with a base diameter of 20D, where D is the
diameter of the torpedo anchor including its flukes. The height
of the cylinder is given by the sum of the penetration of the
Figure 5 – Main dimensions of the soil mesh.
Each “slice” of the cylinder has its own physical properties
and, consequently, variable strength, density, longitudinal and
transverse moduli and Poisson coefficients may be assumed.
Each element corresponds to 1/10 of the circumference and
has the other dimensions varying between 10cm to 25cm in the
regions where high plastic strains are expected to occur (close
to the anchor) and between 25cm and 50cm in regions far from
the anchor, as shown in Fig. 5.
These dimensions were adopted after a set of analysis had
been performed. In these analyses, three different mesh
densities (dense, intermediate and coarse) were considered. All
of them were similar in topology. The coarse mesh has about
half the elements used in the intermediate mesh, while the
number of elements in the dense mesh is the double employed
in the intermediate mesh. As the intermediate and dense meshes
did not present significant differences, concerning the
displacements magnitude, the intermediate one was adopted in
this work.
The vertical displacement of the cylinder is restrained at
the nodes of its base. The nodes of its outer wall have their
displacements in X and Z directions restrained and, when a
plane of symmetry is found, the out of plane displacements are
also restrained. In order to avoid a possible influence of these
boundary conditions on the response of the anchor, several
mesh tests were performed. In these tests, the cylinder diameter
and the distance from the tip of the anchor to the bottom of the
mesh (H a ) were varied. It was observed that a diameter of 20D
for the cylinder and a distance of 5,0m for H a were enough to
simulate an “infinite” media.
4 Copyright © 2009 by ASME