Bound for Success Scope and Sequence Statements

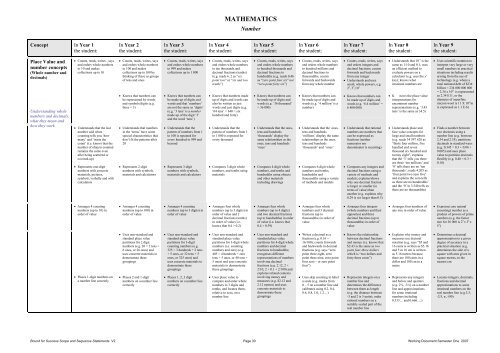
MATHEMATICSNumberConcept In Year 1the student:In Year 2the student:In Year 3the student:In Year 4the student:In Year 5the student:In Year 6the student:In Year 7the student:In Year 8the student:In Year 9the student:Place Value andnumber concepts(Whole number anddecimals)Understanding wholenumbers and decimals;what they mean andhow they work• Counts, reads, writes , saysand orders whole numbersto 10 and makescollections up to 10• Understands that the lastnumber said whencounting tells you ‘howmany’ and ‘trusts thecount’ (i.e. knows that thenumber of objects countedremains the same evenafter being scattered orcovered-up)• Represents one-digitnumbers with concretematerials, pictures,symbols, verbally and withcalculators• Counts, reads, writes, saysand orders whole numbersto 100 and makescollections up to 100 bythinking of these as groupsof tens and ones• Knows that numbers canbe represented by wordsand symbols/digits (e.g.three = 3)• Understands that numbersin the ‘teens’ have somespecial characteristics thatdon’t fit the patterns after20• Represents 2-digitnumbers with symbols,materials and calculators• Counts, reads, writes, saysand orders whole numbersto 999 and makescollections up to 1 000• Knows that numbers canbe made up of digits andwords and that ‘numbers’are not the same as ‘digits’(e.g. ‘3 tens’ is a numbermade up of the digit ‘3’and the word ‘tens’)• Understands that thepattern of numbers from 1to 100 is repeated forevery hundred to 999 andbeyond• Represents 3-digitnumbers with symbols,materials and calculators• Counts, reads, writes, saysand orders whole numbersto ten thousands anddecimal fractions (tenths)(e.g. reads 6..2 as “sixpoint two” or “six and twotenths”)• Knows that numbers madeup of digits and words canalso be written as justwords and just digits (e.g.’64 tens’ = 640 = sixhundred and forty)• Understands that thepattern of numbers from 1to 1 000 is repeated forevery thousand• Compares 3-digit wholenumbers, and tenths usingmaterials• Counts, reads, writes, saysand orders whole numbersto hundred thousands anddecimal fractions tohundredths (e.g. reads 0.46as “zero point four six” not“zero point forty six”)• Knows that numbers canbe made up of digits andwords (e.g. ’36 thousand’= 36 000)• Understands that the ones,tens and hundreds‘thousands’ display thesame relationships as theones, tens and hundreds‘ones’• Compares 4-digit wholenumbers, and tenths andhundredths using objectsand other materialsincluding drawings• Counts, reads, writes, saysand orders whole numbersto hundred millions anddecimal fractions tothousandths; countsforwards and backwardsfrom any whole number• Knows that numbers canbe made up of digits andwords (e.g. ‘4 million’ is anumber)• Understands that the ones,tens and hundreds‘millions’ display the samerelationships as the ones,tens and hundreds‘thousands’ and ‘ones’• Compares 6-digit wholenumbers and tenths,hundredths andthousandths using a varietyof methods and models• Counts, reads, writes, saysand orders integers anddecimal fractions; countsforwards and backwardsfrom any integer• Understands and usessmall, whole powers, e.g.2 3 , 3 5 ,10 3• Knows that numbers canbe made up of digits andwords (e.g. ‘6.4 million’ =6 400 000)• Understands that rationalnumbers are numbers thatcan be expressed asfractions (neithernumerator nordenominator is recurring)• Compares any integers anddecimal fractions using avariety of methods andmodels; explains/showswhy one decimal fractionis larger or smaller (interms of value) thananother (e.g. explains why0.29 is not larger than 0.3)• Understands that 10 -1 is thesame as 1/10 and 0.1; usesan efficient method toevaluate powers on acalculator (e.g. uses the x ykey); knows whatirrational numbers are• K nows the place valueinterpretations foruncommon numberrepresentations (e.g. ‘3.45tens’ is the same as 34.5)• Understands place andface value concepts forlarge and small numbers(e.g. reads 34 597 628 as“thirty four million, fivehundred and seventhousand six hundred andtwenty eight”, explainsthat the ‘3’ tells you thereare three ‘ten millions’ and‘0’ tells there are no ‘tenthousands’; reads 4.205 as‘four point two zero five’and explains the zero tellsus there are no hundredths’and the ‘0’ in 3.540 tells usthere are no thousandths)• Uses scientific notation tointerpret very large or verysmall numbers in practicalsituations including resultsarising from the use oftechnology (e.g. where atotal national debt of $234billion = 234 000 000 000= 2.34 x 10 11 is representedas 2.34 E11, or thediameter of superfinemicron wool is 11 X 10 -6 mis expressed as 1.1 E-6)• Finds a number betweentwo decimals using anumber line (e.g. between2.34 and 2.35), partitionsdecimals in standard ways(e.g. 0.345 = 0.3 + 0.04 +0.005) and uses placevalue to partition decimalsflexibly (e.g. 0.48 = 0.3 +0.18)• Arranges 4 countingnumbers (up to 10) inorder of value• Arranges 4 countingnumbers (up to 100) inorder of value• Arranges 4 countingnumbers (up to 3 digits) inorder of value• Arranges four wholenumbers (up to 3 digits) inorder of value and 2decimal fractions (tenths)in order of value (i.e.knows that 0.4 > 0.2)• Arranges four wholenumbers (up to 4 digits)and two decimal fractions(up to hundredths) in orderof value (i.e. knows that0.4 > 0.39)• Arranges four wholenumbers and 3 decimalfractions (up tothousandths) in order ofvalue• Arranges four integers(whole numbers and theiropposites) and threedecimal fractions (up tothousandths) in order ofvalue• Arranges four numbers ofany size in order of value• Expresses any natural(counting) number as aproduct of powers of primenumbers (e.g. the factortree for 36 000 is 2 5 x 3 2 x5 3 )• Places 1-digit numbers ona number line correctly• Uses non-standard andstandard place valuepartitions for 2 digitnumbers (e.g. 26 = 2 tens +6 ones, or 26 ones) anduses concrete materials todemonstrate thesegroupings• Places 2 and 1-digitnumbers on a number linecorrectly• Uses non-standard andstandard place valuepartitions for 3-digitcounting numbers (e.g.325 = 3 hundreds + 2 tens+ 5 ones, or 32 tens + 5ones, or 325 ones) anduses concrete materials todemonstrate thesegroupings• Places 1, 2, 3 digitnumbers on a number linecorrectly• Uses non-standard andstandard place valuepartitions for 3-digit wholenumbers (i.e. countingnumbers and zero) (e.g.405 = 4 hundreds + zerotens + 5 ones, or 40 tens +5 ones) and uses concretematerials to demonstratethese groupings• Uses place value tocompare and order wholenumbers to 3 digits andtenths, and locates them,relative to zero, on anumber line• Uses non-standard andstandard place valuepartitions for 4-digit wholenumbers and decimalfractions to hundredths;recognises differentrepresentations of numbersinvolving decimalfractions (e.g. 2.12, 2 +2/10, 2 + 0.1 + 2/100) andexplores related contextsinvolving money andmeasures (e.g. $2.12 and2.12 metres) and usesconcrete materials todemonstrate thesegroupings• Writes a decimal as afraction (e.g. 0.16 =16/100); counts forwardsand backwards in decimalfractions (e.g. says “zeropoint three eight, zeropoint three nine, zero pointfour zero – or zero pointfour”)• Uses skip counting to labela scale (e.g. marks from0 – 5 on a number line andcalibrates using 0.2, 0.4,0.6, 0.8, 1.0, 1.2…)• Knows the relationshipbetween decimal fractionsand money (i.e. knows that$2.43 is the same as twopoint four-three dollarswhich is “two dollars andforty three cents”)• Represents integers on anumber line anddetermines the differencebetween them as length(e.g. the distance between-3 and 2 is 5 units); orderrational numbers on asuitably scaled part of thereal number line• Explains why money andmeasures use decimalnotation (e.g. says “$5 and16 cents is written as $5.16and 5 m 16 cm is writtenas 5.16 metres becausethere are 100 cents in adollar and 100 cm in ametre• Represents any integersand halves and quarters(e.g. 2¾, -3½) on a numberline and approximationsfor some irrationalnumbers including0.333… and 0.666….)• Determines a decimalapproximation to a givendegree of accuracy in apractical situation (e.g.determines the side of asquare with area given insquare metres, to thenearest cm• Locates integers, decimals,fractions and decimalapproximations to someirrational numbers on thereal number line (e.g.3.5,-2/5, π ,√90)Bound for Success Scope and Sequence Statements V2 Page 30 Working Document Semester One 2007