Bound for Success Scope and Sequence Statements

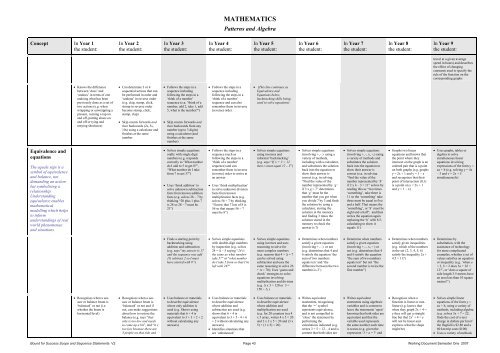
MATHEMATICSPatterns and AlgebraConcept In Year 1the student:In Year 2the student:In Year 3the student:In Year 4the student:In Year 5the student:In Year 6the student:In Year 7the student:In Year 8the student:In Year 9the student:travel at a given averagespeed in hours) and describesthe effect of changingconstants used to specify therule of the function on thecorresponding graphs• Knows the differencebetween ‘does’ and‘undoes’ in terms of oneundoing what has beenpreviously done as a set oftwo actions (e.g. whenwrapping or unwrapping apresent, turning a tap onand off, putting shoes onand off or tying anduntying shoelaces)• Can determine 3 or 4sequential actions that canbe performed in order and‘undone’ in reverse order(e.g. clap, stamp, click,stomp in reverse orderbecome stomp, click,stamp, clap)• Skip counts forwards andthen backwards (2s, 5s,10s) using a calculator andfinishes at the samenumber• Follows the steps in asequence includingfollowing the steps in a‘think of a number’sequence (e.g. “think of anumber, add 2, take 1, add5, what is the number?”)• Skip counts forwards andthen backwards from anynumber (up to 3 digits)using a calculator (andfinishes at the samenumber)• Follows the steps in asequence includingfollowing the steps in a‘think of a number’sequence and can alsoremember them in inverse(reverse) order• (This line continues asEquivalence andEquations below,backtracking skills beingused to solve equations)Equivalence andequationsThe equals sign is asymbol of equivalenceand balance, notdemanding an actionbut symbolising arelationship.Understandingequivalence enablesmathematicalmodelling which helpsto informunderstandings of realworld phenomenaeand situations.• Solves simple equationsorally with single digitnumbers (e.g. respondscorrectly to ‘What numberdo I add to 5 to get 8?”,“What number do I takefrom 7 to get 3?”)• Uses ‘think addition’ tosolve unknown subtractionfacts from known additionfacts (e.g. solves 28 – 7 bythinking “20 plus 1 plus 7is 28 so 28 – 7 must be21”)• Follows the steps in asequence (such asfollowing the steps in a‘think of a number’sequence) and canremember them in inverse(reverse) order to arrive atan answer• Uses ‘think multiplication’to solve unknown divisionfacts from knownmultiplication facts (e.g.solves 56 ÷ 7 by thinking“I know that 7 lots of 8 is56 so that means 56 ÷ 7must be 8”)• Solves simple equationsusing inverses andinformal ‘backtracking’(e.g. says “If ⌂ + 3 = 12then ⌂ must equal 12 – 3”)• Solves simple equations(involving +, - ) using avariety of methods,including with a calculator,and substitutes the solutionback into the equation toshow their answer iscorrect (e.g. in solving“Find the value of thenumber represented by ‘g’if 3 x g = 7” determinesthat ‘g’ must be thenumber that you get whenyou divide 7 by 3 and findsthe solution by using acalculator, storing thesolution in the memoryand finding 3 times thesolution stored in thememory to check theanswer is 7)• Solves simple equations(involving +, -, x, ÷,) usinga variety of methods andsubstitutes the solutionback into the equation toshow their answer iscorrect (e.g. in solving“find the value of thenumber represented by ‘h’if 2 x h – 3 = 11” solves byreading this as “two times‘something’, take three is11 so the ‘something’ takethree must be equal to fiveand a half. That means the‘something’, or ‘h’ must beeight and a half”, and thenwrites the equation againreplacing the ‘h’ with 8.5,calculating to show itequals 11)• Graphs two linearequations and knows thatthe point where theyintersect on the graph is anordered pair that is a pointon both graphs (e.g. graphsy = 2x + 1 and y = 1 – xand recognises that theirpoint of intersection (0,1)is a point on y = 2x + 1and y = 1 – x)• Uses graphs, tables oralgebra to solvesimultaneous linearequations involvingexpressions of the form y =ax + b (e.g. solving y = 4x– 3 and y = 2x + 5simultaneously)• Finds a starting point bybacktracking usingaddition and subtraction(e.g. says “my answer is 17and the sequence was add10, subtract 2 so I musthave started with 9”)• Solves simple equationswith double-digit numbersby inspection (e.g. solves24 = ∆ – 5 saying “24 isthe same as what numbertake 5?” or “what numberdo I take 5 from so that I’mleft with 24?”• Solves simple equationsusing inverses and usesreasoning to solve formore complex numbers(e.g. reasons that 4 + ∆ = 7can be solved usingsubtraction and uses thesame reasoning to solve 26+ ∆ = 70); Uses ‘guess andcheck’ strategies to solveequations involvingmultiplication and division(e.g. ∆ x 3 = 120 or 3 =150 ÷ ∆ )• Determines when numberssatisfy a given equation(involving +, - ) or not(e.g. determines that 4 and6 satisfy the equation ‘thesum of two numbersequals ten’ and ‘thedifference between the twonumbers is 2’)• Determine when numberssatisfy a given equation(involving +, -, x, ÷ ) ornot (e.g. determines that 4and 6 satisfy the equation“the sum of two numbersequals ten” but not “thesecond number is twice thefirst number”)• Determines when numberssatisfy given inequalities(e.g. which of the numbersin the set {2, 3, 4, 5, 6}satisfy the inequality 2x +4.5 > 11?)• Determines bysubstitution, with theassistance of technologyfor more complicatedexamples, whether a set ofvalues satisfies an equationor inequality (e.g. ‘when a= 3, b = 2 does 3a + 2b =12?’, or ‘does a square ofside length 3.5 metres havean area less than 10 squaremetres?’)• Recognises when a seesawor balance beam is‘balanced’ or not (i.e.whether the beam ishorizontal/level)• Recognises when a seesawor balance beam is‘balanced’ or not and ifnot, can make suggestionsabout how to restore thebalance (e.g. says “thatside is too low and needsto come up a bit”, and “it’stoo low because there are3 people on that side and• Uses balance or materialsto describe equivalencewhere only addition isused (e.g. Shows usingmaterials that 6 + 4 isequivalent to 3 + 3 + 2 + 2without calculating anyanswers)• Uses balance or materialsto describe equivalencewhere addition andsubtraction are used (e.g.shows that 6 + 4 isequivalent to 3 + 5 - 4 + 6+ 2 without calculating anyanswers)• Identifies situations thatare ‘unbalanced’• Uses balance or materialsto describe equivalencewhere addition andmultiplication are used(e.g. for 20 counters in a 4x 5 array, writes 4 x 5 = 20and 2 x 2 x 5 = 20 and (3 x5) + (1 x 5) = 20)• Writes equivalentstatements, recognisingthat the ‘=’ symbolrepresents equivalence,and is not compelled to‘close’ the statement byperforming thecalculations indicated (e.g.writes 3 + 5 = 12 – 4 and iscontent that both sides are• Writes equivalentstatements using algebraicvariables and is content toleave the statements ‘open’knowing that both sides areequivalent and that thevariable used representsthe same number each timeit occurs (e.g. given theexpression ‘3 + a = ?‘ and• Recognises when afunction is linear or nonlinear(e.g. knows thatwhen they graph 2x + 4 =y they will get a straightline but that 2x 2 + 4 = ywill not be linear andexplores what the shapemight be)• Solves simple linearequations of the form y =ax + b, using a variety ofmethods, including algebra(e.g. solves 3x + 7 = 22;finds the cost of a taxicharge in dollars per km ifthe flagfall is $2.80 and a60 km trip costs $100)• Uses a variety of methodsBound for Success Scope and Sequence Statements V2 Page 43 Working Document Semester One 2007