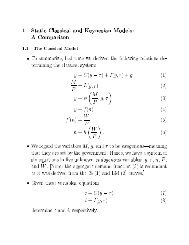1. Introduction - Econometrics at Illinois - University of Illinois at ...

Roger Koenker and Zhijie Xiao 11To test our hypothesis when is unknown, set (t) =(1;F ,10(t)) > and for anestimator ^ n satisfying,p n(^n , 0 )=set ~(t) =^ +^ 0 F ,10(t) =^ > n(t). Then(3.4)(3.5)Z 1^v n (t) = p n' 0 (t)(^(t) , ~(t)= 00h 0 (s)dv n (s)+o p (1)= p n' 0 (t)(^(t) , (t) , (~(t) , (t)))= 0= v n (t) , p n' 0 (t)(^ , 0 ) > (t)= 0Z 1= v n (t) , ' 0 (t)(t) > h 0 (s)dv n (s)+o p (1)Thus, if we take g(t) =(t; (t) > ' 0 (t)) > ,we obtain,_g(t) =(1; _ f=f;1+F ,10(t) _ f=f) >where _ f=f is evaluated at F ,10(t), so for example in the Gaussian case,_g(t) =(1; , ,1 (t); 1 , ,1 (t) 2 ) > :Given the representation (3.4) and the fact that (t) lies in the linear span of g, wemay again apply Khmaladze's martingale transformation to obtain,0~v n (t) =Q g^v n (t);which can then be shown to converge to the standard Brownian motion process. Aswe have suggested in Section 2, we would like to consider a two sampleversion of theforegoing problem in which weleave the precise functional form of the distributionF , and therefore the form of the function, g, unspecied under the null. As we havealready noted, this is a special case of the general quantile regression tests introducedin the next section.4. Quantile Regression InferenceThe classical linear regression model asserts that the conditional mean of the response,y i , given covariates, x i ,may be expressed as a linear function of the covariates.That is, there exists a 2 R P such that,E(y i jx i )=x > i :The linear quantile regression model asserts, analogously, that the conditional quantilefunctions of y i given x i are linear in covariates,(4.1)F ,1y i jx i(jx i )=x > i ()for in some index set T [0; 1]: The model (4.1) will be taken to be our basicmaintained hypothesis. For convenience we will restrict attention to the case that