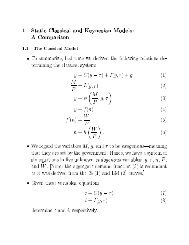1. Introduction - Econometrics at Illinois - University of Illinois at ...

Roger Koenker and Zhijie Xiao 7It is well known that v n (t) converges weakly to a Brownian bridge process, v 0 (t), thatis a mean-zero Gaussian process with covariance functionEv 0 (t)v 0 (s) =t ^ s , st;and thus the distribution of K n and related functionals follows from the observationof Doob (1949) and its subsequent renements.3.1. The Durbin Problem. It is rare in practice, however, that we are willing tospecify F 0 completely. More commonly, ourhypothesis places F in some parametricfamily F with 2 R p .For example, we may wish to test \normality", claimingthat Y has distribution F 0 (y) =((y , 0 )= 0 ), but 0 =( 0 ; 0 ) is unknown. Weare thus led to consider, following Durbin (1973), the parametric empirical process,U n (y) = p n(F n (y) , F^ n(y)):Again changing variables, so y ! F ,1 0(t); we may equivalently consideru n (t) = p n(G n (t) , G^ n(t))where G n (t) =F n (F ,1 0(t)) and G^ n(t) =F^ n(F ,1 0(t)) so G 0 (t) =t. Under mildconditions on the sequence f^ n g we have the linear (Bahadur) representation,p 1n(^n , 0 )=Zh 0 (s)dv n (s)+o p (1):0So provided the mapping ! G has a Frechet derivative, g = g 0 , that is,sup t jG +h (t) , G (t) , h > g(t)j = o(jjhjj) ash ! 0, see van der Vaart (1998, p.278),we maywrite,and thus obtain, with r n (t) =o p (1);(3.1)G^ n(t) =t +(^ n , 0 ) > g(t)+o p (1);^v n (t) = p n(G n (t) , t , (G^ n(t) , t))Z 1= v n (t) , g(t) > h 0 (s)dv n (s)+r n (t);which converges weakly to the Gaussian process,Z 1u 0 (t) =v 0 (t) , g(t) > h 0 (s)dv 0 (s):R The necessity of estimating 0 introduces the drift component g(t) > 1h 00(s)dv 0 (s):Instead of the simple Brownian bridge process, v 0 (t), we obtain a more complicatedGaussian process with covariance functionEu 0 (t)u 0 (s) =s ^ t , ts , g(t) > H 0 (s) , g(s) > H 0 (t)+g(s) > J 0 g(t)00