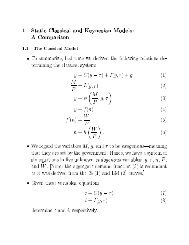1. Introduction - Econometrics at Illinois - University of Illinois at ...

More documents

Recommendations

Info

2 Inference on the Quantile Regression Processfunctions with techniques for estimating a full family of conditional quantile functions,quantile regression is capable of providing a much more complete statisticalanalysis of the stochastic relationships among random variables.There is already a well-developed theory of asymptotic inference for many importantaspects of quantile regression. Rank-based inference based on the approachof Gutenbrunner, Jureckova, Koenker, and Portnoy (1993) appears particularly attractivefor a wide variety ofquantile regression inference problems including theconstruction of condence intervals for individual quantile regression parameter estimates.There has also been considerable attention devoted to various resamplingstrategies. See e.g. Hahn (1995), Horowitz (1998), Bilias, Chen, and Ying (1999), Heand Hu (1999). In Koenker and Machado (1999) some initial steps have beentakentoward a theory of inference based on the entire quantile regression process. Thesesteps have claried the close tie to classical Kolmogorov-Smirnov goodness of t results,and related literature p-sample goodness-of-t tests based on Bessel processesinitiated by Kiefer (1959).This paper describes some further steps in this direction. These new steps dependcrucially on an ingenious suggestion by Khmaladze (1981) for dealing with tests ofcomposite null hypotheses based on empirical processes. Khmaladze's results wererather slow to percolate into statistics generally, but the approach has recently playedan important roleinwork on specication tests of the form of the regression functionby Stute, Thies, and Zhu (1998) and Koul and Stute (1999). In econometrics,Bai (1998) was apparently the rst to recognize the potential importance of thesemethods, considering tests of model specication based on the empirical process inparametric time series models.In contrast to the prior literature, which has focused on tests based directly onthe empirical process, we consider tests based on the quantile regression process. Wefocus primarily on tests of the hypothesis that the regression eect of covariates exertseither a pure location shift, or a location-scale shift of the conditional distribution ofthe response, versus alternatives under which covariates may alter the shape of theconditional distribution as well as its location and scale. These tests may beviewedas semiparametric in the sense that we need not specify a parametric form for theerror distribution.Khmaladze's martingale transformation provides a general strategy for purging theeect of estimated nuisance parameters from the rst order asymptotic representationof the empirical process and related processes and thereby restoring the feasibility of\asymptotically distribution free" tests. We will argue that the approach is especiallyattractive in the quantile regression setting and is capable of greatly expanding thescope of inferential methods described in earlier work. Although there are close formalconnections between the theory of tests based on the quantile regression processand the existing literature there are some signicant dierences as well. Some of thesedierences are immediately apparent from the classical Bahadur-Kiefer theorems and
Roger Koenker and Zhijie Xiao 3the literature on condence bands for QQ-plots, e.g. Nair (1982). But the principaldierences emerge from the regression specication of the conditional quantile functions.In particular, we introduce tests of the classical regression specications thatthe covariates aect only the location, or the location and scale, of the conditionaldistribution of the response variable without requiring a parametric specication ofthe innovation distribution.An alternative general approach to tests based on empirical processes with estimatedparameters entails resampling the test statistic under conditions consistentwith the null hypothesis to obtain critical values. The origins of this approach maybe traced to Bickel (1969). Romano (1988) describes implementations for a varietyof problems. Andrews (1997) introduces a conditional Kolmogorov-Smirnov test formodel specication in parametric settings and uses resampling to obtain critical values,and Abadie (2000) develops related methods for investigating treatment eectsin the two sample setting. We hope to explore this approach to quantile regressioninference in subsequent work.The remainder of the paper is organized as follows. In the next section, we introducea general paradigm for quantile regression inference focusing initially on thecanonical two-sample treatment-control model. In Section 3, we briey introduceKhmaladze's approach to handling empirical processes with estimated nuisance parameters.Section 4 extends this approach to general problems of inference basedon the quantile regression process. Section 5 treats some practical problems of implementingthe tests. Section 6 describes an empirical application to the analysis ofunemployment durations. Section 7 contains some concluding remarks.2. The Inference ParadigmTo motivate our approach it is helpful to begin by reconsidering the classical twosampletreatment-control problem. In the simplest possible setting we can imaginea random sample of size, n, drawn from a homogeneous population and randomizedinto n 1 treatment observations, and n 0 control observations. We observe a responsevariable, Y i , and are interested in evaluating the eect of the treatment on this response.In a typical clinical trial application, for example, the treatmentwould be some formof medical procedure, and Y i ,might be log survival time. In our application discussedin Section 6, the treatment is an oer of a cash bonus for early exit from a spell ofunemployment, and Y i is the logarithm of individual i's unemployment duration. Inthe rst instance we might be satised to know simply the mean treatment eect, thatis, the dierence in means for the two groups. This we could evaluate by \runningthe regression" of the observed y i 's on an indicator variable: x i = 1, if subject iwas treated, x i = 0, if subject i was a control. Of course this regression wouldpresume, implicitly, that the variability ofthetwo subsamples was the same; thisobservation opens the door to the possibility that the treatment alters other features
Page 1: INFERENCE ON THE QUANTILE REGRESSIO
Page 5 and 6: Roger Koenker and Zhijie Xiao 5We c
Page 7 and 8: Roger Koenker and Zhijie Xiao 7It i
Page 9 and 10: Roger Koenker and Zhijie Xiao 9Let
Page 11 and 12: Roger Koenker and Zhijie Xiao 11To
Page 13 and 14: Roger Koenker and Zhijie Xiao 13We
Page 15 and 16: Roger Koenker and Zhijie Xiao 15The
Page 17 and 18: Roger Koenker and Zhijie Xiao 17The
Page 19 and 20: Roger Koenker and Zhijie Xiao 19and
Page 21 and 22: and the transformed process isRoger
Page 23 and 24: Roger Koenker and Zhijie Xiao 23loc
Page 25 and 26: Roger Koenker and Zhijie Xiao 25Fig
Page 27 and 28: Roger Koenker and Zhijie Xiao 27as
Page 29 and 30: Roger Koenker and Zhijie Xiao 29for
Page 31 and 32: Roger Koenker and Zhijie Xiao 31thu
Page 33 and 34: ThusandZ _g n (s) > C n (s) ,1 Z 1R
Page 35 and 36: Roger Koenker and Zhijie Xiao 35App
Page 37 and 38: Roger Koenker and Zhijie Xiao 37TAB
Page 39: Roger Koenker and Zhijie Xiao 39(19

1. Introduction - Econometrics at Illinois - University of Illinois at ...

Create successful ePaper yourself

Delete template?

Save as template?