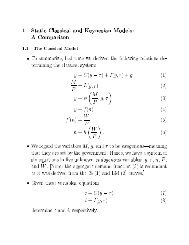1. Introduction - Econometrics at Illinois - University of Illinois at ...

and the transformed process isRoger Koenker and Zhijie Xiao 21~v() =w 0 ()+ ~ () 0 ,1=2x + o p (1)where the noncentrality process () ~ is simply the martingale transformation of() =' 0 ()F ,10(). Provided that () _ is not in the space spanned by the functionsf1; _' 0 ()g; it is clear that () ~ 6= 0, so the proposed tests have non-trivial power. Figure1 depicts the noncentrality function () its \predicted" version, and its (residual)transformed version () ~ for the normal case. For any given 0 ; the asymptotic localpower of the proposed Kolmogorov-Smirnov test is given as followsP (c) =Prsup2Tw 0 ()+ ~ () 0 ,1=2x >c where c is the asymptotic critical value at signicance level :Example. It is of obvious interest to consider alternatives for which the function 0 (t) =' 0 (t)F ,10(t) is annihilated by the martingale transformation. This entailsthat _ 0 (t) lie in the linear span of f1; _' 0 (t)g, and is evidently satised for F 0 uniform.More surprisingly, it is also satised for triangular densities like, f 0 =(1,jxj)I(jxj1). These cases may be regarded as somewhat pathological as they have inniteFisher information for both location and scale. Thus, it may not be regarded as toodisturbing that the transformation performs poorly under such circumstances.5.5. Extensions. The proposed methods can be easily modied to accommodatemany other inference problems, including tests for parametric conditional distributionsand tests for conditional symmetry. The theory wedevelop also carries over withminor changes to some analytic nonlinear restrictions in place of (4.4) and associatedchanges in the transformation (4.6). For example, we may modify our hypothesis tothe form(5.4)R() , r = (;):If were known, the previous tests would apply. More generally, if is unknown butmay be estimated by a p n consistent estimator, n ; then, under regularity conditions(so that admits a Taylor expansion to the second order), the standardized empiricalprocess R n ^() , rn , (; n ) has the following approximation^v n () = p n' 0 () R n R > n ,1=2R n ^() , rn , (; n )= v n ()+' 0 ()Z 1 + ' 0 ()F ,10()Z 2 + ' 0 ()s() > Z 3 + o p (1);where s() =@ (; 0 )=@; and Z j = O p (1), j =1; 2; 3: Denoting the set of linearlyindependent components of functions(;' 0 ();' 0 ()F ,10();' 0 ()s() > );