FIAS Scientific Report 2011 - Frankfurt Institute for Advanced Studies ...

Complete and Clustered Synchronization in Complex Networks
Collaborators: S. Becker 1 , M. Schäfer 1 , M. Greiner 2 , S. Schramm 1
1 Frankfurt Institute for Advanced Studies, 2 Department of Mathematics, Aarhus University, Denmark
We consider the dynamics of a complex network, consisting of N nodes and L links. The dynamics are given in
the following way: Each node is assigned a (for simplicity scalar) variable xi ∈ [−1,1], which evolves in time
according to
x t+1
i
= (1 − ε) f (xt i) + ε
N
∑ Ai jg(x
j=0
t j),
where f and g are bounded functions and Ai j is the adjacency matrix of the network (including suitable normalization).
More specifically, we are interested in almost bipartite networks in the sense that in addition to the bipartite
structure of links between two groups of nodes in a graph, there exist a few extra links within these two groups.
We call the links between the two clusters “inter-cluster links” and the links within a cluster “intra-cluster
links”. We look at the collective dynamics, i.e. the synchronization behavior of such systems. It has been noted
in numerical studies that the presence of additional intra-cluster links may lead to enhanced synchronization,
an analytical treatment of the problem is, however, still missing.
To investigate the synchronization behavior, we have analytically reformulated the problem in terms of a perturbed
master stability approach. Due to the presence of the non-bipartite links, this does not decouple into a
set of two-dimensional parametric equations, but remains N dimensional, however, since the coupling within
the two clusters is small, we hope that we may be able to treat the synchronization perturbatively.
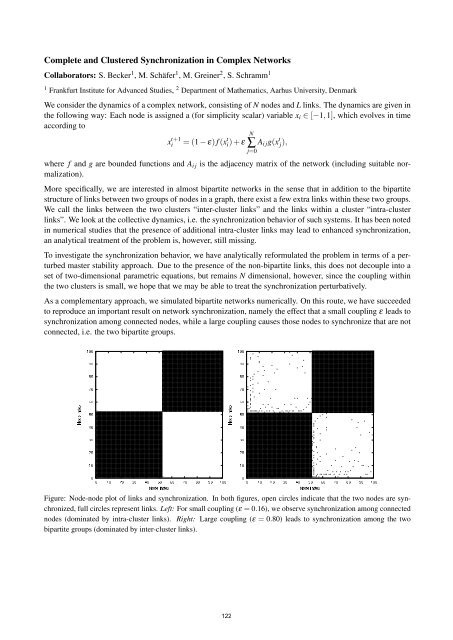
As a complementary approach, we simulated bipartite networks numerically. On this route, we have succeeded
to reproduce an important result on network synchronization, namely the effect that a small coupling ε leads to
synchronization among connected nodes, while a large coupling causes those nodes to synchronize that are not
connected, i.e. the two bipartite groups.
Figure: Node-node plot of links and synchronization. In both figures, open circles indicate that the two nodes are synchronized,
full circles represent links. Left: For small coupling (ε = 0.16), we observe synchronization among connected
nodes (dominated by intra-cluster links). Right: Large coupling (ε = 0.80) leads to synchronization among the two
bipartite groups (dominated by inter-cluster links).
122