Correction TD1.pdf - Les CPGE de Loritz

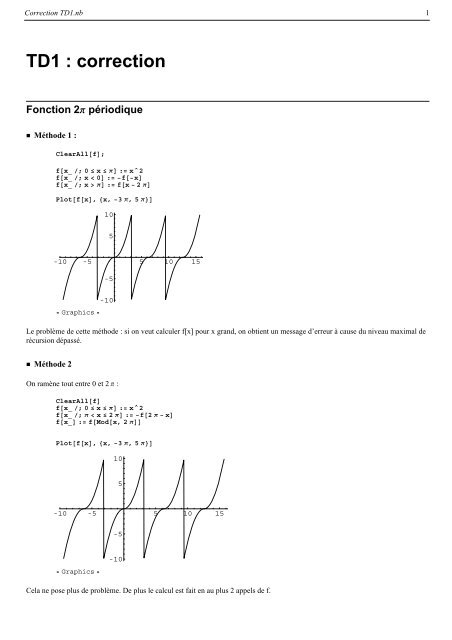
Correction TD1.nb 1TD1 : correctionFonction 2Π périodique Méthode 1 :ClearAllf;fx_ ; 0 ≤ x ≤ Π :⩵ x^2fx_ ; x 0 :⩵ fxfx_ ; x Π :⩵ fx 2ΠPlotfx, x, 3Π, 5Π105-10 -5 5 10 15-5 Graphics -10Le problème de cette méthode : si on veut calculer f[x] pour x grand, on obtient un message d’erreur à cause du niveau maximal derécursion dépassé. Méthode 2On ramène tout entre 0 et 2Π :ClearAllffx_ ; 0 ≤ x ≤ Π :⩵ x^2fx_ ; Π x ≤ 2Π :⩵ f2Π xfx_ :⩵ fModx, 2ΠPlotfx, x, 3Π, 5Π105-10 -5 5 10 15-5 Graphics -10Cela ne pose plus de problème. De plus le calcul est fait en au plus 2 appels de f.

Correction TD1.nb 2DL de SinL ⩵ TableNormalSeriesSinx, x, 0, k, k, 1, 9, 2x, x x36 , x x36 x5120 , x x36 x5120 x75040 , x x36 x5120 x75040 x9362880 L ⩵ AppendL, Sinxx, x x36 , x x36 x5120 , x x36 x5120 x75040 , x x36 x5120 x75040 x9362880 , SinxPlotEvaluateL, x, 0, Π,PlotStyle EvaluateTableDashingk, k, k, 0, 0.025, 0.0051.510.50.5 1 1.5 2 2.5 3 Graphics Suites récurrentes doubles :u0 ⩵ 1; v0 ⩵ N 2, 50;un_Integer :⩵ un 1 vn 1vn_Integer :⩵ un 1 vn 1 2∆n_Integer :⩵ vn un;On regarde les premières valeurs de ∆ :Tablen, ∆n, n, 0, 6 TableForm0 0.41421356237309504880168872420969807856967187537691 0.01789966618382645768334439154437312399186384522472 0.00003342660151417295258659451251002659689077666793 1.165700032844950808866067552586277708850 10 104 1.4176727055604162678639464894 10 215 2.096787 10 436 0. 10 50La convergence est plutot rapide... on obtient donc une valeur approchée de la limite à 5 chiffres pour n=3 et à 10 pour n=4 (on l’ameme à 20 chiffres).

Correction TD1.nb 3u31.19814023467730720579838378818980070873183085585721u41.19814023473559220743921365592754367009328079481030DL à l’ordre le plus élevé possibleClearAllf, G, gfx_ :⩵ Sinhx a x b x^3 c x^5 1 d x^2 e x^4Gn_Integer :⩵ Seriesfx, x, 0, n Méthode 1 :On extrait les coefficients, on crée une liste d’équations en prenant les coefficients de degré impair, puis on résout :Listen_Integer :⩵ TableSeriesCoefficientGn, k 0, k, 1, n, 2Liste51 a 0, 16 b a d 0, 1120 c b d a d2 a e 0SolveListe7Solve::svars : Equations may not give solutions for all "solve" variables. Plus…c 1 4203 49 d, e 1840Sol ⩵ SolveListe9c 1 42 d, b 1 1 6 d, a 16551166320 , b 53396 , e 513 , a 1, d 11088 396 SolveListe11gx_ :⩵ fx . SolPlotgx, x, 0, 1, PlotRange 0, 0.000000022·10 -81.75·10 -81.5·10 -81.25·10 -81·10 -87.5·10 -95·10 -92.5·10 -90.2 0.4 0.6 0.8 1 Graphics Méthode 2La meme chose en plus rapide :

Correction TD1.nb 4SolveAlwaysG9 0, xc 551166320 , b 53396 , e 513 , a 1, d 11088 396 SériesPuisque n 6 3n 2 16 est équivalent à n en +∞, il faut que P(n) soit équivalent à n 3 en +∞.In[1]:=Px_ :⩵ x^3 a x^2 b x cIn[3]:=In[6]:=Out[6]=In[8]:=un :⩵ n^6 3n^2^1 6 Pn^1 3S ⩵ Seriesun, n, ∞, 2 a a 23 9 b3n 5 a381 2 a b9 c 3 1n 2 O 1SolveSeriesCoefficientS, 0 0, SeriesCoefficientS, 1 0, a, b, cn 3Solve::svars : Equations may not give solutions for all "solve" variables. Plus…Out[8]=b 0, a 0Fonction et fonction réciproqueIn[9]:=In[10]:=In[13]:=ClearAllf, xfx_ :⩵ Log1 x x x^2Plotfx, x, 1, 3, PlotRange 0, 332.521.510.5Out[13]=-1 1 2 3 Graphics Les racines du dénominateur sont 0 et −1. Donc f est définie pour x>1 et x≠0.In[17]:=Limitfx, x 0Out[17]= 1In[18]:=Out[18]=In[19]:=f’x11 x x x 2 Limitf’x, x 01 2 x Log1 x x x 2 2Out[19]= 3 2

Correction TD1.nb 5In[20]:=Plotf’x, x, 1, 3, PlotRange 5, 542-1 1 2 3-2-4Out[20]=In[28]:=Out[28]= Graphics gx_ ⩵ Simplifyf’x x x^2^2x 1 2 x Log1 xf’ et g sont de meme signe, il suffit donc d’étudier gIn[24]:=In[38]:= Algebra‘InequalitySolve‘Plotgx, x, 1, 3-1 1 2 3-2-4-6-8Out[38]=-10 Graphics In[42]:=Out[42]=g’xg’’x1 1 2 x 2 Log1 x1 xOut[43]= 41 x 1 2 x1 x 2In[39]:=Out[39]=InequalitySolveg’’x 0, x 1, xx 1g est donc strictement concave et g’ est strictement décroissante.In[40]:=g’0Out[40]= 0Donc g’ est positive avant 0 et négative après.In[41]:=g0Out[41]= 0Donc g reste négative et f est décroissante sur son ensemble de définition.

Correction TD1.nb 6In[49]:=ParametricPlott, ft, ft, t, t, t,t, 1, 3, PlotRange 1, 3, 1, 3, AspectRatio 132.521.510.5-1 -0.5 0.5 1 1.5 2 2.5 3-0.5Out[49]=In[52]:=Out[52]=In[54]:=Out[54]=In[56]:=-1 Graphics S ⩵ Seriesfx, x, 0, 51 3 x 2 11 x2625 x3 12T ⩵ InverseSeriesS, x2 x 1 3 44 81 x 12 ComposeSeriesT, S137 x4 6049 x5 Ox2061036 x 13 2187126176 x 14 2952453136664 x 15 Ox 179716156Out[56]= x Ox 6Rapidité de convergenceIn[69]:=In[70]:=In[71]:=Out[71]=In[72]:=ClearAllf, G, x, nGn_ :⩵ NormalSeriesArcSinx, x, 0, nG4x x36Valn_ :⩵ 6 Gn . x 1 2Val10Out[74]= 3.14151In[80]:=In[81]:=Decimalesn_ :⩵ FloorLog10, AbsValn ΠDecimales10Out[81]= 4

Correction TD1.nb 7In[84]:=ListPlotEvaluateTableDecimalesn, n, 1, 501512.5107.552.510 20 30 40 50Out[84]= Graphics Une suite bizarre Une première méthodeIn[85]:=un_Integer :⩵ Whichun 1 1, 1, EvenQun 1, un 1 2, OddQun 1, 3 un 1 1In[98]:= Gh_Integer, iter_Integer :⩵u0 ⩵ h; ListPlotTableun, n, 0, iter, PlotJoined TrueIn[99]:=G5, 10161412108644 6 8 10Out[99]= Graphics In[100]:=G12, 121512.5107.552.5Out[100]= Graphics 2 4 6 8 10 12

Correction TD1.nb 8In[101]:=G17, 205040302010Out[101]= Graphics 5 10 15 20 Une méthode plus élégante :Plutot que de calculer et recalculer plusieurs fois les termes, on peut les memoriser, ou meme construire la liste des termesconsecutifs :In[103]:=Fn_ :⩵ Whichn 1, 1, EvenQn, n 2, OddQn, 3n 1In[121]:=Hdepart_, iter_ :⩵L ⩵ depart; Fori ⩵ 0, i iter, i, L ⩵ L . y___, x_ y, x, Fx; LIn[123]:=H17, 20Out[123]=17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1La méthode : on part d’une liste avec le premier élément et par itération, on remplace la liste par elle−meme plus l’image dudernier élément.In[128]:=ListPlotH117, 30, PlotJoined True10080604020Out[128]= Graphics 5 10 15 20 25 30La conjecture de Syracuse est que quel que soit le terme initial la suite devient stationnaire, égale à 1.