Serie Storiche e Processi Stocastici

Introduzione
Serie Storiche e Processi Stocastici – Federico Andreis
Desiderando introdurre intuitivamente il concetto di serie storica basta fare riferimento a
qualsiasi fenomeno misurabile che varia nel tempo e la cui registrazione costituisce, appunto, la
serie storica. Tale successione di dati rappresenta una informazione statistica sulla quale potremmo
avere interesse, oltre che nel descrivere, anche nell‟inferire (ovvero all‟applicare gli strumenti
propri dell‟analisi statistica con scopi di previsione).
Più precisamente, per serie storica o serie temporale intendiamo una successione di
osservazioni ordinate logicamente secondo una variabile t, la quale nella maggior parte dei casi
rappresenta il tempo. Risulta quindi di interesse lo studio della dinamica temporale di tale serie
(analisi univariata) e delle eventuali connessioni con altre serie storiche ad essa collegate (analisi
multivariata). Confluiscono in questa analisi gli strumenti e i contributi della statistica, del calcolo
della probabilità, dell‟econometria e dell‟analisi matematica.
Per questa trattazione le nozioni richieste in questi campi sono quelle di base di normali corsi
universitari di analisi matematica, statistica descrittiva e inferenziale e qualche conoscenza di
calcolo delle probabilità, principalmente con riguardo alle variabili casuali.
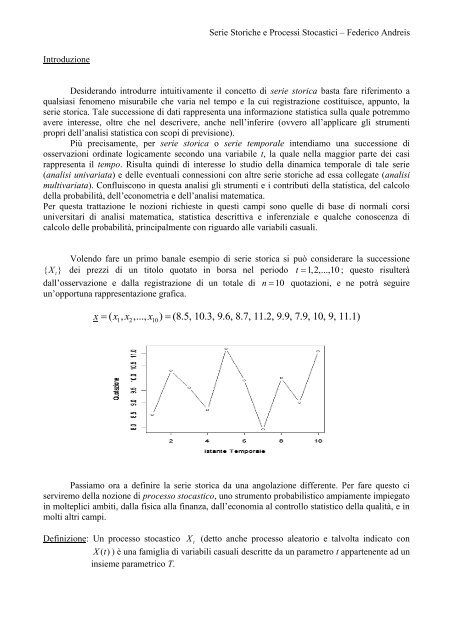
Volendo fare un primo banale esempio di serie storica si può considerare la successione
{ X t}
dei prezzi di un titolo quotato in borsa nel periodo t 1,2,...,10 ; questo risulterà
dall‟osservazione e dalla registrazione di un totale di n 10 quotazioni, e ne potrà seguire
un‟opportuna rappresentazione grafica.
x ( x , x ,..., x ) (8.5, 10.3, 9.6, 8.7, 11.2, 9.9, 7.9, 10, 9, 11.1)
1 2 10
Passiamo ora a definire la serie storica da una angolazione differente. Per fare questo ci
serviremo della nozione di processo stocastico, uno strumento probabilistico ampiamente impiegato
in molteplici ambiti, dalla fisica alla finanza, dall‟economia al controllo statistico della qualità, e in
molti altri campi.
Definizione: Un processo stocastico X t (detto anche processo aleatorio e talvolta indicato con
Xt () ) è una famiglia di variabili casuali descritte da un parametro t appartenente ad un
insieme parametrico T.

Serie Storiche e Processi Stocastici – Federico Andreis
Cosa significa tutto questo? Significa che un processo stocastico è una successione di
variabili aleatorie ordinate secondo un parametro t T , solitamente identificato con il tempo. La
conoscenza di un processo stocastico equivale alla conoscenza della distribuzione di probabilità
multipla (multivariata) per qualsiasi sottoinsieme di T e per qualsiasi valore delle variabili casuali.
Occorre caratterizzare però ulteriormente questa nozione di processo stocastico; per fare
questo introduciamo delle distinzioni. Parleremo di processo stocastico continuo qualora le variabili
casuali che lo compongono siano di natura continua, di processo stocastico discreto in caso
contrario; distingueremo inoltre fra processi stocastici a tempo continuo e a tempo discreto, nei casi,
rispettivamente, che il parametro t T abbia supporto continuo o discreto.
Esempio: sia X t un processo stocastico che descrive le rilevazioni negli istanti temporali
tT {1,2,3,...} di una qualche grandezza fisica e le cui realizzazioni siano
caratterizzate da leggi di distribuzione gaussiane. Allora il processo in esame sarà da
definirsi come processo stocastico continuo a tempo discreto.
Un tale processo è quindi la famiglia di variabili casuali { X1, X 2,...}
, per la cui conoscenza
occorre specificare le funzioni di densità congiunte di ciascuna combinazione di esse. Formalmente
un processo t X è noto se è nota la funzione di densità ( Xt , X ,..., )
1 t X 2 t per ogni k e per ogni k-pla
k
di valori ( t1, t2,..., t k ) di variabili casuali (d‟ora in poi v.c.). Da questo si può già intuire l‟estrema
complicazione dello studio di un processo stocastico nella sua generalità, e in particolare la pratica
impossibilità di inferire direttamente su di esso.
Volendo descrivere meglio la struttura probabilistica di X t possiamo osservare che, per
esempio, fissando t 3,
si ottiene la v.c. X 3 , che possiede una sua propria funzione di densità di
probabilità (nel caso continuo, di massa di probabilità nel caso discreto) che sarà correlata oppure
no alle altre, e così via. Su X 3 possiamo effettuare un esperimento e rilevare dei valori appartenenti
al suo campo di variazione.
Estendendo a tutto il processo, se fissiamo una prova da effettuare su X t (ovvero
osserviamo la successione dei risultati campionari x1, x 2,...
) otterremo una successione di valori,
funzione della variabile t, chiamata realizzazione o traiettoria del processo. Risulta evidente che,
dato un processo X t , esistono infinite possibili realizzazioni che sono precisamente tutte quelle
osservabili ripetendo indefinitamente l‟esperimento. Segue un esempio grafico di due realizzazioni
campionarie dal medesimo processo.

Serie Storiche e Processi Stocastici – Federico Andreis
Infine, se in X t fissiamo t e contemporaneamente fissiamo la prova sperimentale (per
esempio fissiamo t 3 ed osserviamo il valore risultante per X 3 ) otteniamo, ovviamente, un
numero reale: cioè il valore realizzato per la v.c. fissata, ovvero il valore della realizzazione al
tempo t fissato.
Possiamo quindi introdurre a questo punto l‟intendimento di serie storica { x , t 1,2,..., N}
come una parte finita di una realizzazione di un processo stocastico X t .
Tale definizione concorda con quella fornita nell‟introduzione di serie storica come
“successione di osservazioni ordinate logicamente secondo una variabile t” e qualifica inoltre in
senso probabilistico la natura dei problemi che ci proponiamo di affrontare. Per esempio la
previsione di un valore del fenomeno in esame al tempo t N 1 note che siano le osservazioni
fino a t N diventa uno specifico problema di Calcolo delle Probabilità. Cioè: qual è la probabilità
X assuma un determinato valore (e qui entra, ad esempio, la teoria dei test statistici)
che la v.c. N 1
se su tale variabile si hanno informazioni derivate dall‟insieme di v.c. ( X1, X 2,...,
X N ) che hanno
generato la realizzazione finita ( x1, x2,..., x N ) .
Si noti d‟altro canto che una simile definizione mette in luce anche la limitazione delle
informazioni sul processo le quali sono, in generale, desumibili dalla conoscenza della serie storica.
Difatti essa non è altro che una parte finita di una singola realizzazione del processo; ci troviamo
quindi a lavorare non solo con un campione unico della famiglia delle v.c. che caratterizzano il
processo, ma si tratta anche di un campione troncato, poiché si osserva solo per t 1,2,..., N.
Tutto
questo impone quindi una limitazione della classe dei processi stocastici, perché solo per una parte
più ristretta di essi sarà possibile dedurre informazioni “consistenti” dalle realizzazioni finite di cui
disponiamo nelle applicazioni reali.
Passiamo ora ad analizzare in modo più formale i processi stocastici e le loro
caratterizzazioni fondamentali.
t

Processi Stocastici
Serie Storiche e Processi Stocastici – Federico Andreis
Rifacendoci alla definizione presentata nell‟introduzione di processo stocastico, andiamo a
fornirne ora una sorta di classificazione, sulla base delle v.c. componenti un processo e dei loro
legami.
Una prima distinzione può essere fatta con riguardo all‟indipendenza o meno delle v.c.
componenti il processo. Tale stato difficilmente si riscontra nella realtà, l‟unico processo a
componenti incorrelate che tratteremo sarà il processo definito White Noise (rumore bianco) di
valor medio nullo e varianza costante (cioè non dipendente da t). In seguito verrà indicato con
A t e siglato con
2
t (0, A)
2
A
A WN . Un processo stocastico WN è quindi caratterizzato come segue:
EA ( ) 0
t
E( A ) Var( A )
2 2
t t A
0
t s
Cov( At , As ) E( At , As
) 2
A t s
Non vengono fatte a priori ipotesi sulla distribuzione di A1, A 2,...
, ma qualora si supponga
che, per ogni t, A t sia anche una v.c. Normale, allora si parla di Processo White Noise Gaussiano.
Poiché l‟incorrelazione di v.c. Normali implica l‟indipendenza, un processo WN Gaussiano è a
componenti indipendenti.
Una seconda distinzione riguarda la legge di probabilità delle v.c. componenti. Possiamo
infatti ipotizzare una prefissata funzione di densità (nel caso continuo) per tali variabili e definire di
conseguenza il processo risultante (un risultato teorico noto come Teorema di Kolmogorov ci
garantisce che, per ogni n intero, note che siano le densità di probabilità n-variate
f ( x , x ,..., x ; t , t ,..., t ) , il processo stocastico è completamente caratterizzato). L‟ipotesi più
1 2 n 1 2 n
comune è quella di suppore che le v.c. ( Xt , X ,..., )
1 t X 2 t costituiscano una variabile aleatoria
k
Multinormale per ogni ( t1, t2,..., t k ) e per ogni k 1.
In tal caso il processo stocastico X t si
definisce processo Gaussiano e possiede funzione di densità multivariata
f ( x , x ,..., x ) (2 ) exp ( x ) ( x )
1 2
k
2
N 1 1
2
2 1
x t t t t t
dove ( EX ( )) è il vettore dei valori medi e [ Cov( X , X )] la matrice delle varianze e
t ti
ti tj
covarianze del processo.
E‟ interessante soffermarsi sul fatto che un processo Gaussiano è caratterizzato solo da t e
e quindi, per esempio, un processo Gaussiano di valore medio 0 per ogni t è caratterizzato
esclusivamente dalla matrice delle varianze e covarianze delle v.c. X , X componenti il
ti tj
processo. Questa osservazione è di particolare rilievo perché ci dice che in una classe particolare e
limitata di processi stocastici (quella Gaussiana ad esempio) la conoscenza del processo stocastico
(e quindi di tutte le funzioni del processo) può essere ricondotta alla conoscenza di una particolare
categoria di funzioni (quali possono essere i momenti misti ad esempio), a loro volta stimabili dalle
realizzazioni finite (e quindi dalle serie storiche).
Altre distinzioni possono essere fatte con riguardo al comportamento della successione di
v.c. rispetto al parametro t. Si tratta dunque di andare a vedere se le variabili risultino o meno in un

Serie Storiche e Processi Stocastici – Federico Andreis
qualche equilibrio dinamico rispetto al tempo, in termini di valore atteso, di varianza, di entrambi o
di altre misure ancora. Se un processo stocastico X t presenta una distribuzione di equilibrio quando
t , ovvero sul piano delle realizzazioni è presente una certa “omogeneità temporale” di natura
stocastica, allora potremo parlare di processo stocastico stazionario.
Più precisamente parleremo di processo stocastico stazionario in senso stretto o forte
qualora la distribuzione multivariata delle v.c. ( Xt , X ,..., )
1 t X 2 t non sia funzione di ( t k
1, t2,..., t k )
per ogni k 1.
Formalmente:
( X , X ,..., X ) ( X , X ,..., X ) ( t , t ,..., t ) e j
t1 t2 tk t1 j t2 j tk j 1 2 k
Ne consegue, per k 1,
che XtXt j , e quindi tutte le “marginali” del processo sono
identicamente distribuite, da cui avranno uguale media e varianza
2
Var( Xt ) , t .
EX ( t ) ,
Analogamente, per k 2 , ( X , X ) ( X , X )
t t t jt j . La distribuzione congiunta dipende
1 2 1 2
solamente da t2 t1
e non dalla traslazione j. E così via crescendo in dimensione.
Ne consegue che se si considerano le componenti ( Xt, Xt h)
, ed esistono i momenti fino al secondo
ordine, la covarianza dipende solo da h:
Cov( X , X ) E[( X E( X ))][( X E( X ))]
t th t t th th E[( X )( X )]
h
t th Per h 0 la covarianza coincide con la varianza di t X
2
0 Cov( Xt , Xt ) Var( Xt
)
Le covarianze di un processo stocastico stazionario in senso stretto sono funzioni di h 0, 1, 2,... .
La funzione h appena introdotta viene denominata funzione di autocovarianza del processo
ed è una funzione simmetrica, infatti
Cov( X , X ) Cov( X , X )
h t th th t
Cov( X s, X sh ) h
(posto t h s )
Si definisce analogamente anche una funzione di autocorrelazione come segue:
{ : h 0, 1, 2,...}
h
Cov( X , X )/[ Var( X ) Var( X )]
h t thtth ( )
12
h 0 0 h 0
Ed essendo inoltre 0 1 ed ancora h h.
1
2

Serie Storiche e Processi Stocastici – Federico Andreis
La verifica dell‟ipotesi di stazionarietà in senso stretto è nella maggior parte dei casi reali
quasi impossibile, ci si limita dunque spesso a controllare che siano verificate delle condizioni
meno forti e riguardanti solo i momenti fino al secondo ordine (media, varianza, covarianza). Un
processo che rispetti tali proprietà è definito processo stocastico stazionario in senso lato o debole.
Generalmente si considera solo quest‟ultimo tipo di stazionarietà nelle applicazioni, riconducendo
la verifica alle proprietà di media, varianza e autocovarianza. In particolare diremo che un processo
è stazionario in senso lato se verifica le seguenti condizioni:
1. EX ( t ) , per ogni t
2. EX (
2
) 2
, per ogni t
t
3. E[( Xt )( X s )] st , per ogni coppia ( ts , )
La prima condizione richiede che il valor medio del processo sia costante e pari a al
2
finita e costante al variare di t;
variare di t; la seconda impone che il processo abbia varianza
l‟ultima condizione infine implica che per ogni t e s esista la funzione di autocovarianza fra le
variabili t X e X s . Tutto questo implica l‟esistenza dei momenti fino al secondo ordine, ma non
viene imposta alcuna condizione necessaria sulle funzioni di densità multivariate che caratterizzano
il processo X t . Da questo discende che mentre la stazionarietà in senso stretto implica, quando
esistano i momenti fino al secondo ordine, quella in senso lato, non vale il contrario.
Per quale motivo nella pratica risultano solitamente sufficienti le condizioni deboli di
stazionarietà del processo? Questo è giustificato dal ruolo fondamentale giocato dalla distribuzione
Normale nello studio di molti fenomeni fisici e naturali, per i quali è valido il Teorema del Limite
Centrale: dal momento che, sotto ipotesi di gaussianità, le condizioni di stazionarietà debole sono
sufficienti per avere anche la stazionarietà in senso forte, questo garantisce di potere evitare la
complicata (quando non impossibile) verifica in molteplici situazioni.
Un‟altra proprietà che, come le precedenti, un processo può possedere o meno, è
l‟invertibilità. Si tratta della possibilità di esprimere un processo X t tramite le v.c. precedenti
secondo l‟ordine logico imposto dal parametro t (e quindi ad esempio precedenti temporalmente);
formalmente significa che esistono una funzione lineare h () ed un processo WN A t tali che, per
ogni t, sia possibile scrivere
X h( X , X ,...) A
t t1 t2 t
Quindi la funzione h () collega X t con le variabili X s ( s t)
, e a tale relazione si aggiunge il
processo A t per rendere la stocasticità il processo (in assenza si tratterebbe né più né meno che di
una funzione deterministica di t). L‟invertibilità diventa particolarmente rilevante nello studio di
alcuni modelli che presenteremo in seguito, ma già da qui si può intuire come possa risultare
importante in un‟ottica di previsione, in effetti si tratta della possibilità di regredire il nostro
processo stocastico sui suoi valori passati.
Esiste anche un‟altra classificazione che distingue i cosiddetti processi periodici.
Formalmente diremo che X t è un processo periodico se esiste un valore s tale che, per ogni t
Pr{ Xt Xts}
1

Serie Storiche e Processi Stocastici – Federico Andreis
Dunque un processo periodico si ripete identicamente dopo s unità temporali. Se questo s è
esattamente parti all‟anno solare ( s 1 per dati annuali, s 2 per dati semestrali, s 4 per dati
trimestrali, e così via) allora diremo che il processo periodico è stagionale.
Esistono altri tipi di classificazione di cui non tratteremo, ad eccezione della proprietà di
ergodicità che verrà presentata in seguito. Tutte queste definizioni fanno riferimento ai processi
stocastici e non alle serie storiche, che ne costituiscono solo una realizzazione finita. Si consideri
però che serie storiche stazionarie sono quelle generate da processi stazionari e che processi
gaussiani producono realizzazioni finite che, statisticamente, possono essere ben approssimate da
distribuzioni Normali, e così via. Tranne l‟invertibilità (che è soprattutto una caratteristica teorica
che viene resa operativa dal problema della previsione) le condizioni di stazionarietà e Normalità
del processo sono in genere agevolmente deducibili dalle serie storiche osservate.
Verifica di Stazionarietà (debole) di un Processo
La funzione di autocovarianza introdotta precedentemente ci fornisce uno strumento teorico
per verificare se un processo stocastico X t sia stazionario o meno. Tale procedura può essere
applicata ai dati della serie storica che noi supponiamo essere la realizzazione finita del processo.
La verifica si articola nei seguenti tre passi:
1. Verificare che il valor medio di X t non dipenda da t
2. Calcolare 0 , ovvero Var( X t ) e verificare che sia finita
3. Verificare che h , per h 1,2,... sia una funzione solo di h e non di t
L‟autocovarianza misura il segno e l‟intensità del legame lineare che intercorre fra X t e
X t hal
variare di h; dunque esprime le connessioni fra le v.c. che compongo il processo stocastico
al variare della distanza tra di esse.
D‟ora in avanti considereremo soddisfatta l‟ipotesi di stazionarietà, la quale verrà sottintesa
e non più ovunque specificata.
Nell‟ottica di poter effettuare dei confronti fra più processi stocastici risulta più comodo
affidarsi alla funzione di autocorrelazione la quale ha un campo di variazione ben definito, a
differenza di quella di autocovarianza che ha come dominio tutto il campo reale. Richiamiamo
quindi tale funzione già definita in precedenza come
{ : h 0, 1, 2,...}
h
Cov( X t, X th )
h
Var( X ) Var( X )
h h
0 0
t th 0

Serie Storiche e Processi Stocastici – Federico Andreis
Questa funzione possiede proprietà notevoli, le più importanti delle quali sono:
1. 0 1
Si tratta infatti di fare il rapporto tra 0 e sé stesso, inoltre 0 è il coefficiente di
correlazione di X t con sé stesso.
2. h h, per ogni h 0,1,2,...
Difatti, come dimostrato in precedenza, h h per la simmetria della covarianza.
3. h 1,
per ogni h 0,1,2,...
Da un punto di vista statistico, sappiamo che la correlazione è definita nel dominio [ 1,1] .
4. ( aX b) ( X ) , per ogni h 0,1,2,... e per qualsiasi coppia reale ( ab , )
h t h t
Questo poiché essendo
proprietà della covarianza, e dal momento che
proprietà di cui sopra.
Cov aX b aX b a Cov X X a X per le
( t , th) 2
( t, th) 2
h( t )
Var( aX t b) 2
a Var( Xt )
2
a 0(
X t )
segue la
5. La matrice di Toeplitz di ordine m associata alla funzione di autocorrelazione di un
processo stazionario è definita positiva.
Ricordiamo brevemente che la matrice di Toeplitz di ordine m, associata a h , è definita per
ogni m 1,2,3,... come
1 1 2 ... m1
1 ...
1 1 m2
2 1 1 ... m3
P( m) [ ], ( i, j) 1,2,..., m
ij
. . . ... .
. . . ... .
... 1
m1 m2 m3
Si tratta quindi di una matrice simmetrica contenente i valori della funzione di
autocorrelazione fino all‟ordine m 1.
Commentiamo brevemente queste proprietà: la 1. e la 3. affermano che la funzione di
autocorrelazione è normalizzata ad 1 e che questo massimo è raggiunto per h 0 . La 2. mostra
che h è simmetrica, per cui la sua analisi viene sempre intrapresa per valori di h positivi. La
proprietà 4. esplicita che l‟autocorrelazione è invariante per traslazione e cambiamento di scala,
per cui un processo X t può essere studiato sotto l‟unità di misura di volta in volta più

Serie Storiche e Processi Stocastici – Federico Andreis
conveniente. La 5. enuncia una serie di condizioni necessarie e sufficienti affinché una
{1, , ,..., ,...} sia effettivamente la funzione di autocorrelazione di un processo
successione 1 2
m
stazionario. In altri termini, mentre è necessario che sia verificata la 3. per ogni h affinché h
sia una funzione di autocorrelazione, solo la condizione che la matrice di Toeplitz sia definita
positiva per ogni m garantisce che esista un processo stazionario X t che possegga
{ h, 0,1,2,...} h come propria funzione di autocorrelazione. Come è noto una matrice è
definita positiva se e solo se tutti i minori principali di qualsiasi ordine sono positivi; svolgendo
P definita sopra si nota per m 1,2 non risultano particolari
i calcoli sulla generica matrice ( m)
limitazioni sulla funzione h , mentre invece per m 3 discendono condizioni particolarmente
restrittive. In effetti
P
(1)
10 1
1 0 1 1
1 2
(2) 11 1
1
P
1
1 2
(3) 1 1 2 2 2
1
P
1 (1 )(1 2 ) 0
2 1
1
121
2
2
21 1
E così via per P( ) 0, m
4,5,... . Si nota quindi subito come, mentre per i primi due
m
ordini le condizioni sono banali o ricalcano altre proprietà, già da m 3 la questione si fa più
complicata. La soluzione della disuguaglianza porta ad un vincolo ben preciso, che restringe in
modo consistente lo spazio di definizione della funzione h (per essere precisi lo restringe
esattamente da un‟area di definizione pari a 4 ad una di 10/3, riducendolo quindi di 1/6; per
rendersene conto basti disegnare negli assi cartesiani ( xy , ) ( 2, 1)
le condizioni per m 2 e
m 3,
ne risulterà un quadrato di lato 2 avente baricentro nell‟origine ed una parabola di vertice
(0, 1) che porta l‟area di definizione a coincidere con la sua intersezione con il quadrato.
Per fare un esempio numerico ed intuitivo, se 1 1 2 0,7071
, allora 2 0 (poiché
dalle condizioni per 3
m risulta che dovrà aversi 2
2
2 1 2 1 2 1 2 2 1 0).
2 1
Questo è senz‟altro notevole ma risulta comunque ragionevole con riguardo all‟aspettativa che
se la correlazione fra t X e X t
1 (a distanza di una unità temporale l‟una dall‟altra, o 1 lag) è
così elevata (circa 70,71%) risulta ragionevole pensare che la correlazione fra t X e X t
2
(distanti 2 lags) non può essere negativa; questo perché il processo in esame possiede quella
omogeneità temporale che abbiamo identificato come la stazionarietà.
Portiamo ora un semplice esercizio che serva ad applicare le nozioni finora acquisite. Sarà
dato un processo stocastico e dovremo verificarne la stazionarietà e costruirne la matrice di
Toeplitz.

Esempio
e
Serie Storiche e Processi Stocastici – Federico Andreis
Siano e due v.c. Normali, indipendenti, di media zero e varianze, rispettivamente,
2
. Definiamo il processo stocastico
X costsin t,
t 1,2,...
t
In cui 0 2
è un numero reale fissato. Trattandosi di una combinazione lineare di due v.c.
Normali e indipendenti, il processo X t è ben definito e si potrebbe calcolarne la generale
funzione di densità multivariata. Calcoliamone però i primi momenti che, dalla definizione del
processo, risulteranno funzione dei momenti di e .
Ricordiamo che, per ipotesi, vale
E( ) E(
) 0 ;
Cov( , ) E(
, ) 0
Avremo quindi per il processo che
Var( )
2
;
2
Var( )
E( X ) cos tE( ) sin tE(
) 0 t
t
2 2 2 2
Var( X t ) cos t sin t t
Cov( X , X ) E[( cos t sin t)( cos ( t h) sin (
t h))]
t th 2 2
cost cos ( t h) E( ) sint sin (
t h) E(
)
cos t cos ( t h) sin t sin ( t h)
2 2
Come si vede il valor medio è nullo e quindi costante ma varianza e autocovarianza variano
al variare di t, pertanto, in generale, il processo X t è non stazionario.
2
Se tuttavia supponessimo che Var( ) Var( ) allora le espressioni precedenti
diventerebbero
2 2 2 2
Var( X t ) (cos t sin t) t
Cov X X t t h t t h
2
( t, th ) [cos cos ( ) sin sin (
)]
2 2
cos[ ( )] cos
t k t h t
In definitiva, se Var( ) Var( ) il nostro processo risulta essere stazionario, dal momento
che valgono la condizione 1. di costanza della media, la 2. di costanza e finitezza della varianza
quale che sia t ed infine la 3., ovvero l‟autocovarianza tra t e t h dipende solamente dal lag e
non dall‟istante temporale t.
Sempre sotto le ipotesi suddette la funzione di autocorrelazione del processo risulterà essere
definita da
2

2
h cos
h
2
cos
0 2
Serie Storiche e Processi Stocastici – Federico Andreis
h
cos h,
h0,1,2,3,...
h
h
La funzione è esattamente periodica e risulta evidente come non sia funzione di t ma solo
del lag h.
A conferma della proprietà 5. riguardante la matrice di Toeplitz si osservi che
P
P
(1)
2 2
(2) 1 cos sin 0
P
(3)
10 1 cos
cos 1
1 cos cos2
2
cos 1 cos (1 cos2 )(1 cos2 2cos ) 0
cos2 cos 1
1
cos20
2
1 cos2 2cos 0
2
Dal momento che cos2 2cos 1 l‟ultimo sistema è verificato per ogni appartenente
all‟insieme di definizione che abbiamo fornito, ovvero 0 2
.
Stima della Funzione di Autocorrelazione e Concetto di Ergodicità
Dal momento che la funzione di autocorrelazione h è una misura della struttura interna del
processo stazionario X t assume particolare importanza la sua stima statistica a partire da una
realizzazione finita, ovvero la nostra serie storica { xt , t 1,2,..., N}
. Una considerazione va fatta
prima di considerare i metodi di stima: i dati di cui disponiamo costituiscono una informazione
congiunta sulle v.c. ( X1, X 2,...,
X N ) e non sulla generica X t che definisce, al variare di t, il
processo. La serie storica è quindi una successione ordinata di N campioni di dimensione
unitaria su N distinte v.c. le quali, generalmente, fra loro non sono indipendenti né somiglianti.
La complicazione di stima dei parametri di un processo si presenta quindi già nello studio dei
primi momenti; si immagini cosa può succedere passando a intere funzioni dei parametri (quali
ad esempio, appunto, l‟autocorrelazione). Le procedure classiche di stima da un campione non
sono quindi generalmente utilizzabili, ma risulta d‟altra parte intuitivo supporre che, una volta
verificata la stazionarietà del processo in esame, sia ragionevole aspettarsi che si possa
pervenire ad utili informazioni sui parametri delle v.c. componenti il processo tramite le
informazioni contenute nella serie storica, e questo in virtù della “omogeneità temporale” che
identifichiamo con la stazionarietà, che garantisce una certa qual “stabilità” nei legami
temporali fra le variabili.
L‟esigenza di poter giungere a risultati utili disponendo di un insieme limitato di
informazioni (la nostra serie storica) ha portato alla definizione dell‟importantissimo concetto di
ergodicità, termine originario delle scienze fisiche che nello studio dei processi stocastici
assume il seguente significato:

Serie Storiche e Processi Stocastici – Federico Andreis
Definizione: Un processo stocastico X t è ergodico rispetto ad un parametro se la stima
temporale del parametro, ottenuta da una serie storica, converge in media
quadratica a quel parametro.
Formalmente, dato ˆ( X T ) T 1,2,..., N stimatore del vero parametro e funzione dei dati della
serie storica, diremo che la condizione di ergodicità è verificata qualora
ˆ
2
lim E[ ( XT)
] 0
T
Cos‟è dunque l‟ergodicità? Può essere intesa come una condizione che limita la memoria del
processo: un processo non ergodico è tale da avere caratteristiche di persistenza così accentuate
da far sì che un segmento del processo (nel nostro caso la serie storica) per quanto lungo, sia
insufficiente a dire alcunché sulle sue caratteristiche distributive. In un processo ergodico, al
contrario, la memoria del processo può essere intesa debole su lunghi orizzonti e all‟aumentare
dell‟ampiezza del campione aumenta in modo significativo anche l‟informazione in nostro
possesso. La considerazione che possiamo fare è quella di reputare virtualmente indipendenti
eventi distanti tra di loro sull‟asse temporale in caso di ergodicità: sotto una simile ipotesi
possiamo supporre possibile l‟osservazione di una parte consistente delle traiettorie che il
processo può generare posta una evidenza campionaria sufficientemente grande. Formalmente
la considerazione enunciata poco fa sull‟incorrelazione di eventi distanti nel tempo si traduce
nella seguente condizione necessaria e sufficiente affinché il processo sia ergodico rispetto al
valor medio è che la sua funzione di autocorrelazione tenda a zero al crescere del lag h.
Esiste inoltre un teorema (detto appunto ergodico) che garantisce che se un processo è ergodico
l‟osservazione di una sua realizzazione “abbastanza” lunga è equivalente, per i fini inferenziali,
all‟osservazione di un grande numero di osservazioni.
In linea generale possiamo dire che solo per processi ergodici e stazionari (nota: la
stazionarietà non implica l‟ergodicità! ne è una prova l‟esempio di prima, in cui il processo era
sì stazionario, ma la sua funzione di autocorrelazione era periodica e non tendeva a zero al
divergere del lag) può porsi correttamente il problema dell‟inferenza statistica sulle serie
storiche. L‟ergodicità garantisce che dall‟unica informazione disponibile, appunto le
osservazioni che compongono la nostra serie storica, sarà possibile risalire a stime consistenti in
senso statistico del processo stazionario X t .
D‟ora in avanti supporremo che i processi con cui lavoreremo siano stazionari ed erodici
fino almeno ai momenti del secondo ordine, di modo da dare un senso all‟approccio
inferenziale.
Passiamo dunque alla stima vera a propria della funzione di autocorrelazione h h 0 . Si
tratta semplicemente di trovare uno stimatore soddisfacente per , 0,1,2,... e di lì ricavare
. Premettiamo che per stimare il valor medio del processo EX ( ) impiegheremo la
h
media campionaria
N
t
t1
asintoticamente normale. Si noti però che la varianza di tale stimatore, che solitamente vale
2
N , viene ad essere alterata da un fattore moltiplicativo a causa della correlazione esistente
h h
x X N , il quale, come è noto, è non distorno, consistente ed
fra le X t .
Per comodità di notazione considereremo il processo scarto Zt Xt , il quale possiede
media nulla e la stessa varianza, autocovarianza e autocorrelazione di X t ( trattandosi di una
t

Serie Storiche e Processi Stocastici – Federico Andreis
semplice traslazione). In letteratura sono stati proposti diversi stimatori dell‟autocovarianza, fra
i quali citiamo
ˆ
ˆ
ˆ
1
N
(1)
h ZZ t th N t1
1
Nh (2)
h ZZ t th N h t1
1
Nh (3)
h ZZ t th N t1
Lo stimatore per l‟autocorrelazione sarà in ogni caso
ˆ ih , i 1,2,3
ˆ
i h
i
0
(1) ˆ h è dotato di notevoli proprietà teoriche, ma implica una condizione molto
Lo stimatore
restrittiva per il suo utilizzo, ovvero il processo deve ripetersi esattamente dopo N unità
temporali, cioè deve essere del tipo ZN 1 Z1, ZN 2 Z2,..., ZN i
Zi,...
.
Per quanto riguarda gli altri due stimatori si osservi che per N elevato rispetto a k vale
(3) (2) ˆ ˆ , dunque la differenza risulta evidente solo nei piccoli campioni. E‟ stato dimostrato
h h
inoltre che
(2) ˆ h è stimatore corretto per h ma
(3) ˆ h , pur essendo distorto, garantisce un errore
(2) ˆ h , risultando dunque più efficiente e, soprattutto,
quadratico medio inferiore a quello di
verifica la condizione per la quale P ˆ
( m)
, ovvero la matrice di Toeplitz stimata, è definita
positiva, proprio come P ( m)
; questo non avviene necessariamente costruendo P ˆ
( m)
con lo
(2) ˆ h . Per questi motivi di norma la preferenza cade su
stimatore
funzione di autocorrelazione nel modo seguente:
N hNh
Z Z ( X x)( X x)
ˆ
ˆ , h 0,1,2,...
(3)
t thtth h t1 t1
h (3) ˆ 0
N
2
Zt N
(
X t
2
x)
t1 t1
(3) ˆ h e dunque si stima la
Lo stimatore è simmetrico ( ˆ ˆ h h) e pertanto la stima viene effettuata solo per h positivo.
In pratica come si procede? Nota la serie storica ( x1, x2,..., x N ) si costruisce la serie degli
scarti z1 x1 x, calcola
z2 x2 x, ..., zN xN x (dove x è la usuale media campionaria) quindi si
Nh 1
ˆ z z , h 0,1,2,...
h t th N t1

Serie Storiche e Processi Stocastici – Federico Andreis
fino ad un lag massimo che l‟esperienza pone pari a N 4 o al suo intero successivo. Fatto
questo si costruiscono i rapporti ˆ ˆ ˆ
h h 0 per h 0,1,2,..., N 4 e si riportano su di un grafico
denominato correlogramma, solitamente a barre verticali per ciascun h per sottolineare che si
tratta di stime in punti discreti; talvolta si uniscono i punti della funzione di autocorrelazione per
evidenziarne l‟andamento complessivo.
Esempio
Sia xt (8.5, 10.3, 9.6, 8.7, 11.2, 9.9, 7.9, 10.9, 11.1, 10.4) la nostra serie storica il cui
grafico è illustrato di qui di seguito
e la quale media campionaria vale x 9.79 (tratteggiata nel grafico). La serie degli scarti è
z ( 1.35, 0.45, 0.25, 1.15, 1.35, 0.05, -1.95, 1.05, 1.25, 0.55) . Dal momento che
t
N=10 N4 2.5 dunque avrà senso calcolare ˆ h solo per h 0,1,2,3 . Dunque
1 1
ˆ 0
N
N
10
2 2
zi zi
i1 10 t1
1 1.82250.20250.06251.32251.8225
10 0.0025 3.8025 1.1025 1.5625 0.3025
1
12.005 1.2
10
N 1
9
1 1
ˆ z z z z
1 t t1tt1 N i1 10 t1
1 0.60750.11250.28751.55250.0675
10 0.0975 2.0475 1.3125 0.6875
1
2.0625 0.21
10

N 2
8
1 1
ˆ z z z z
2 t t2tt2 N i1 10 t1
Serie Storiche e Processi Stocastici – Federico Andreis
1 0.33750.51750.33750.0575
10 2.6325 0.0525 2.4375 0.5775
1
5.015 0.5
10
N 3
7
1 1
ˆ z z z z
3 t t3 t 3
N i1 10 t1
1 1.55250.60750.01252.2425
10 1.4175 0.0625 1.0725
1
4.7975 0.48
10
Dunque le stime della funzione di autocorrelazione saranno:
ˆ ˆ ˆ 1
0 0 0
ˆ ˆ ˆ 0.21 1.2 0.18
1 1 0
ˆ ˆ ˆ 0.5 1.2 0.42
2 2 0
ˆ ˆ ˆ 0.48 1.2 0.40
3 3 0
Il correlogramma sarà quindi, per i lags h 0,1,2,3 , il seguente:
Le linee tratteggiate delimitano la regione di confidenza approssimata per l‟ipotesi
0 : H Xt WN e si ottengono da 2 N 2 10 0.6325 . In ambiente R, ovvero il software
impiegato per tracciare questi grafici, tale precisazione viene eseguita in automatico nel
momento del calcolo della funzione di autocorrelazione; le bande così ampie, che porterebbero a
non poter rifiutare l‟ipotesi di cui sopra, sono dovute ad un N così piccolo.

Serie Storiche e Processi Stocastici – Federico Andreis
Passiamo ora a parlare di un altro importantissimo strumento dell‟analisi dei processi
stazionari, ovvero la funzione di autocorrelazione parziale, il cui ruolo fondamentale risulterà
più chiaro nel seguito, quando tratteremo dei cosiddetti modelli autoregressivi.
Definiamo quindi la funzione di autocorrelazione parziale h al lag h, per h 0, 1, 2,... ,
come la correlazione esistente fra t X e X t h al netto della correlazione esistente fra le v.c.
“intermedie” tra t X e X t h.
Se la definizione può risultare di non semplicissima comprensione, la forma analitica della
funzione è estremamente semplice: la funzione di autocorrelazione parziale è data dal rapporto
fra due determinanti
Con
P
( h)
P
*
( h)
*
P(
h)
h , h 0,1,2,...
P
( h)
1 1 2 ... h1
1 ...
1 1 h2
2 1 1 ... h3
;
. . . ... .
. . . ... .
... 1
h1 h2 h3
1 1 2 ... 1
1 ...
1 1 2
2 1 1 ... 3
. . . ... .
. . . ... .
...
h1 h2 h3 h
Dove P ( h)
è la matrice di Toeplitz di ordine h, mentre
P è la stessa matrice alla cui ultima
colonna è stato sostituito il vettore composto dai valori della funzione di autocorrelazione fino al
lag h. Dalla proprietà di simmetria di h discende anche quella di h , difatti vale h h,
quindi anche in questo caso i calcoli verranno effettuati esclusivamente per valori positivi di h.
E‟ ovviamente vero che 0 1 , mentre applicando la definizione per h 1,2,3 otteniamo:
1
1 1
1
1
1
2
1
1
2
1
2
2 1
2
1
1
1
1
*
( h)

1
1 1
1
1 2
Serie Storiche e Processi Stocastici – Federico Andreis
1 2 2
2
2
2 1 3 3 1 1 1 2 2
3
2 2
1 1 2 1 1 1 2 21
1
1 1
2 1
1
Risultano inoltre univocamente determinabili i valori della funzione di autocorrelazione in
funzione delle autocorrelazioni parziali fino allo stesso lag h:
1 1
1
2 2
2
1 2
2 2 3
2
1 1 1 2
3 3 2 1 1 2 1 2 2
E‟ possibile (per quanto non immediato) ricavare una forma analitica generale in modo da
esplicitare h in funzione di h, h
1,..., 1
e viceversa; tale problema è sempre risolubile, per
quanto non molto semplice.
Come si può vedere dalla teoria esposta sino a qui h e h sono l‟una funzione dell‟altra:
h non aggiunge nulla sulla conoscenza del processo che non sia già teoricamente deducibile da
h ; come già accennato l‟importanza della funzione di autocorrelazione parziale risulterà
evidente più avanti, nell‟ambito della stima dei modelli autoregressivi.
Per quanto riguarda la stima della funzione di autocorrelazione parziale il metodo più
immediato consiste nel ricavare le stime di h , ad esempio tramite lo stimatore introdotto
prima, ed andarle a sostituire all‟interno delle matrici definite sopra, di modo da ottenere
*
Pˆ
( h)
ˆ h , h 0,1,2,...
Pˆ
( h)
ˆ *
P ( h)
e P ˆ
( h)
sono, rispettivamente, la matrice di Toeplitz e la stessa modificata di cui già si è
parlato, nelle quali sono stati inseriti i valori stimati della funzione di autocorrelazione.
Analogamente al caso della funzione di autocorrelazione si rappresenta graficamente anche
ˆ h per lo stesso numero di lags per cui è stata stimata h . Tale grafico viene denominato
talvolta come correlogramma parziale.
Esempio
Riprendiamo i dati derivati dalla serie storica dell‟esempio precedente, per la quale avevamo
già stimato i valori della funzione di autocorrelazione fino al lag h 3.

1 1 0
2 2 0
3 3 0
Serie Storiche e Processi Stocastici – Federico Andreis
ˆ ˆ ˆ 0.21 1.2 0.18
ˆ ˆ ˆ 0.5 1.2 0.42
ˆ ˆ ˆ 0.48 1.2 0.40
Procedendo con i calcoli e sfruttando i risultati presentati in precedenza otteniamo le stime
dell‟autocorrelazione parziale:
ˆ 1
ˆ ˆ
1 1
0.18
1
1 ˆ 1
ˆ
ˆ
ˆ ˆ 0.42 ( 0.18)
0.468
2 2
1 2 2 1
2
1 ˆ 1 2
1 ˆ 1
2
1 ( 0.18)
ˆ 1
1
1 ˆ 1 ˆ 1
ˆ 1 1 ˆ 2
ˆ
ˆ
ˆ ˆ
ˆ ˆ ˆ ˆ ˆ
1 2 2
2
2
1 1 2
2 1 3 3 1 1 1 2 2
3
1 ˆ 1 ˆ 2 2 ˆ 1 ˆ 2 2 ˆ 1
ˆ 1 1 ˆ 1
ˆ ˆ 1
2 1
2
2
2
2 2
1 ( 0.18) 1 ( 0.42) 2( 0.18)
0.40 1 ( 0.18) 0.18 ( 0.18) ( 0.42) 2( 0.42)
0.398
Come si può notare le stime delle due funzioni sono praticamente coincidenti, a meno di
approssimazioni minime. Nel grafico che segue è riportato il correlogramma parziale del
processo sulla base della serie storica data.

Serie Storiche e Processi Stocastici – Federico Andreis
Anche in questo caso sono presenti i limiti approssimati della regione di confidenza al 95%
H X WN . La costruzione è analoga a quella relativa alla funzione di
per l‟ipotesi 0 : t
autocorrelazione, le bande di confidenza sono poste a 2 N 2 10 0.6325 intorno allo
zero; chiaramente nel nostro caso tale specificazione è superflua, dal momento che la serie
storica che è stata impiegata per l‟esercizio è artificiale.
La Classe dei Modelli ARMA
Come si è già visto in precedenza lo scopo dell‟analisi delle serie storiche è quella di risalire
ai processi stocastici che si suppone le abbiano generate; operativamente questo si traduce
nell‟identificazione e nella stima di modelli statistici che garantiscano un accettabile grado di
approssimazione della realtà in esame. Dunque dai dati non si perviene al processo bensì se ne
costruisce una descrizione valida sino a prova contraria: una sintesi cioè ottimale solo fino a che
nuovi dati non porteranno a costruire modelli più convincenti. In generale la conoscenza di un
processo a partire dai dati è proibitiva, dunque si ripiega su di un particolare modello: il
processo stocastico genera la serie storica quale sua realizzazione finita, il modello statistico si
adegua alla serie storica secondo criteri di ottimalità e genera dati che sono simulazioni ottenute
dal modello. Nel seguito presenteremo una classe di modelli statistici che trova il suo impiego
nella descrizione dei processi stocastici, i modelli ARMA. Il passo seguente all‟identificazione è
chiaramente costituito dalla validazione del modello scelto tramite opportune verifiche di
ipotesi; una volta assicurata la bontà del modello si può infine passare alla previsione.
Il Processo a Media Mobile
Sia A t un processo white noise come già definito in precedenza e si consideri il seguente
processo stocastico
Yt At At dove , . Questa serie storica è definita processo a media mobile del primo ordine, e si
indica con MA (1) . Il termine “media mobile” deriva dal fatto che Y t è costruito da una somma
pesata, simile ad una media, dei due più recenti valori di A .
Il valore atteso di Y t è dato da
E Y E A A E A E A
t t t1 t t1
dal momento che abbiamo definito A t come un white noise, e quindi a media nulla per ogni t.
La varianza di Y t , che coincide chiaramente con la funzione autocovarianza calcolata per un
lag nullo, vale
2 2 2 2 2
t t t1 t 2
t t1 t1
E Y E A A E A A A A
2 2 2
0
1
2 2
0
1

La prima autocovarianza è
Serie Storiche e Processi Stocastici – Federico Andreis
E Y Y E A A A A
t t1 t t1 t1 t2
2 2 2
t t1 t1 t t2 t1 t2
E A A A A A A A
0 0 0
2 2
1
Le autocovarianze di ordine superiore sono tutte identicamente nulle.
Dal momento che la media e le autocovarianze non sono funzioni del tempo t, un processo
MA (1) à stazionario quale che sia il valore di . Inoltre è chiaramente soddisfatta la seguente
condizione di ergodicità rispetto alla media
h
,
difatti h
2 2 2
1
h0
h0
supponendo finito (ed è una assunzione quasi scontata, altrimenti non avrebbe senso la
2
costruzione di un modello) e sapendo che è finito poiché stiamo considerando un disturbo di
tipo white noise (analogo è il discorso sulla condizione di asintoticità verso lo zero: dal
momento che h 0, h 1 è verificata anche quest‟ultima). Inoltre se supponiamo che il
processo di rumore bianco sia anche gaussiano, allora l‟ergodicità è valida con rispetto a tutti i
momenti.
La funzione di autocorrelazione è pari all‟unità per h 0 , mentre per h 1 vale
2
1
1
2 2
2
0 1
1
le autocorrelazioni di ordine superiore sono tutte identicamente nulle ed è possibile
rappresentare h in un correlogramma.
E‟ interessante notare come esistano sempre due distinti valori di tali da restituire il
medesimo valore della funzione di autocorrelazione. Difatti se andiamo a sostituire a il valore
1 notiamo che
2
11
11 11 1
1 2
2
2
2
Per esempio, i processsi Yt autocorrelazione data da
At 0.5At
1
e Yt At 2At
1
hanno la medesima funzione di
2 0.5
1 0.4
2 2
1210.5

Il grafico di 1
2
1
è il seguente:
Serie Storiche e Processi Stocastici – Federico Andreis
Sono stati simulati quattro processi a media mobile del primo ordine sotto ipotesi di media
nulla e con rumore bianco gaussiano (la stazionarietà non è richiesta in quanto sempre
verificata); di seguito le rappresentazioni grafiche delle serie storiche per un totale di 300
realizzazioni, con i rispettivi correlogrammi (ACF) e correlogrammi parziali (Partial ACF).
Le funzioni di autocorrelazione (ACF) mostrano come, dopo il primo lag, i valori possano
ritenersi ragionevolmente nulli (dal momento che non superano le bande di confidenza; è
accettabile inoltre un valore “anomalo” ogni 20 lag, purché superi in modo non significativo i
valori limite). Questo significa che abbiamo a che fare con modelli a media mobile di ordine 1
(come in effetti sono per costruzione); la vera utilità di questo genere di considerazioni grafiche
risiede nel fatto che nella cosiddetta fase di identificazione dei modelli possiamo essere in
grado, semplicemente costruendo i correlogrammi campionari dalla nostra serie storica, di
orientarci verso un tipo di modello o verso un altro a seconda della “forma” della funzione di
autocorrelazione .
Le funzioni di autocorrelazione parziale (Partial ACF), invece, mostrano un andamento
decrescente e convergente verso lo zero: questo è tipico dei modelli a media mobile.

Serie Storiche e Processi Stocastici – Federico Andreis

Serie Storiche e Processi Stocastici – Federico Andreis

Serie Storiche e Processi Stocastici – Federico Andreis
Definiamo ora il processo a media mobile di ordine q, che indicheremo con MA( q ) , nel
seguente modo:
Y A A A A
t t 1 t1 2 t2 ... q
tq Ovvero estendiamo ad un numero di q termini la somma pesata dei white noise che riteniamo
descrivano la nostra Y t . In pratica viene aumentato il peso delle informazioni fornite dai disturbi
più lontani nel tempo, fino ad un lag, appunto, pari a q. MA (1) è chiaramente un caso
particolare di processo a media mobile di ordine q nel quale i pesi j risultino pari a zero per
j 1.
Calcoliamo il valore atteso del processo
La varianza sarà
t t 1 t1 2 t2 ... q
tq
E At 1EAt1... qE At
q
E Y E A A A A
2
2
0 E Yt E At 1At 1 2At 2 ... q At
q
dal momento che, per ipotesi, i rumori bianchi sono incorrelati tra di loro la varianza della
somma sarà semplicemente pari alla somma delle varianze, ovvero
... 1 ...
2 2 2 2 2 2 2 2 2 2 2
0 1 2 q 1 2
q
Si ricava inoltre (non lo dimostriamo ma è semplice ottenerlo) che
2
h h h q qh 1 1 2 2 ... h1,2,..., q
h
0
hq Per esempio in un processo MA (3) avremo che:
1
2 2 2 2
0 1 2 3
2
2
2
1 1 2 1 3 2
2 2 3 1
3 3
... 0
4 5
La funzione di autocorrelazione segue automaticamente rapportando i valori di h alla
varianza, ed è identicamente nulla per h q,
dunque anche il processo MA( q ) risulta essere
stazionario, quali che siano i valori dei parametri j ; inoltre, come già per il processo di ordine

Serie Storiche e Processi Stocastici – Federico Andreis
1, se il disturbo è di tipo white noise gaussiano è rispettata anche l‟ergodicità rispetto a tutti i
momenti.
Di seguito quattro esempi di processo (2)
MA ; le considerazioni sono le medesime già fatte
per il caso del modello a media mobile di primo ordine e ancora una volta supponiamo valor
medio nullo e disturbi di tipo white noise gaussiano.

Serie Storiche e Processi Stocastici – Federico Andreis

Il processo MA( q ) può essere scritto come
Si consideri cosa succede quando q :
Serie Storiche e Processi Stocastici – Federico Andreis
Y A , 1
t j t j
j0
q
Y A A A A ...
t j t j 0 t 1 t1 2 t2
j0
Questo può essere considerato un processo MA( ) , che risulta essere stazionario se è verificata
la seguente condizione:
j0
2
j
Spesso si considera la condizione leggermente più restrittiva
Una sequenza di coefficienti j
j
0
j0
j
0
che rispetti le condizioni sopraelencate viene definita,
rispettivamente, di quadrato sommabile e assolutamente sommabile. Questo garantisce anche
che sia rispettata la condizione di ergodicità rispetto alla media (
h0
h
),
in effetti anche le
covarianze sono assolutamente sommabili. Il valor medio del processo MA( ) rimane
comunque , mentre i momenti di ordine superiore basta far tendere ad infinito l‟ordine q nelle
espressioni già ricavate e calcolare il limite.
Il Processo Autoregressivo
Un processo autoregressivo del primo ordine, indicato con AR (1) , soddisfa la seguente
equazione:
Y c Y A
t t1 t
Ancora una volta A t è il rumore bianco che soddisfa tutte le proprietà già discusse e c, .
Come si può vedere si tratta di una equazione alle differenze finite di ordine 1, ed è noto
dalla teoria che se 1 la conseguenza degli t A sulla Y t tenderanno ad accumularsi nel tempo
piuttosto che tendere a zero. Dovrebbe risultare dunque sufficientemente intuitivo comprendere
la seguente affermazione: qualora 1,
allora non esiste un processo stazionario Y t che
soddisfi l’equazione Yt Yt1 At
.
In caso invece sia 1,
allora esiste un processo stazionario Y t che soddisfi l‟equazione e
che sarà dato dalla soluzione stabile

Serie Storiche e Processi Stocastici – Federico Andreis
1 2
2 3
3
c1
A A
2
A
3
A ...
Y c A c A c A c A ...
t t t t t
tt1
t2 t3
j
Tale soluzione può essere vista come un processo MA( ) con . Qualora la condizione
1 sia soddisfatta, allora avremo
j 1
1
j
j0 j0
La convergenza di questa serie garantisce l‟esistenza della rappresentazione MA( ) e
l‟ergodicità rispetto alla media del processo AR (1) .
Calcolando il valore atteso della soluzione otteniamo che
Dunque la media di un processo (1)
La varianza invece è
mentre la h-esima autocovarianza vale
E Yt c1 0 0 ...
AR stazionario vale c 1
.
t
2
t t1 2
t2 3
t3
...
2 4 6 2
1 ...
2
2 1 0
E Y E A A A A
t th t t1 2
t2 ...
h
th h1 th 1 h2
th 2
...
2
At h Ath1 At
h2 ...
E Y Y E A A A A A A
h h2h4 2
...
h 2 4 2
1 ...
1
h 2 2
h
Segue immediatamente l‟espressione della funzione di autocorrelazione, pari a
0
h 2 2 h 2 2
11 h
h
h
2 2 2 2
11 j
2

Serie Storiche e Processi Stocastici – Federico Andreis
la quale rispetta la condizione di convergenza a 0, sotto ipotesi di stazionarietà, dal momento
che si è supposto 1.
Sono stati simulati quattro processi autoregressivi del primo ordine sotto ipotesi di
stazionarietà, media nulla e con rumore bianco gaussiano; di seguito le rappresentazioni
grafiche delle serie storiche per un totale di 300 realizzazioni, con i rispettivi correlogrammi
(ACF) e correlogrammi parziali (Partial ACF).
Si noti come le funzioni di autocorrelazione decrescono progressivamente e lentamente
verso lo zero (l‟alternanza dei segni dipende unicamente dal segno del parametro ), questa è
una caratteristica tipica dei processi di tipo AR ; le funzioni di autocorrelazione parziale invece
presentano un solo valore significativamente al di fuori delle bande di confidenza, il primo,
questo ci fornisce l‟indicazione che si tratti di processi del primo ordine. Nelle Partial ACF i
valori successivi al primo non sono nulli come vorrebbe la teoria, ma questo è imputabile al
caso, possiamo accettare l‟ipotesi di in correlazione temporale per lag superiori a 1 dal
momento che, appunto, i valori della funzione non superano le bande di confidenza (è
accettabile inoltre un valore “anomalo” ogni 20 lag, purché superi in modo non significativo i
valori limite)

Serie Storiche e Processi Stocastici – Federico Andreis

Serie Storiche e Processi Stocastici – Federico Andreis
Cosa succede però se la condizione di stazionarietà non è rispettata (ovvero se il parametro è
tale che 1)?
Il processo esplode. Nel grafico che segue sono state rappresentate le
simulazioni di due processi autoregressivi con parametri superiori in modulo a 1, seppure di
pochissimo.

Serie Storiche e Processi Stocastici – Federico Andreis
Chiaramente la stazionarietà non è più rispettata, e sebbene le funzioni di autocorrelazione
ed autocorrelazione parziale conservino un andamento che potremmo definire “ideale”, risulta
evidente come l‟esplosione dei valori renda il modello assolutamente instabile.
Analogamente al caso del processo a media mobile, possiamo estendere il concetto di
autoregressione ad ordini superiori; rendiamo, cioè, significative informazioni sul processo più
lontane nel tempo, fornendo loro pesi non nulli.
Si definisce processo autoregressivo di ordine p e si indica con AR( p ) il seguente:
Y c Y Y Y A
t 1 t1 2 t2 ... p t p t
Ovvero estendiamo ad un numero di p termini la somma pesata dei valori passati della nostra Y t ,
con l‟aggiunta di un termine di disturbo white noise A t . Risulta evidente come il processo
AR (1) presentato in precedenza altro non sia che un caso particolare di quest‟ultimo, con 0
per 1
j .
A differenza del processo a media mobile, come si è già detto, la stazionarietà non è
necessariamente rispettata; dobbiamo dunque imporre delle condizioni sui parametri del
j

Serie Storiche e Processi Stocastici – Federico Andreis
modello. In particolare richiederemo che i coefficienti j associati alle radici dell‟equazione
omogenea associata
2
p
1 12... p
0
siano tali da garantire che 1 j . In questo caso il processo non esplode e si mantiene
j
stazionario.
Nel caso di un processo AR (2) questa condizione è graficamente rappresentabile in modo
comprensibile; si tratta infatti della condizione che i due parametri 1 e 2 si trovino all‟interno
del triangolo tratteggiato nella figura sottostantante.
Sotto l‟ipotesi di stazionarietà il valore atteso del processo è:
c
EY
t 1 ...
1 2
e sfruttando questa espressione l‟equazione che descrive il processo può essere riscritta nel
modo seguente:
Y Y Y Y A
t 1 t 1 2 t 2 ... p t p t
Le autocovarianze si possono quindi ottenere semplicemente moltiplicando ambo i membri
Y e prendendone i valori attesi; ne risulta che:
dell‟ultima equazione per
th 1 h1 2 h2 ... p h p h 1,2,...
h
2
1 1 2 2 ... pp h 0
p
) questo
Sfruttando la nota proprietà di simmetria della funzione di autocovarianza ( h h
sistema di equazioni può essere risolto per
2
0, 1,..., p in funzione di , 1, 2,..., p . Per
ricavare la funzione di autocorrelazione basterà dividere per 0 , quindi:

chiaramente 0 1 .
Serie Storiche e Processi Stocastici – Federico Andreis
h 1 h1 2 h2 ... p h p
L‟espressione precedente, esplicitata per h 1,2,... , dà origine al cosiddetto sistema di
equazioni di Yule-Walker, che costituisce lo strumento fondamentale per la stima dei parametri
del modello autoregressivo. Come già detto è possibile, noti che siano i parametri e la varianza
del disturbo, stimare i valori della funzione di autocovarianza (e quindi di autocorrelazione); ciò
che risulta invece di effettivo interesse operativo è proprio l‟operazione inversa, in effetti noi
disponiamo della serie storica dei dati dalla quale, come si è già mostrato negli esempi, si
possono stimare i valori della funzione di autocorrelazione. Tramite il sistema di equazioni di
Yule-Walker abbiamo quindi la possibilità di stimare i parametri (ignoti) del modello
autoregressivo che meglio approssimi il processo stocastico (a tutti gli effetti inconoscibile nella
sua completezza) di cui la serie storica rappresenta una realizzazione finita.
Il sistema di equazioni di Yule-Walker si presenta in forma lineare per il processo
autoregressivo, e può essere esplicitato come segue:
1 1 2 1 3 2 ...
pp1
2 11 2 3 1 ...
pp2
.....
.....
p 1 p1 2 p2 3 p3 ...
p
Dunque potremo sostituire ai valori j le loro stime ˆ j ottenute dalla serie storica, ed
ottenere quindi le stime ˆ j dei parametri del modello. Si noti inoltri che la soluzione è unica, dal
momento che la matrice del sistema altro non è che la matrice di Toeplitz di ordine p, P ( p)
, la
quale è definita positiva per ogni p quando il processo è stazionario.
L‟approccio di Yule-Walker per la stima dei parametri è applicabile anche ai processi a
media mobile, si ricava però un sistema non lineare di equazioni, che richiede una procedura di
calcolo iterativa particolare. Risulta così più laborioso determinare le stime ˆ j, j 1,2,..., q in
base a stime delle autocorrelazioni ˆ j, j 1,2,..., q determinate dall‟evidenza campionaria (la
nostra serie storica).
Seguono alcuni esempi di processi autoregressivi del secondo ordine; le considerazioni sono
esattamente le stesse già presentate per quelli del primo ordine (stazionarietà, media nulla,
disturbo white noise gaussiano). Le quattro simulazioni sono state effettuate con alternanza di
segni dei parametri 1, 2 per rendere evidenti le differenti forme delle funzioni di
autocorrelazione.

Serie Storiche e Processi Stocastici – Federico Andreis

Serie Storiche e Processi Stocastici – Federico Andreis
Abbiamo presentato in precedenza la condizione affinché un processo autoregressivo del
, si trovi all‟interno del
secondo ordine sia stazionario, ovvero che il punto di coordinate 1 2
triangolo tratteggiato in figura. Analogamente al caso dei processi di tipo AR 1 anche quelli di
ordine superiore esplodono qualora non siano rispettate le condizioni sui parametri, ne vediamo
di seguito qualche esempio grafico:

Serie Storiche e Processi Stocastici – Federico Andreis

Serie Storiche e Processi Stocastici – Federico Andreis
Volendo riassumere brevemente quanto detto finora possiamo sottolineare il carattere di
dualità tra i processi AR e MA .
I processi di tipo AR rispondono al tentativo di spiegare il presente in funzione del
passato, fino ad una certa “distanza” p, per contro i modelli di tipo MA rappresentano un
tentativo di spiegare il presente come risultante da una successione incontrollata di
impulsi casuali, statisticamente riassunti nel white noise A t .
In un processo AR( p ) non sono imposte condizioni per i parametri in modo da
assicurare l‟invertibilità, mentre si richiedono per la stazionarietà.
In un processo MAq non sono imposte condizioni sui parametri per quanto riguarda la
stazionarietà, mentre le si impongono per l‟invertibilità.
Per ogni processo AR( p ) stazionario esiste una rappresentazione unica del tipo
MA , e per ogni processo MAq invertibile ne esiste una del tipo AR .
Nei processi MAq teorici il correlogramma si annulla bruscamente per h q,
il
correlogramma parziale invece decresce lentamente con andamento dipendente dal
segno dei parametri j .
Nei processi AR( p ) teorici il correlogramma parziale si annulla bruscamente per h q
mentre il correlogramma decresce lentamente con andamento dipendente dal segno dei
parametri j .
All‟atto pratico si considerano come nulle, al fine dell‟identificazione del modello a
partire dai dati, quelle autocorrelazioni che restino comprese fra le due bande tratteggiate
nei correlogrammi, con un livello di confidenza del 95%.
I Modelli Autoregressivi a Media Mobile
Un modello del tipo autoregressivo a media mobile di ordini p e q, indicato con
ARMA( p, q ) , è un costrutto statistico che comprende sia termini autoregressivi che a media
mobile e può essere espresso come segue:
Y c Y Y ... Y A A A ... A
t 1 t1 2 t2 p t p t 1 t1 2 t2 q tq Per comodità di rappresentazione introduciamo ora l‟operatore retrocessore o backward B
secondo la seguente definizione:
0
B X t Yt
BX Y
t t1
2
B X t Yt2
...
k
B X t Yt
k
Trattandosi di un operatore lineare vale la seguente:
0 1B Xt 0X t 1X t1
.
Se consideriamo il processo MA( q ) Y t con media supposta nulla possiamo scriverlo
sfruttando l‟operatore B come

Serie Storiche e Processi Stocastici – Federico Andreis
Y A A A ...
A
t t 1 t1 2 t2 q tq Y A BA B A ...
B A
2
q
t t 1 t 2 t q t
Y
B
A
Y B A
q
t 1j j1
j
t
t t
mentre un processo AR( p ) Y t con termine c pari a zero può essere rappresentato come
Y Y Y ... Y A
t 1 t1 2 t2 p t p t
Y BY B Y ... B Y A
2
p
t 1 t 2 t p t t
p
j
1jBYt At
j1
B Y A
t t
Notiamo anche in questa sede la dualità già discussa in precedenza: le funzioni B e
B sono dei filtri lineari che, in questa formulazione, nel caso dei modelli AR( p ) filtrano
l‟informazione passata e restituiscono “l‟innovazione” sotto forma di un rumore bianco, nel
caso dei modelli MA( q ) filtrano i disturbi passati e restituiscono l‟informazione al tempo
presente. L‟utilità di questa rappresentazione risulta evidente qualora ci interessasse ricavare i
parametri del modello di ordine infinito di tipo AR associato al MA di ordine finito (qualora
sia rispettata l‟invertibilità) o viceversa; si noti infatti che le relazioni definite prima permettono
di scrivere:
B Yt
At
B B At At
BB1 B 1BB1B
Seguendo la notazione appena introdotta potremo quindi esprimere il processo di tipo
ARMA( p, q ) come segue:
Y Y Y ... Y c A A A ...
A
t 1 t1 2 t2 p t p t 1 t1 2 t2 q tq
1
1
B Y c B A
p q
j
jBYtc j
jBAt
j1 j1
t t
I modelli ARMA dunque altro non sono che combinazioni dei modelli autoregressivo e a
media mobile. L‟importanza pratica del modello misto risiede nel fatto che per molte serie

Serie Storiche e Processi Stocastici – Federico Andreis
temporali esso richiede un numero di parametri inferiore a quelli necessari per un modello
autoregressivo puro.
ARMA p, q sia stazionario è legata alle radici
La condizione affinché un processo
dell‟equazione caratteristica della parte autoregressiva del modello, che si ottiene uguagliando a
B . Si tratta esattamente delle stesse condizioni imposte per il modello
zero l‟operatore
AR p e già discusse in precedenza, e rileggendole alla luce della nuova formulazione
richiedono che le radici B , j 1,..., p dell‟operatore siano tutte in modulo superiori ad 1 (nel
j
caso AR 2 questa condizione si riflette sui parametri in modo da costringerli all‟interno del
triangolo di cui in precedenza). In questo caso per il processo esiste anche una rappresentazione
del tipo MA .
Analogamente la condizione per l‟invertibilità coincide con quella già presentata relativa al
modello MAq , ovvero è legata alle radici dell‟equazione caratteristica della parte a media
mobile, che si ottiene uguagliando a zero l‟operatore B . Le radici B , j 1,..., q dovranno
essere tutte in modulo superiori ad 1. In questo caso per il processo esiste anche una
rappresentazione del tipo AR .
In sostanza: se il processo ARMA p, q è stazionario ed invertibile lo si può approssimare,
trascurando un certo numero di termini, in un processo AR p o in un MAq .
Risulta inoltre chiaramente che i processi autoregressivo di ordine p e a media mobile di
ARMA p, q , infatti:
ordine q sono casi particolari del più generale
p 0 ARMA p, q MAq
q 0 ARMA p, q AR p
Il valore atteso del processo risulta essere:
t 1 t1ptp E Y c E Y ... E Y 0 0 ... 0
c
EY t
1 ...
1 2
La funzione di autocovarianza è fornita dalle seguenti due relazioni:
dove
h 1 h1 ... p h p h 1 h1 ... q hq hq
h 1 h1 2 h2 ... p h p
hq
h E Yt E Yt At E At
è la covarianza incrociata tra le variabili t Y e A t .
La varianza ha quindi, per le note proprietà di simmetria della covarianza, la seguente
espressione:
... ...
2
0 1 1 p p 1 1
q p
p
j

Serie Storiche e Processi Stocastici – Federico Andreis
si noti che è possibile calcolare la varianza soltanto se sono note 1 ,..., p , che si trovano
risolvendo la funzione di autocovarianza espressa nel sistema precedente.
L‟autocorrelazione risulta immediatamente dalla seconda equazione del sistema e vale
h 1 h1 2 h2 ... p h p h q
La funzione di autocorrelazione può avere andamenti molto diversi, la regola generale è che
i primi q coefficienti sono sostanzialmente arbitrari, dopo di che la ACF converge verso lo zero
come fa, a partire da zero, la funzione di autocorrelazione di un AR p . Dunque la ACF è
composta da un numero infinito di termini, e così anche la funzione di autocorrelazione parziale,
che si comporta nello stesso modo ma invertendo i termini (a q si sostituisce p e ad AR p
MA( q ) . Di seguito i grafici teorici delle funzioni di autocorrelazione e autocorrelazione parziale
per alcuni processi di tipo ARMA p, q .

Serie Storiche e Processi Stocastici – Federico Andreis
E‟ importante notare che, a parte per la „regola generale‟ di prima, non arrestandosi ad un
certo lag queste funzioni non ci forniscono indicazioni sull‟ordine di un eventuale modello
autoregressivo a media mobile da applicare ai dati.
Vediamo ora il caso più semplice ed impiegato di modello misto, l‟ ARMA 1,1 , che è
esprimibile nella forma
Y c YA A
t 1 t1t1t1 La condizione di stazionarietà di un processo ARMA p, q coincide con quella di un
modello del tipo
1.
AR p , dunque il processo è stazionario a condizione che 1

Serie Storiche e Processi Stocastici – Federico Andreis
La condizione di invertibilità è la stessa di un processo MAq , dunque nel nostro caso sarà
verificata qualora 1 1.
Il valor medio risulta essere EY
t
c
, mentre la funzione di autocovarianza vale
1
1
12
0
2
1 0
2
2
1
2
2 1 1
2
0
2
1
2
1
1
1 1 2
2
1 1 0 1
h 1 h1
h1
1 1
L‟autocorrelazione segue immediatamente rapportando h a 0 . In generale (per h 2 )
varrà che h 1h1. In condizioni di stazionarietà questa funzione decresce verso lo zero al
crescere del lag h secondo un andamento smorzato di tipo esponenziale con segni dipendenti dal
segno di 1.
Di seguito si riportano i grafici di quattro simulazioni di processi ARMA 1,1 al variare dei
parametri 1
e 1
. Si mostra anche cosa succede qualora la condizione di stazionarietà non sia
rispettata.

Serie Storiche e Processi Stocastici – Federico Andreis
Se invece non è rispettata la condizione di stazionarietà 1 1 il software si rifiuta di
rappresentare i modelli facendo notare che non sono stazionari, ma per farci un‟idea possiamo
imporre un valore di 1 molto prossimo ad 1, diciamo 0.999: