Le travi: flessione e taglio

Le travi: flessione e taglio
Le travi sono elementi monodimensionali ossia con una dimensione prevalente rispetto alle altre
due e soggetti prevalentemente a forze applicate in direzione perpendicolare al loro asse.
Le azioni interne che si sviluppano nelle travi sono quindi prevalentemente momento flettente e
taglio che generano, rispettivamente, tensioni normali e tensioni tangenziali.
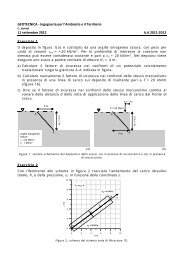
Come appare chiaramente nell’esempio riportato in figura mentre il taglio dipende solo dal valore
della forza, il momento flettente dipende anche dalla luce della trave e quindi, a parità di carico
applicato, travi di luce maggiore sono soggette a momenti flettenti più elevati. Nella figura si vede
che se la luce della trave raddoppia anche il momento in ogni sezione raddoppia. Abbiamo ignorato
il peso proprio ma in genere questo è un’aliquota piccola del carico agente.
P
A B C
l / 2
l /
2
P
2
P
2
Pl
4
P
2
P
2
P
A B C
l
l
P
2
P
2
Questo significa che, fatta eccezione per travi di luce molto modesta, la sollecitazione che comanda
il dimensionamento di una trave inflessa è il momento flettente. Solo travi di luce modesta in cui il
momento flettente sia molto basso, possono raggiungere il collasso per taglio se vengono progettare
in base al solo momento flettente.
Vediamo adesso a quali tensioni dà origine il momento flettente.
Pl
2
P
2
P
2
1

1 SFORZI NORMALI IN UNA TRAVE INFLESSA
Una trave è un elemento strutturale soggetto prevalentemente a flessione e taglio.
Il momento flettente dà origine a sforzi normali σ proporzionali al momento agente M e distribuiti
linearmente lungo la sezione con valore massimo nelle fibre più distanti dall’asse neutro:
Lo sforzo ad una generica distanza y dall’asse neutro è fornito dalla formula di Navier:
σ =
M
I
y
Tale relazione mostra che gli sforzi normali dovuti al momento in una trave sono fortemente
influenzati dall’altezza h della trave: raddoppiando l’altezza gli sforzi diventano 4 volte più piccoli.
Invece se si raddoppia la larghezza b si ottiene solo un dimezzamento degli sforzi massimi.
Nel caso di una sezione rettangolare di base b e altezza h risulta:
1
I = bh
12
Quindi:
σ
max
3
M
= 3
bh
h M
= 2
2 bh
12 6
La grandezza
I bh
W = =
y 6
max
2
h
y max =
2
è il modulo di resistenza della sezione.
1.1 Esempio 1
Si determini il valore massimo dello sforzo in una trave a mensola di luce L=3m soggetta ad un
carico concentrato P=2.5kN, applicato all’estremo. Se la tensione massima che il materiale può
sopportare è fd=10N/mm 2 , la trave è in condizioni di sicurezza? Cosa accadrebbe agli sforzi se la
larghezza della sezione venisse raddoppiata e l’altezza mantenuta costante? E se l’altezza fosse
raddoppiata e la larghezza mantenuta costante?
Le dimensioni della sezione trasversale siano:
b=10cm, h=20cm,
Il massimo momento flettente si ha nella sezione di vincolo e vale:
M = PL = 2500N
⋅ 3m
= 7500Nm
max
In tale sezione il massimo sforzo vale:
2

σ
max
3
M max 6 ⋅ 7500Nm
⋅10
= =
2
1 2
bh
100mm
⋅ 200 mm
6
2
=
11.
25N
/ mm
La trave non è in condizioni di sicurezza perché risulta σmax>fd.
Se la larghezza della sezione fosse raddoppiata si avrebbe:
f b
M
=
bh
6
6 ⋅ 7500Nm
⋅10
200 ⋅ 200
3
max = 2
2 = 5.
625 N /
mm
2
La tensione diventerebbe la metà di quella iniziale e la trave sarebbe in condizioni di sicurezza.
Se l’altezza della trave fosse raddoppiata si avrebbe:
f b
M
=
bh
6
6 ⋅ 7500 ⋅10
100 ⋅ 400
3
max = 2
2 = 1.
4N
/
mm
2
Quindi la tensione diventerebbe circa 8 volte più bassa di quella iniziale. Quindi raddoppiare
l’altezza è molto più efficace rispetto a raddoppiare la larghezza anche se entrambe le scelte portano
alla stessa variazione di area della sezione trasversale (che raddoppia in entrambi i casi) e quindi
all’utilizzo della stessa quantità di materiale.
1.2 Esempio 2
Una trave appoggiata di luce 7.5m è soggetta ad un carico uniformemente distribuito q=9kN/m. Si
considerino tre tipi di sezione trasversale di uguale area (760mm 2 ) ma forma differente: rettangolare
(20mm x 38mm), circolare (r=15.55mm), triangolare(30.4mm x 50mm). Per quale delle tre sezioni
sono minimi gli sforzi dovuti alla flessione?
Il momento massimo è:
2
2
qL 9 ⋅ 7.
5
M max = = = 63.
28 kNm
8 8
I momenti di inerzia baricentrici per le tre sezioni sono:
rettangolare:
circolare:
triangolare:
3
3
bh 20 ⋅ 38
I = = = 91453mm
12 12
4
4
r 3.
14 ⋅15.
55
I = =
= 45897 mm
4 4
π
3
3
bh 30.
4 ⋅50
I = = = 105555 mm
36 36
Gli sforzi massimi quindi sono:
4
4
4
2
3

Rettangolare:
Circolare:
Triangolare:
f
f
f
f
b sup
b sup
b sup
b inf
=
=
=
=
f
f
b inf
b inf
M
I
M
I
E
E
M
=
I
c
c
=
sup
inf
M
I
E
E
63.
28 ⋅10
c =
91453
63.
28 ⋅10
c =
45897
63.
28 ⋅10
=
105555
63.
28 ⋅10
=
105555
6
6
6
6
38
= 13147 N / mm
2
15.
55
= 21439 N / mm
2
⋅ 50 = 19983 N / mm
3
1
⋅50
= 9991 N / mm
3
Quindi la sezione più efficiente è quella rettangolare (a parità di materiale fornisce gli sforzi
massimi più bassi). La sezione circolare ha momento di inerzia più basso perché ha più materiale
vicino all’asse neutro. La sezione triangolare ha momento di inerzia più altro delle altre due però il
valore di c è più elevato.
2
2
2
2
4

2 DIMENSIONAMENTO DELLA TRAVE
Scelto il materiale con cui realizzare la trave, se ne determina la tensione ammissibile per la
sollecitazione di flessione. Le dimensioni della sezione sono determinate facendo in modo che il
massimo sforzo flessionali nella trave sia inferiore a quello ammissibile:
σ max
quindi:
M
= ymax
≤
I
I
W = ≥
y
max
M
f d
f d
W prende il nome di modulo di resistenza a flessione.
Il progetto consiste nel trovare una sezione che abbia W uguale o maggiore di quello strettamente
necessario pari a M/fd.
Tuttavia ai fini del dimensionamento delle travi inflesse spesso sono più vincolanti le esigenze di
limitazione della deformabilità rispetto a quelle di resistenza.
2.1 Esempio 3
Una trave appoggiata agli estremi di legno (fd=11N/mm 2 ) con l=3m è soggetta ad una forza
concentrata in mezzeria pari a P=8000N. Progettare l’altezza della trave nelle ipotesi che la sezione
abbia larghezza b=50mm e b=100mm?
PL 8000 ⋅3
M max = = = 6000
4 4
W
nec
=
M
f
d
Nm
3
6000 ⋅10
Nmm
=
= 545454mm
2
11 N / mm
Il modulo di resistenza di una sezione rettangolare è:
bh
W =
6
2
Quindi l’altezza necessaria della trave si trova imponendo che sia:
W
h
h
nec
nec
nec
bh
=
6
2
nec
= 545454 mm
3
3
6Wnec
6 ⋅ 545454mm
= =
= 256mm
se la base è di 50mm
b 50mm
3
6Wnec
6 ⋅545454mm
= =
= 180mm
se la base è di 100mm
b 100mm
3
5

Le aree corrispondenti nei due casi sono: 50mm x 260mm=130cm 2;
100mm x 180mm=180cm 2
Quindi si ottiene una sezione più efficiente scegliendo una base minore e un’altezza maggiore.
Questa conclusione però non tiene conto del fenomeno dello “svergolamento”.
Inoltre non sono state condotte verifiche di deformabilità.
3 LIMITI DI DEFORMABILITÀ
Oltre a resistere ai carichi applicati le travi devono essere in grado di sopportare i carichi applicati
deformandosi limitatamente. I limiti sia per gli spostamenti totali (δmax) sia per quelli dovuti ai soli
sovraccarichi, sono definiti dalle norme e quelli fissati dalle norme europee sono riportati nella
tabella in figura:
dove:
δ max = spostamento totale;
δ 1 = spostamento dovuto ai soli carichi permanenti;
δ 2 = spostamento dovuto ai soli sovraccarichi;
δ 0 = spostamento dovuto alla (eventuale) contromonta;
3.1 Esempio 5
Dimensionare la trave in figura utilizzando un materiale con fd=355N/mm 2 .
6

Si assumano i seguenti valori:
carichi permanenti: g=15kN/m;
carichi variabili: q=10kN/m
l=8m.
Dimensionamento della sezione per flessione
1 . 4 g
l
1
.
5 q
Il momento massimo positivo si ha in mezzeria ed è pari a:
2
2
l
64m
M max =
288
8
8
( 1.
4g
+ 1.
5q)
= 36kN
/ m ⋅ = kNm
Progettiamo la sezione per flessione in funzione del massimo momento:
W
min
M
=
f
max
d
6
288 ⋅10
Nmm
=
= 811267mm
2
355N
/ mm
3
≅ 811cm
Scelgo un profilo IPE400 (W=1160cm 3 , I=23130cm 4 , p=0.663N/mm).
Verifiche di deformabilità
I limiti di spostamento sono:
1 1
ulim, tot = l = 8000mm
= 32mm
250 250
1 1
ulim, q = l = 8000mm
= 22.
8mm
350 350
La massima freccia della trave è:
u
tot
u q
=
=
5
384
5
384
( g + g
4
ql
=
EI
p
EI
5
384
+ q)
l
4
=
5
384
4 4
25.
663N
/ mm ⋅8000
⋅ mm
2
4
210000N
/ mm ⋅ 23130 ⋅10
mm
4
10N
/ mm ⋅8000
⋅ mm
2
210000N
/ mm ⋅ 23130 ⋅10
Quindi le verifiche di deformabilità sono soddisfatte.
3.2 Esempio 6
4
4
mm
4
3
4
= 10.
98mm
= 27.
4mm
Dimensionare la trave in figura utilizzando un materiale con fd=355N/mm 2 .
7

Si assumano i seguenti valori:
carichi permanenti: g=15kN/m;
carichi variabili: q=10kN/m
l=8m.
ls=2m
l s
l
1 . 4 g
1 . 5 q
Si tratta della stessa trave dell’esempio precedente nella quale però sono stati collocati due sbalzi
agli estremi. Lo schema statico della trave è equivalente al seguente nel quale non sono state
riportate le azioni verticali trasmesse dallo sbalzo perché non hanno influenza sulle sollecitazioni
nella trave.
1
( 1 . 4 g + 1 . 5 q ) l
2
Dimensionamento della sezione per flessione
2
s
Il momento massimo negativo si ha agli appoggi ed è pari a:
2
2
−
ls
4m
M =
72
max
2
2
( 1.
4g
+ 1.
5q)
= 36kN
/ m ⋅ = kNm
1 . 4 g
1
2
( 1 . 4 4g
g +
1 . 5 5q
q ) l s
2
1 . 5 q
Il momento massimo positivo si ha ancora in mezzeria ma è inferiore a prima ed è pari a:
2
2
+
l
ls
M =
216
max
8
2
( 1.
4g
+ 1.
5q)
− ( 1.
4g
+ 1.
5q)
= 288kNm
− 72kNm
= kNm
Progettiamo la sezione per flessione in funzione del massimo momento:
W
min
M
=
f
max
d
6
216 ⋅10
Nmm
=
= 608450mm
2
355N
/ mm
3
l
≅ 609cm
Scelgo un profilo IPE330 (W=713cm 3 , I=11770cm 4 , p=0.491N/mm).
Verifiche di deformabilità
I limiti di spostamento sono gli stessi di prima:
3
l
s
8

1 1
ulim, tot = l = 8000mm
= 32mm
250 250
1 1
ulim, q = l = 8000mm
= 22.
8mm
350 350
Il massimo abbassamento in mezzeria si può calcolare applicando il principio di sovrapposizione
degli effetti:
M
M
B
Tenendo conto che nel caso considerato:
M =
p
risulta:
f M
Quindi:
u
tot
u q
2
ls
2
l s =
2 2
pl l
= ⋅ =
32 8EI
l
4
1
256
pl
EI
4
=
p
l
=
+
f
f
p
M
2
p ⎛ l ⎞ pl
M = ⎜ ⎟ =
2 ⎝ 4 ⎠ 32
0.
0039
pl
EI
4
5 ( g + g p + q)
l
=
384 EI
4
( g + g p + q)
l
− 0.
0039
EI
4
( g + g p + q)
l
= 0.
0092
EI
4 4
25.
491N
/ mm ⋅8000
⋅ mm
0.
0092
2
4 4
210000N
/ mm ⋅11770
⋅10
mm
= 38.
86mm
=
5
384
4
ql
−
EI
0.
0039
4
ql
=
EI
0.
0092
4
2
C
M
4
10N
/ mm ⋅8000
⋅ mm
2
210000N
/ mm ⋅11770
⋅10
4
4
M
f p
mm
5pl 384EI
4
5pl =
384EI
4
=
f M
4
2
Ml
=
8 EI
=
= 15.
24mm
Quindi la verifica di deformabilità rispetto ai carici accidentali è soddisfatta mentre quella rispetto
ai carichi totali no.
9

Per ridurre la freccia dovuta ai carichi totali ad un valore ammissibile bisogna scegliere un profilo
che abbia momento di inerzia almeno pari a:
I
min
4
4 4
( g + g p + q)
l ( 15 + 0.
491 + 10)
N / mm ⋅8000
mm
= 0. 0092
= 0.
0092
= 14294cm
2
Eu
210000N
/ mm ⋅ 32mm
lim, tot
Si sceglie un IPE360 (W=904cm 3 , I=16270cm 4 , p=0.571N/mm) tutte le verifiche risultano
soddisfatte.
Quindi aggiungendo agli estremi della trave due sbalzi di luce pari ad ¼ della luce della trave si può
ridurre l’altezza della trave stessa da 400mm a 360mm.
4
10

4 INSTABILITÀ PER SVERGOLAMENTO
Consideriamo la trave in figura
La regione superiore della trave è in compressione.
Una trave non rigida lateralmente puòo instabilizzarsi,
inflettendosi lateralmente, a causa delle forze di
compressione presenti.
L’applicazione di un carico può causare lo sbandamento laterale (svergolamento) che avviene se si
instabilizza la parte compressa della sezione trasversale. Tale sbandamento avviene se la trave non è
sufficientemente rigida in direzione trasversale e può essere prevenuto utilizzando controventi
trasversali oppure rendendo più rigida la trave in direzione trasversale.
Nel caso in cui la trave sostenga un impalcato o un sistema di travi secondarie il controventamento
orizzontale viene fornito automaticamente da questi elementi. In caso contrario è necessario
irrigidire la trave in direzione trasversale incrementando le dimensioni della parte compressa della
trave.
4.1 Esempio 4
Una trave a sbalzo di 3m di lunghezza sostiene un carico concentrato di 4.5kN al suo estremo
libero. Si determinino le dimensioni richieste per la sezione trasversale rettangolare assumendo la
tensione ammissibile pari a famm=8.2MPa.
Il momento massimo è:
M = PL = 4.
5 ⋅ 3=
13.
5kNm
max
Il valore minimo del modulo di resistenza è:
W
nec
W nec
=
M
f
bh
=
6
max
amm
2
6
13.
5⋅10
Nmm
3
=
= 1646341mm
= 1646 cm
2
8.
2 N / mm
= 1646 cm
3
Quindi sono adeguate le sezioni rettangolari per le quali:
2
bh ≥
9876 cm
3
Le sezioni seguenti sarebbero tutte adeguate in termini di resistenza ma non sono tutte accettabili in
assenza di controventamento.
Quindi con le ultime due sezioni se da una parte si incrementa l’efficienza perché si riduce l’area
della sezione ( e quindi la quantità di materiale), dall’altra, la necessità del controventamento, rende
3
11

le soluzioni meno efficienti perché richiede l’utilizzo di ulteriore materiale.
Nel caso in cui il controventamento sia già offerto dal solaio o da travi secondarie conviene senza
dubbio utilizzare travi alte e strette. Negli edifici residenziali vengono di solito utilizzate travi con
rapporto h/b compreso tra 5 e 7.
b [cm] h [cm] Area [cm 2 ] h/b Controventamento
laterale
50 14.5 725 0.3 Non necessario
25 20 500 0.8 Non necessario
12.5 28.5 356.25 2.3 Non necessario
9 33.5 301.5 3.7 Necessario
5 45 225 9.0 Necessario
12

5 SFORZI TANGENZIALI IN UNA TRAVE INFLESSA
Il taglio T agente sulla sezione trasversale di una trave dà origine a sforzi tangenziali che possono
essere calcolati mediante la formula di Jourawski
*
S
τ h = T
Ib
dove:
S*=momento statico della porzione di sezione delimitata dal contorno e dalla fibra in
corrispondenza della quale si calcola la tensione;
I = momento di inerzia di tutta la sezione rispetto all’asse neutro;
b= larghezza della corda in corrispondenza della quale si calcola la tensione;
La variazione della tensione τ lungo la sezione trasversale dipende quindi dal rapporto S*/b
Per una sezione di larghezza b costante lo sforzo tangenziale massimo si verifica dove è massimo il
momento statico S*.
Questo avviene in corrispondenza dell’asse baricentrico che, se la sezione è soggetta a solo
momento flettente (in assenza di azione assiale), coincide con l’asse neutro.
Per una sezione rettangolare di dimensioni b x h si ha:
τ h
*
S
= T
Ib
Per y=0
=
2
T ⎛ h ⎞⎡
1 ⎛ h ⎞⎤
T ⎛ h 2 ⎞
b⎜
− y ⎟⎢
y + ⎜ − y ⎟⎥
= ⎜ − y ⎟
Ib ⎝ 2 ⎠⎣
2 ⎝ 2 ⎠⎦
I ⎝ 4 ⎠
T
h
I
= τ
Per y=±h/2 τ = 0
h
2
h
4
E tra questi limiti varia parabolicamente.
Ricordando che
I =
3
bh
12
V
τ h,
max = 3
bh
12
2
h 3 V 3
= = τ m
4 2 bh 2
= 1.
5τ
Ossia il massimo sforzo di taglio è 1.5volte lo sforzo di taglio medio.
m
13

5.1 Esempio 7 (vd Shodek)
Per la sezione in figura determinare la tensione tangenziale all’interfaccia tra la flangia superiore e
l’anima assumendo T=9kN.
1) Nel caso fosse utilizzata colla per assemblare gli elementi tra loro, quale sarebbe lo sforzo nella
colla?
2) Se venissero utilizzati dei chiodi disposti con un passo di 5cm, quale sarebbe lo sforzo in ciascun
chiodo?
3) Quale sarebbe il massimo sforzo tangenziale presente nella sezione trasversale?
1) Per valutare il valore dello sforzo in corrispondenza dell’interfaccia tra i due rettangoli
utilizziamo la formula trovata:
τ =
*
S
T
Ib
Dove S * è il momento statico dell’ala rispetto all’asse neutro (baricentrico) della sezione.
La posizione del baricentro si determina dividendo la sezione in due rettangoli:
y G
5⋅
30 ⋅15
+ 25 ⋅5
⋅ 32.
5
=
= 22.
95cm
= 229.
5mm
5⋅
30 + 25⋅
5
3
( 120.
5 − 25)
mm 1193750
*
S = mm ⋅ 50mm
⋅
=
250 mm
Il momento di inerzia della sezione rispetto all’asse neutro è:
3
3
5 ⋅30
2 25 ⋅5
2
I = + 5 ⋅30
⋅ ( 15 − 22.
95)
+ + 25 ⋅ 5 ⋅ ( 32.
5 − 22.
95)
12
12
=
4
11250 + 9480.
375 + 260.
41+
11400.
3125 = 32391cm
4
= 32391⋅10
mm
quindi:
4
14

τ
int erf
*
S
= T =
Ib
1193750mm
32391⋅
10 mm ⋅ 50mm
3
3
9 ⋅10
N ⋅
4 4
2
= 0.
66N
/ mm
Quindi la colla deve essere in grado di sostenere questo sforzo.
2) Se gli elementi fossero assemblati tramite chiodatura, ciascun chiodo dovrebbe essere in grado di
assorbire la forza risultante dagli sforzi di taglio su una superficie pari a quella di influenza del
chiodo. L’area di influenza di ciascun chiodo, essendo I chiodi posti ad interasse di 5cm è:
A ch
= 50mm ⋅5cm
= 2500mm
2
2
2
La forza risultante è: = A τ = 2500mm
⋅ 0.
66N
/ mm = 1650N
Fch ch int er
Quindi ciascun chiodo dovrebbe essere in grado di sopportare tale forza.
3) Il massimo sforzo di taglio agente sulla sezione trasversale si ha in corrispondenza della fibra
baricentrica. Il momento statico in corrispondenza di tale fibra vale:
S
*
= 250 ⋅50
⋅
= 1318006mm
( ) ( )
( 120.
5 − 50)
120.
5 − 25 + 50 ⋅ 120.
5 − 50
3
2
= 1193750 mm
3
+ 124256.
25mm
Questo momento statico avremmo potuto calcolarlo più facilmente con riferimento all’area inferiore
rispetto all’asse neutro:
229.
5
50 1316756.
25mm
2
*
S = ⋅ 229.
5 ⋅ =
3
I due valori vengono leggermente diversi a causa dell’approssimazione della posizione del
baricentro (a rigore 229.54545mm).
Il valore della tensione in corrispondenza della fibra baricentrica è quindi:
τ
bar
*
S
= V =
Ib
1318006mm
32391⋅10
mm ⋅ 50mm
3
3
9 ⋅10
N ⋅
4 4
2
= 0.
73N
/ mm
6 SFORZI PRINCIPALI
Gli sforzi flessionali e di taglio si combinano tra loro e producono degli sforzi risultanti di trazione
o di compressione chiamati sforzi principali che agiscono in direzioni diverse da quelle in cui
agiscono individualmente gli sforzi flessionali e di taglio.
Consideriamo per esempio una trave a sbalzo soggetta ad un carico concentrato all’estremo libero.
Sulle varie fibre della trave si hanno situazioni diverse:
• sulla fibra superiore vi sono solo sforzi di trazione;
• sulla fibra inferiore vi sono solo sforzi di compressione;
• sulla fibra baricentrica vi sono solo sforzi di taglio;
• sulle fibre intermedie vi sono entrambi gli sforzi.
3
=
15

A
B
C
B
A
A
B
C
B
A
Sforzi principali di trazione
Sforzi principali compressione
f v
f v
f t
f t
(a) Agli estremi liberi (superiore ed inferiore)
della trave, possono essere presenti solo
sforzi flessionali. Gli sforzi principali di
compressione e di trazione, quindi,
agiscono orizzontalmente e verticalmente
in questi punti.
(b) Nei punti intermedi della trave sono presenti
sia sforzi flessionali che di taglio.
La direzione degli sforzi principali dipende
dalla grandezza relativa di tali sforzi.
(c)
In corrispondenza dell'asse neutro della
trave, sono presenti solo sforzi di taglio.
Questi determinano le direzioni degli sforzi
principali, che formano quindi un angolo
di 45 gradi con l'orizzontale.
In ogni punto si può determinare la direzione degli sforzi principali di trazione e di compressione.
Indicando in ogni punto della trave la direzione di tali sforzi si ottengono delle curve che
rappresentano la traiettoria degli sforzi.
In figura sono riportate le traiettorie degli sforzi principali in una trave appoggiata:
Direzione degli sforzi principali
di compressione
Direzione degli sforzi principali
di trazione
Comportamento ad arco
Comportamento a fune
Gli sforzi principali possono avere valore diverso da un punto all’altro della trave ossia le curve in
figura collegano punti nei quali la tensione principale ha lo stesso segno (trazione o compressione)
ma può avere valore diverso da un punto all’altro.
16

Nelle verifiche di resistenza bisognerebbe considerare la situazione più sfavorevole dovuta a tutte le
tensioni presenti (normali e tangenziali) quindi dovremmo sapere dove e come calcolare il valore
massimo degli sforzi principali.
Più semplicemente le norme impongono di verificare la resistenza a taglio e flessione in un punto
della sezione in cui agiscano σ e τ, mediante la relazione:
σ
id
=
2 2
σ + 3τ ≤
6.1 Esempio 8
f
d
Consideriamo la trave vista nell’esempio 6 e verifichiamola considerando la presenza del taglio.
g=15kN/m; q=10kN/m l=8m. ls=2m
l s
l
1 . 4 g
1 . 5 q
profilo IPE 360 (W=904cm 3 , I=16270cm 4 , p=0.571N/mm)
Il taglio massimo si ha in corrispondenza degli appoggi:
( 1.
5g
+ 1.
5g
+ 1.
4q)
=
p
2
l
+ ( 1.
5g
+ 1.
5g
p + 1.
4q)
l =
37.
3565kN
/ m ⋅8m
+ 37.
3565kN
/ m ⋅ 2m
≅ 225kN
2
T s
In questa sezione oltre al taglio c’è anche un momento pari a 74.713kN kNm.
Nella sezione trasversale le fibre più sollecitate sono 3:
1) quella in cui è massima la tensione normale (fibre estreme della sezione:
M
W
74.
713⋅10
kNm
904 ⋅10
mm
6
σ max = =
3 3
2
≅ 83 N / mm τ = 0
La formula di Von Mises fornisce:
σ =
σ
2
id d
σ ≤ f
(verificata)
2) quella in cui è massima la tensione tangenziale (fibra baricentrica).
Il momento statico della porzione di sezione al di sopra della fibra baricentrica è pari a:
( 180 − 6.
35)
2 ( 180 −12.
7)
3
*
S = ⋅12.
7 ⋅
+ 8 ⋅
=
170 466203mm
2
La tensione tangenziale vale:
l
s
17

τ
max
TS
=
Ib
*
3
225 ⋅10
N ⋅ 466203mm
=
4 4
16270 ⋅10
mm ⋅8mm
La formula di Von Mises fornisce:
σ =
id
2
3τ
3
2
= 80.
6N
/ mm
f d 355
2
τ ≤ = = 204 N / mm
(verificata)
3
3
3) quella di attacco ala-anima in cui vi sono entrambe le tensioni con valore prossimo al
massimo.
La tensione normale si può determinare sfruttando la linearità del diagramma:
σ : σ max = −
( 180 12.
7)
: 180
σ =
83⋅
167.
3
=
180
77.
14
N / mm
La tensione tangenziale si calcola con la formula di Jourawski tenendo conto che il
momento statico dell’ala rispetto all’asse neutro vale:
3
( 180 − 6.
35)
374910
*
S = ⋅12.
7 ⋅
=
τ
max
170 mm
TS
=
Ib
*
3
255 ⋅10
N ⋅ 374910mm
=
4 4
16270 ⋅10
mm ⋅8mm
3
=
73.
44
N / mm
Si effettua la verifica utilizzando la relazione di Von Mises:
2 2
2
2
2
σ id = σ + 3τ = 77.
14 + 3⋅
73.
44 = 148N
/ mm (verificata)
Se non si vogliono calcolare i valori precisi si può fare direttamente la verifica considerando
i valori massimi:
σ
id
=
2
2
2
83 + 3⋅
80.
6 = 162 / mm
Se è verificata questa, sicuramente lo sono tutte le altre; se invece questa non è verificata
conviene tornare indietro e calcolare i valori precisi.
BIBLIOGRAFIA
Bernuzzi C. “Proporzionamento di strutture in acciaio”. Capitolo 4
Daniel L. Schodek. “Strutture”. Capitolo 6
2
2
18