Identificazione dei Modelli e Analisi dei Dati 27/3/1998

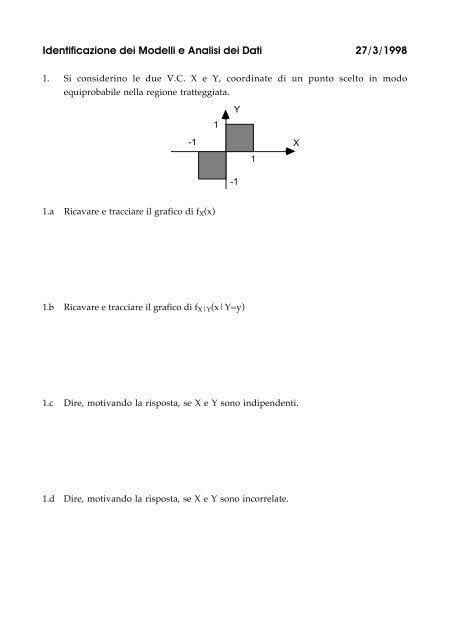
Identificazione dei Modelli e Analisi dei Dati 27/3/19981. Si considerino le due V.C. X e Y, coordinate di un punto scelto in modoequiprobabile nella regione tratteggiata.1Y-11X-11.a Ricavare e tracciare il grafico di f X (x)1.b Ricavare e tracciare il grafico di f X|Y (x|Y=y)1.c Dire, motivando la risposta, se X e Y sono indipendenti.1.d Dire, motivando la risposta, se X e Y sono incorrelate.

2. Si supponga che l'arrivo dei clienti allo sportello di una banca sia modellizzabiletramite degli eventi di Poisson con frequenza media λ = 1 cliente/minuto. Dueimpiegati (di seguito indicati con A e B) fanno la seguente scommessa: se ilprossimo cliente arriva dopo più di 1 minuto, A paga s dollari a B. Viceversa, se ilprossimo cliente arriva dopo T minuti, con T ≤ 1, B paga T dollari ad A (nota: T èun numero reale). Si indichi con V la V.C. vincita di A (che può assumere valorinegativi). Per comodità, si definiscano anche i due eventi A e B:A: l'impiegato A vince la scommessa (T ≤ 1 ⇒ V = T dollari)B: l'impiegato B vince la scommessa (T > 1 ⇒ V = -s).2.a Calcolare P(A) e P(B).2.b Calcolare e tracciare il grafico di f V|B (v|B) (la ddp della vincita V sotto l'ipotesiche T > 1).2.c Calcolare e tracciare il grafico di f V|A (v|A) (la ddp della vincita V sotto l'ipotesiche T ≤ 1). (Attenzione: se si verifica A, risulta 0 ≤ V ≤ 1)

2.d Calcolare e tracciare il grafico di f V (v).3. Si considerino due V.C congiunte X e Y con E[X] = E[Y] = 0, Var[X] = Var[Y] = 1,Cov[X,Y] = 0.5. Dato un numero reale, si definisca Z = X+aY. Determinare a inmodo tale che Cov[X,Z] = 0.

4. Dire se le seguenti affermazioni sono vere o false:(Punteggio: risposta esatta = 1, errore = -1, non risponde = 0)• Dati due eventi A,B tra di loro indipendenti, risulta sempreP(A+B) = P(A)+P(B).V❑F❑• Dati due eventi A,B con P(B) ≠ 0, risulta sempre P(A) = P(A|B)P(B).❑❑• La probabilità di avere almeno un successo su n prove di Bernoulli èpari a 1-(1-p) n .• Siano X,Y due V.C. indipendenti. Allora,Var[X+Y-E[X]-E[Y]] = σ X 2 +σ Y 2 .• Date due V.C. congiunte X,Y risulta Var[X+Y] = Var[X]+Var[Y] se esolo se X e Y sono incorrelate.• Data una V.C. X ed un numero reale a>0, si definisca Y = X/a. Allora,f Y (y) = f X (y/a)/a.• Date due V.C. congiunte X,Y, si supponga che la densitàcondizionata f Y|X (y|X=x) sia ben definita. Alloraf X (x) = ∫f Y|X (y|X=x)f Y (y)dy-∞+∞• Date due V.C. X, Y tra di loro indipendenti, si consideri una genericafunzione di V.C. Z = g(X,Y). Allora, E[Z]=g(E[X],E[Y]).• Siano X k , k = 1,…,N, delle V.C. i.i.d. con E[X k ] = m < +∞; allora, laloro media campionaria, per N → ∞, converge in probabilità ad m.❑❑❑❑❑❑❑❑❑❑❑❑❑❑• Siano X e Y due V.C. congiunte tra di loro incorrelate. Allora,f XY (x,y) = f X (x)f Y (y).❑❑

Identificazione dei Modelli e Analisi dei Dati 30/6/19981. Dire se le seguenti affermazioni sono vere o false:(Punteggio: risposta esatta = 1, errore = -1, non risponde = 0)• Dato un P.C. stazionario x(·), risulta sempre γ xx (2k) ≥ 0, k = 0,1,…,.• Sia (G(z),σ 2 ) un fattore spettrale non canonico di un P.C. stazionario.Allora, la varianza dell'errore di predizione ad un passo è sempremaggiore di σ 2 .• Se il fattore spettrale canonico Ĝ(z) di un P.C. gaussiano a spettrorazionale non ha zeri con modulo unitario, il predittore ottimo a kpassi è stabile.• Un segnale persistentemente eccitante di ordine m lo è anche diordine m-1.• Sia y(t) = Zsin(t), dove Z ~ G(0,1). Allora y(·) è un P.C. stazionario.• Sia Y(z) = H(z)X(z) dove H(z) è stabile e x(·) è un P.C. stazionario(scalare). Se H(z)H(z -1 ) = Φ xx (z) -1 , allora y(·) è un rumore bianco.• Sia x(·) un P.C. stazionario con E[x(t)] = 0. Allora, per |τ| < N,N-|τ|γˆxx (τ) = 1 N ∑x(i)x(i+τ)i=1è uno stimatore polarizzato della γ xx (τ).• Sia y(t) = x(t)+w(t), dove w(·) è un rumore bianco e x(·) è un P.C.stazionario, indipendente da w(·), con fattore spettrale canonico Ĝ(z).Allora, i poli del fattore spettrale canonico di y(·) appartengonoall'insieme dei poli di Ĝ(z).• Per un AR(1), risulta ŷ(t+2|t) = 0.• Sia y(·) un P.C. stazionario ottenuto come l'uscita di un ARalimentato da un rumore bianco w(·) con E[w(t)] = m w ≠ 0. Allora,risulta sempre E[y(t)] ≥ m w .V❑❑❑❑❑❑❑❑❑❑F❑❑❑❑❑❑❑❑❑❑

2. Si scriva sopra il grafico degli spettri il numero del corrispondente fattorespettrale (in tutti e quattro i casi σ 2 = 1)1. G(z) = 1 + 0.5z -1 2. G(z) = 1 - 0.5z -13. G(z) = 1 + 0.9z -1 4. G(z) = 1 - 0.9z -14433spettro2spettro21100 2 4w00 2 4w2.52.522spettro1.51spettro1.510.50.500 2 4w00 2 4w

3. Scrivere sopra ciascuna realizzazione di P.C. stazionario il numero che identificail corrispondente grafico dell'autocovarianza12n.115n.21010gamma(t)86gamma(t)504-52-50 0 50tn.310.8-10-50 0 50tn.464gamma(t)0.60.4gamma(t)200.2-20-50 0 50t-4-50 0 50t10542y0y0-5-2-100 50 100t10-40 50 100t550y0y-5-5-100 50 100t-100 50 100t

4. Si consideri il seguente processo casualey(t) = 0.6y(t-1) + 2v(t) + v(t-1) ,v(·) ~ WGN(0,1)4.a Ricavare l'espressione nel dominio del tempo del predittore ottimo a due passi.4.b Calcolare la varianza dell'errore di predizione a due passi.

Identificazione dei Modelli e Analisi dei Dati 21/7/19981. Si considerino due V.C congiunte X,Y distribuite in modo uniforme nel triangoloin figuraY1X1.a Calcolare la funzione di distribuzione della V.C. Z = Y/X.1.b Calcolare la ddp di Z.12. Sia X una V.C. discreta. Dimostrare che Var[X] = 0 implica P(X=E[X])=1.3.a Si dia la definizione di segnale persistentemente eccitante (p.e.) di ordine n.3.b Dimostrare che un rumore bianco è p.e. di ogni ordine (con probabilità uno).4. Si consideri il seguente schema blocchi in cui G(z) = 1+0.5z -1 , H(z) = z -1 +0.1z -2WN(0,1)H(z)WN(0,1)G(z)++y4.a Supponendo che i due rumori bianchi siano indipendenti tra loro, calcolare lavarianza del P.C. stazionario y(·).4.b Ricavare lo spettro e la funzione di autocovarianza di y(·).

Identificazione dei Modelli e Analisi dei Dati 15/9/19981. Un automobilista viola quotidianamente un divieto di svolta al fine di accorciarel'itinerario di ritorno a casa dal lavoro. Infatti, ritiene che sia molto bassa laprobabilità p di essere multato da un vigile quando si commette tale infrazione.Si indichi con x k la probabilità di farla franca k giorni di seguito. Suppponendop = 0.001, calcolare per quali valori di k risulta x k = 0.5 e x k = 0.05.2. Si supponga di avere a disposizione su un computer un generatore di numericasuali che produce realizzazioni di una V.C. U uniforme in [0,1]. Dire,motivando la risposta, quali operazioni bisogna effettuare per ottenererealizzazioni di una V.C. esponenziale con parametro λ.3. Si esponga sinteticamente (max. 1 pagina) il metodo della stima dello spettro diun P.C. stazionario basato sul periodogramma.4. Si consideri il seguente schema blocchi in cui y(·) è un P.C. stazionario eG(z) = 1/(1+az -1 ) è la fdt di un AR(1).WN(0,1)WN(0, σ 2 )G(z)++ySapendo che Var[y(t)] = 11/3 e che Γ yy (0) = 5, determinare i valori di a e σ 2 .

Identificazione dei Modelli e Analisi dei Dati 29/9/19981. Si considerino due V.C congiunte X,Y distribuite in modo uniforme nella zonaindicata in grigio nella figura:Y1-1X11.a Calcolare la funzione di distribuzione della V.C. Z = X+Y.1.b Calcolare la ddp di Z.-12.a Dare la definizione di eventi di Poisson.2.b Dire come è distribuito il tempo di attesa tra un evento di Poisson e il successivo.(Non è richiesto di ricavare la distribuzione).2.b Relativamente agli eventi di Poisson, spiegare cosa si intende per proprietà di"non memoria"3. Spiegare concisamente (1 pagina al massimo) cosa si intende per metodi diidentificazione a minimizzazione dell'errore di predizione.4. Si consideri un P.C. stazionario y(·) che soddisfa l'equazioney(t) = 0.5y(t-1) + w(t-1) - 2w(t-2),w(·) ~ WN(0,1)4.a Ricavare il predittore ottimo ad un passo4.b Determinare la varianza dell'errore di predizione a due passi.

Identificazione dei Modelli e Analisi dei Dati 2/11/19981. Dato un numero reale α ed una V.C X, dimostrare cheE[(X-α) 2 ] = (E[X]-α) 2 +Var[X].2. Le località A e B siano collegate da due diversi percorsi come indicato in figura.CADB2.a Se si segue il percorso A-C-B, vi è una probabilità pari a 0.1 di trovare un ingorgostradale, nel qual caso si impiegano più di due ore per raggiungere B. Se non vi èingorgo i tempi di percorrenza dei tratti A-C e C-B sono V.C. indipendentientrambe distribuite uniformemente nell'intervallo 30'-60'. Calcolare laprobabilità di percorrere la strada A-C-B in meno di 90'.2.a Se si segue il percorso A-D-B, vi è una probabilità pari a 0.2 di trovare un ingorgostradale, nel qual caso si impiegano più di due ore per raggiungere B. Se non vi èingorgo i tempi di percorrenza dei tratti A-D e D-B sono V.C. indipendentidistribuite uniformemente in 30'-60' e 30'-40', rispettivamente. Calcolare laprobabilità di percorrere la strada A-D-B in meno di 90'.3.a Dare la definizione di segnale persistentemente eccitante di ordine n.3.b Fornire un esempio di segnale che è persistentemente eccitante di ordine 1 manon di ordine 2.4. Si considerino i processi casualix(t) = 0.7x(t-1) + w(t) ,y(t) = x(t) + v(t) ,w(·) ~ WN(0,1)v(·) ~ WN(0,1).con v(·) e w(·) indipendenti tra loro.4.a Calcolare γ yy (0) e γ yy (1).4.b Si definisca s(t) = ay(t-1). Trovare il valore di a che minimizza E[(y(t)-s(t)) 2 ].

Identificazione dei Modelli e Analisi dei Dati 8/2/19991. Si consideri una sequenza di V.C. X k indipendenti e identicamente distribuite.1.a Si enunci la Legge dei Grandi Numeri fornendo una condizione sufficienteaffinché essa valga.1.b Si enunci il Teorema Centrale del Limite fornendo una condizione sufficienteaffinché esso valga.2. Si considerino due V.C. X e Y tra di loro indipendenti distribuite in modouniforme tra -1 e +1. Determinare la d.d.p. della V.C. Z = X - Y3 Si consideri il problema della stima di un modello lineare nei parametri e sisupponga di doverne scegliere la complessità all'interno di classi di modelligerarchici (esempio: costante, retta, parabola, cubica, etc.). In altre parole, si trattadi decidere se i dati sono descritti "meglio" da una retta piuttosto che da unacostante o da una cubica, etc. Si discuta in non più di una pagina e mezza comepuò essere affrontato il problema.4 I pazienti affetti da diabete mellito insulino-dipendente misurano la loroglicemia tipicamente 3 volte al giorno. Indicando con y k la k-esima misura diglicemia e con v k il relativo errore di misura, l'andamento della serie delleglicemie può essere schematizzato come la somma di un trend lineare e di unacomponente ciclica (giornaliera):y k = θ 1 + θ 2 k + θ 3 sin(2πk/3) + θ 4 cos(2πk/3) + v kIpotizzando che gli errori di misura siano i.i.d. e gaussiani, si descriva, in non piùdi una pagina e mezza, una procedura per la stima dei parametri del modello edei loro intervalli di confidenza basata sul metodo della massimaverosimiglianza.5. Supponendo di avere a disposizione due serie temporali u k (ingressi) e y k (uscite),si descriva, in non più di una pagina, cosa è un modello ARX e come se nepossono stimare i parametri.6. Si consideri il seguente schema blocchi in cui G(z) = 1+0.5z -1 , H(z) = z -1 +0.6z -2WN(0,1)H(z)WN(0,1)G(z)++y6.a Supponendo che i due rumori bianchi siano indipendenti tra loro, calcolarespettro e autocovarianza del P.C. stazionario y(·).6.b Ricavare il predittore e due passi y(t+2|t) e la varianza del relativo errore dipredizione.

Identificazione dei Modelli e Analisi dei Dati 1/3/19991.a Dare la definizione di probabilità condizionata1.b Enunciare e dimostrare il teorema della probabilità totale.1.c Enunciare e dimosrare il teorema di Bayes.2. Siano X e Y due V.C. che rappresentano le coordinate di un punto scelto in modoequiprobabile nel quadrato disegnato in figura.1Y2.a Calcolare la ddp della V.C. V = max(X,Y).2.b Calcolare la ddp della V.C. W = min(X,Y).2.c Dire, motivando la risposta, se V e W sono indipendenti.13 Si consideri il problema della stima di un modello lineare nei parametri e sisupponga di doverne scegliere la complessità all'interno di classi di modelligerarchici (esempio: costante, retta, parabola, cubica, etc.). In altre parole, si trattadi decidere se i dati sono descritti "meglio" da una retta piuttosto che da unacostante o da una cubica, etc. Si discuta in non più di una pagina e mezza comepuò essere affrontato il problema.4. Si supponga di misurare la grandezza θ 1 mediante tre sensori. I primi dueforniscono delle misure non polarizzate affette da errori di misura v 1 , v 2 :XY 1 = θ 1 + v 1Y 2 = θ 1 + v 2v 1 ~ G(0,1)v 2 ~ G(0,1)Il terzo sensore invece è starato e fornisce una misura polarizzata, conpolarizzazione pari a θ 2 , ed è affetto da un errore di misura v 3 :Y 3 = θ 1 + θ 2 + v 3v 3 ~ G(0,4)Supponendo che gli errori di misura siano tutti indipendenti tra loro, ricavarel'espressione della stima ML di θ 1 e θ 2 in funzione di Y 1 , Y 2 , Y 3 (è sufficientericavare la formula risolutiva senza calcolare l'inversione di matrice).5. Descrivere il test di bianchezza dei "cambi di segno".6. Sia y(·) un P.C. stazionario tale cheE[y(t)] = 1 , γ yy (t) = 0.5τ0.75Trovare il fattore spettrale canonico ed il predittore a k passi.