Graphen-Algorithmen

Einführung
Matroid-Probleme in Graphen
Graphen-Algorithmen
Matroide und Greedy-Algorithmen
Dr. Tobias Baumann
14. Juni 2011
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Einführung
Heute geht es um die Frage, wo genau uns denn
Greedy-Algorithmen hilfreich sein können.
Greedy-Algorithmus
Gegeben ist eine Menge S, eine Mengenfamilie F ⊂ P(S) und eine
Bewertungsfunktion f : S → R. Gesucht ist eine Lösungsmenge
L ⊂ S mit L ∈ F , so dass ∑ s∈L f (s) = max H∈F f (h) gilt.
∑
h∈H
Der Greedy-Algorithmus wählt nun eine Startmenge L 0 und fügt zu
dieser Startmenge sukzessive ein Element s ∈ S mit maximalem
Wert unter allen zulässigen Elementen aus S, so dass die
resultierende Menge L i+1 ∈ F ist.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Greedy-Algorithmen
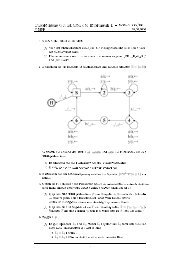
Wir betrachten noch einmal das MST-Problem:
Minimum / Maximum Spanning Tree
Gegeben ist ein zusammenhängender Graph G = (V , E, w) mit
Kantengewichten w : E → N. Gesucht ist ein Baum T , der alle
Knoten von G umfasst, und dessen Gewicht W = ∑ e∈T w(e)
minimal bzw. maximal über alle aufspannenden Bäume ist.
Wir können das Problem bereits in erwarteter linearer Zeit lösen,
aber das ist gerade gar nicht unser Ziel.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Algorithmus von Kruskal
1 T := ∅
2 While (T nicht zusammenhängend)
1 Wähle e ∈ E mit w(e) minimal, so dass in T ∪ {e} kein Kreis
entsteht.
2 Setze T := T ∪ {e}.
Der Algorithmus ist offensichtlich ein Greedy-Algorithmus.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Korrektheit
Wir wissen bereits aus DSEA, dass der Kruskal-Algorithmus
korrekt arbeitet. Das Schnittlemma bietet uns dort einen
schlüssigen Beweis.
Allerdings ist das Schnittlemma nur für aufspannende Bäume
geeignet. Greedy-Algorithmen funktionieren aber auch bei ganz
anderen Problemen!
Deshalb lernen wir heute einen allgemeinen Beweis für die
Korrektheit von Greedy-Algorithmen kennen.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Matroide
Definition
Sei S eine endliche Menge und F ⊂ P(S) eine Familie von
Untermengen von S. Das Paar M = (S, F ) heißt Matroid, falls
folgendes gilt:
∅ ∈ F
A ∈ F , B ⊆ A ⇒ B ∈ F
A, B ∈ F , |B| = |A| + 1 ⇒ ∃s ∈ B \ A : A ∪ {s} ∈ F
Eine maximale Menge in F heißt Basis des Matroids. Alle Basen
eines Matroids M enthalten dieselbe Anzahl Elemente r(M), der
Rang von M. Die Familie F wird auch als Familie der
unabhängigen Mengen bezeichnet. (Nicht zu verwechseln mit
unabhängigen Mengen in Graphen!) Sind nur die ersten beiden
Forderungen erfüllt, sprechen wir von Unabhängigkeitssystemen.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Was heißt das?
∅ ∈ F
A ∈ F , B ⊆ A ⇒ B ∈ F
A, B ∈ F , |B| = |A| + 1 ⇒ ∃s ∈ B \ A : A ∪ {s} ∈ F
Wir können jede Menge aus F durch Hinzunahme weiterer
Elemente zu einer Basis ergänzen.
Der Name Matroid erinnert an Matrizen:
Seien a 1 , ..., a n Vektoren aus einem m-dimensionalen Vektorraum.
Wir können die Vektoren als Spalten in einer m × n-Matrix sehen.
Nun ist S die Menge der Vektoren. Eine Teilmenge A ⊆ S ist
unabhängig, wenn die Vektoren in A linear unabhängig sind. Dann
ist die dritte Forderung gerade der Steinitzsche Austauschsatz der
Linearen Algebra. Der Rang ist dann die Dimension des
Unterraums, der von den Vektoren in S aufgespannt wird.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Grundlegende Eigenschaften
Alle Basen eines Matroids haben dieselbe Kardinalität.
⇐⇒
Sind X , Y ∈ F mit |X | > |Y |, so gibt es ein x ∈ X \ Y mit
Y ∪ {x} ∈ F .
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Was haben Graphen mit Matroiden zu tun?
Beim MST-Problem haben wir es mit einem Matroiden zu tun:
MST ↔ Matroid
Sei G = (V , E) ein Graph. Sei F ⊆ P(E) die Menge aller Wälder
in G. Dann ist M = (E, F ) ein Matroid.
Beweis
∅ ist ein Wald.
Ist A ein Wald, dann ist jede Teilmenge von A ein Wald.
Seien A, B zwei Wälder mit |A| + 1 = |B|. Weiter seien
A 1 , ..., A m die Komponenten von A mit den Knotenmengen
V 1 , ..., V m . Es gilt |A i | = |V i | − 1. Da nun |B| > |A| ist, muss
es eine Kante e ∈ B geben, die zwei verschiedene
Komponenten A s , A t miteinander verbindet. Somit ist A ∪ {e}
ein Wald.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Die Basis von M ist gerade die Menge der aufspannenden Wälder
von G, und der Rang von M ist |V | − t, wobei t die Anzahl der
Zusammenhangskomponenten von G ist.
Jetzt wissen wir, dass das MST-Problem auf Matroiden basiert.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Matroid und Greedy-Algorithmus
Satz
Der folgende Greedy-Algorithmus findet eine Basis minimalen
Gewichts in einem gewichteten Matroiden M = (S, F ) mit
Gewichtsfunktion w : S → R:
1 Setze A 0 := ∅.
2 Sei A i ⊆ S mit |A i | = i. Dann ist
X i = {x ∈ S \ A i : A i ∪ {x} ∈ F }. Ist X i = ∅, dann ist A i die
Basis und wir sind fertig.
Andernfalls wählen wir a i+1 ∈ X i mit minimalem Gewicht und
setzen A i+1 := A i ∪ {a i+1 }.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
MST
Matroide
Greedy-Algorithmus
Beweis
Sei A = {a 1 , ..., a r } das Ergebnis des Algorithmus. Aus den
Matroideigenschaften folgt, dass A eine Basis ist. Durch die
Konstruktion des Algorithmus ist w(a 1 ) ≤ w(a 2 )... ≤ w(a r ).
Sei nun B = {b 1 , ..., b r } eine Basis mit w(B) < w(A) und
w(b 1 ) ≤ ... ≤ w(b r ). Dann gibt es einen kleinsten Index i mit
w(b i ) < w(a i ). Es ist außerdem i ≥ 2. Wir betrachten die Mengen
A i−1 und B i = {b 1 , ..., b i }. Nach dem Austauschaxiom gibt es ein
b j ∈ B i \ A i−1 mit A i−1 ∪ {b j } ∈ F . Da aber
w(b j ) ≤ w(b i ) < w(a i ) ist, hätte der Greedy-Algorithmus im i-ten
Schritt b j statt a i gewählt. Widerspruch.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Matroide
Matching
Kürzeste Wege
Gibt es noch andere Graph-basierte Matroide?
Beispiel
Sei G = (V , E) ein Graph, I ⊆ V eine unabhängige Menge und
k : I → N 0 .
S = E
F = {X ⊆ S : d X (v) ≤ k(v)∀v ∈ I }.
Die Konstruktion M = (S, F ) ist ein Matroid.
Beweis
Forderungen 1 und 2 sind klar.
Seien X , Y ∈ F mit |X | > |Y |. Sei I ′ = {v ∈ I : d Y (v) = k(v)}.
Jetzt ist aber auch d X (v) ≤ k(v)∀v ∈ I ′ . Somit gibt es ein
e ∈ X \ Y mit e /∈ N(v) für v ∈ I ′ . Somit ist Y ∪ {e} ∈ F .
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Matroide
Matching
Kürzeste Wege
Beispiel
Sei G = (V , E) ein gerichteter Graph, T ⊆ V eine Knotenmenge
und k : T → N 0 .
S = E
F = {X ⊆ S : d − X
(v) ≤ k(v)∀v ∈ T }.
Die Konstruktion M = (S, F ) ist ein Matroid.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Matroide
Matching
Kürzeste Wege
Matchings in bipartiten Graphen
Definition
Sei G = (S ˙∪T , E ⊆ S × T ) ein bipartiter Graph. Wir suchen ein
Matching M ⊆ E, d.h. eine Kantenmenge, bei der die Kanten
paarweise nicht inzident sind.
Matchings können wir vergrößern, indem wir alternierende Pfade
suchen (s. eine der kommenden Vorlesungen).
Matroid?
Wir betrachten Knotenmengen X ⊆ S, die komplett gematcht
werden können. Eine solche Knotenmenge heißt Transversale.
Wir setzen M = (S, {X ⊆ S : X ist Transversale in G}). M ist ein
Matroid.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Matroide
Matching
Kürzeste Wege
Matching = Matroid
Beweis
Axiome 1 und 2 sind erfüllt.
Seien nun A und B Transversalen mit |B| = |A| + 1 und den
zugehörigen Matchings M A , M B . Das heißt, |M B | = |M A | + 1.
Daraus folgt nun, dass es einen alternierenden Weg gibt, der M A
vergrößert und in einem Knoten u ∈ B \ A beginnt.
Wir können also Matchingprobleme in bipartiten Graphen mit Hilfe
eines Greedy-Algorithmus lösen!
Wie man einen alternierenden Weg findet, sehen wir in einer der
folgenden Vorlesungen.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Kürzeste Wege in Graphen
Matroide
Matching
Kürzeste Wege
Definition
Sei G = (V , E, w) ein Graph mit nichtnegativen Kantengewichten
w : E → R + 0
und v, w ∈ V zwei Knoten. Gesucht ist der kürzeste
Weg von v nach w.
Wir können das Problem mit dem Dijkstra-Algorithmus lösen, der
in bester Greedy-Manier einen Kürzeste-Wege-Baum immer um die
kürzestmögliche Kante erweitert.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Matroide
Matching
Kürzeste Wege
Kürzeste Wege = Matroid?
Matroid?
Wir suchen also wieder einen aufspannenden Baum. Allerdings ist
das Unabhängigkeitssystem M = (S, F ) anders aufgebaut:
S ist wieder die Kantenmenge E.
A ∈ F , wenn A die Teilmenge eines Weges von v nach w ist.
Wir sehen also: die ersten beiden Forderungen eines Matroids sind
erfüllt. Allerdings kann man leicht Beispiele konstruieren, bei denen
die dritte Forderung nicht erfüllt wird.
Wir haben hier also keinen Matroid, sondern “nur” ein
Unabhängigkeitssystem.
Dr. Tobias Baumann
Matroide

Einführung
Matroid-Probleme in Graphen
Matroide
Matching
Kürzeste Wege
Kürzeste Wege = Matroid? II
Zweiter Versuch, diesmal mit Single Source Shortest Path:
S ist die Kantenmenge E.
A ∈ F , wenn A ein Baum ist, der v enthält.
Jetzt ist zwar die dritte Forderung erfüllt, aber die zweite nicht:
Wir können aus einem Baum A ∈ F Kanten so herausnehmen, dass
v isoliert wird.
Aber wir haben Glück: Ein solches Konstrukt wird auch Greedoid
genannt, das unter bestimmten Umständen ebenfalls einen
erfolgreichen Greedy-Algorithmus liefert.
Dr. Tobias Baumann
Matroide