5 cm 4 cm 3,5 cm 1,5 cm 37,1 ° 2,5 cm 1 cm 3,2 cm 2,5 cm

Prof. S. Krauter MODUL 2 – R. Geometrie SoSe 05. Blatt 2 – Lösungen
Aufgabe 1:
Bei der Zwei- und Dreitafelprojektion ist stets auf vorteilhafte Lage des Körpers zu
achten. In vielen Fällen bringt ein dritter Riss keine neuen Erkenntnisse.
Wichtig ist das Zusammenspiel der drei Risse: Zugeordnete Punkte befinden sich immer
auf entsprechenden Ordnerlinien.
Schrägbilder im Aufriss (Frontschau oder Kavalierprojektion):
• Man zeichnet die Front oder einen Mittenschnitt, der zur vertikalen Bildebene
parallel ist, in wahrer Größe.
• An diesen setzt man die senkrecht zur Bildebene nach vorn oder hinten
verlaufenden Kanten im gewählten Verzerrungswinkel und -verhältnis an.
Schrägbilder im Grundriss (Vogelschau oder Militärperspektive):
• Man zeichnet die Grund- bzw. Standfläche oder einen Mittenschnitt, der zur
horizontalen Bildebene parallel ist, in wahrer Größe.
• An diesen setzt man die senkrecht zur Bildebene nach oben oder unten
verlaufenden Kanten im gewählten Winkel zu einer Standlinie und im
gewählten Verkürzungsverhältnis an.
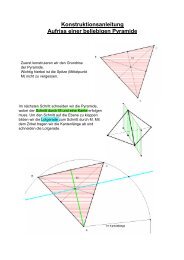
a) In der nachstehenen Zeichnung (Maßstab 1:200) wird die Giebelkante (=
Sparrenlänge) in wahrer Größe, also mit 5 m, abgebildet und ebenso die
Dachneigung von 37°.
2,5 cm
37,1 °
1,5 cm
3,5 cm
4 cm
5 cm
3,2 cm
1 cm
2,5 cm
Das Schrägbild in Vogelschau wird am einfachsten über dem Grundriss aufgebaut.
Das Schrägbild in Frontschau wird am einfachsten an den Aufriss angehängt.

) Siehe Aufgabe 2.
c) Siehe Aufgabe 4.
d) Siehe Zeichnung zu Teil a). Teil c) ist in der Farbe magenta hinzugefügt.
e) Haus gemäß Aufgabe a):
Das Haus ist eine Säule mit der Giebelfront als Grundfläche und der Hauslänge als
Säulenhöhe. Daher ist der Rauminhalt V = G * h = 68 m² * 10 m = 680 m³.
Die Dachfläche besteht aus zwei Rechtecken der Länge 10 m und der Breite 5 m
(Sparrenlänge), hat also den Flächeninhalt 100 m².
Alternative Überlegung: Die Dachfläche ist überall gleich zur Grundfläche geneigt
und zwar im Verhältnis 5 : 4 , wie man besonders gut am Seitenriss erkennt
(Sparrenlänge = 5 m gegenüber der halben Hausbreite mit 4 m). Daher misst die
Dachfläche das 5/4-fache der Grundfläche, also 5/4 * 80 m² = 100 m².
Haus gemäß Aufgabe d):
Hier ändert sich die Größe der Dachfläche nicht: Das Dach ist überall gleich
gegenüber der Grundfläche geneigt, also Dachfläche = 5/4 * 80 m² = 100 m².
Man kommt durch Zusammenstückeln der Einzelflächen (2 Trapeze und 2
gleichschenklige Dreiecke mit je 30 m² bzw. 20 m²) zum selben Ergebnis.
Das Volumen ist leicht zu bestimmen: Gegenüber dem Haus in a) fehlen zwei
Pyramiden mit der Giebelfläche als Grundfläche und der halben Hausbreite als
Höhe, also V’ = 2 * 1/3 * 12 * 4 m³ = 32 m³. Das Restvolumen beträgt also V =
648 m³.
Aufgabe 2:
Am besten wählt man eine Lage des Tetraeders, bei dem eine Grundkante in der
Grundrissebene senkrecht auf die Aufrissebene zuläuft. Dann erhält man im Aufriss die
Körperhöhe, die Seitenhöhe und die Seitenkante in wahrer Größe. Wir verzichten auf
die Wiedergabe des Dreitafelbildes und geben nur die Schrägbilder an.
Wir geben die Verhältnisse für ein reguläres Tetraeder mit Kantenlänge a allgemein an:
a
D
D
Seitenhöhe = h s = * 3 = 0,866… * a
4,9 cm
2
a
Körperhöhe = h k = * 6 = 0,816… * a
3
a
Seitenfläche = A s = * 3 = 0,433… * a²
4
Oberfläche = A = a² * 3 = 1,732… * a²
2
C
E
A
S
6 cm
4,9 cm
5,2 cm
B
A
E
C
S
5,2 cm
6 cm
B
a
Rauminhalt = V = * 2
12
3
= 0,11785… * a³
Aufgabe 3:
Das n-Ecks-Antiprisma hat als Grund- und Deckfläche je ein (i.A. regelmäßiges) n-Eck.
Die 2n Seitenflächen dagegen sind Dreiecke. Es besitzt 2n Ecken, 4n Kanten und 2n+2
Flächen.

a) Ein regelmäßiges Dreiecks-Antiprisma ist nichts anderes als ein regelmäßiges
Oktaeder. Dies kann aufgefasst werden als zwei mit den Grundflächen verklebte
regelmäßige quadratische Pyramiden.
b) Im nachfolgenden Dreitafelbild hat das Grunddreieck ABC den Mittelpunkt M und
das Deckdreieck DEF den Mittelpunkt N. Das Seitendreieck ABD ist im Grundriss
ausgeklappt (zum Grundriss parallel gedreht). Im Aufriss erscheint die Raute DQCP
(mit der Höhe P’Du’ der Seitendreiecke als wahrer Seitenlänge) in wahrer Größe.
Damit ist auch die Höhe des Antiprismas in wahrer Größe konstruiert.
F'''
D'''N'''Q'''
E'''
E''F''Q''
N''
D''
6,5 cm
6,9 cm
A'''
C'''M'''
B'''
C''
E'
M''
A''B''P''
B'
C'
Q'
8 cm
M'N'
P'
D'
Du'
Seitenlänge AB variabel
F'
A'
6,9 cm
a
c) Berechnungen: Die Seitenhöhe eines der Seitendreiecke beträgt h s = * 3 .
2
Die Körperhöhe des Antiprismas lässt sich berechnen aus dem Dreieck C’’M’’Q’’ zu
h
h k = s a
* 8 = * 6 = 0,8165… * a
3 3
d) Die Oberfläche besteht aus 8 kongruenten gleichseitigen Dreiecken der
2
a
Seitenlänge a, also A = 8 * * 3 = 0,433… * a².
4
Der Rauminhalt kann mit Hilfe der Auffassung von den zwei quadratischen
Pyramiden berechnet werden. Dazu muss jedoch die Höhe dieser Pyramiden, also
die Hälfte der Strecke EF berechnet werden:
EF ist die Diagonale im Quadrat AECF mit der Seitenlänge a, hat also die Länge
EF = a* 2 = 1,414 * a.
3
a
V = 2 * a² * 1/3 * a/2 * 2 = * 2 = 0,4714... * a³.
3

Aufgabe 4:
Regelmäßige Quadratische Pyramide mit Seitenkante = Grundkante = a:
Berechnungen:
a
Seitenhöhe h s = * 3 (Höhe im gleichseitigen Dreieck).
2
a a
Körperhöhe: Kathete im rw. Dreieck: h k ² = h s ² - ( )² = * 2 = 0,7171… * a
2 2
2
a
Oberfläche: A = a² + 4 * * 3 = a² * (1 + 3 ) = 2,732… * a².
4
a a
Volumen: V = 1/3 * a² * * 2 = * 2 = 0,2357… * a³.
2 6
3
7,08 cm
10 cm
10 cm
8,67 cm
Da die beiden Schrägbilder relativ einfach zu zeichnen sind, verzichten wir auf die
Wiedergabe. Wir empfehlen zur Übung die Darstellung der Pyramide in Frontschau,
wobei sie gegenüber der obigen Lage um 45° verdreht steht.