Teilgebiete der Abbildungsgeometrie - Mohr.lehrer.belwue.de

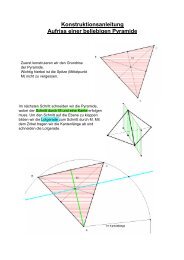
Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der GrundschuleTeilgebiete der AbbildungsgeometrieIn der Abbildungsgeometrie wird zur Klassifizierung von Eigenschaftendes Raumes (bzw. der Ebene) und der in ihm enthaltenenObjekte (Geraden, Kreise, Polytope, usw.) folgende Fragestellunguntersucht („Erlanger Programm“, Felix Klein 1872):Welche Eigenschaften des Raumes (und der in ihm enthaltenenObjekte) bleiben erhalten (sind invariant), wenn man auf ihn einegegebene Gruppe von umkehrbar eindeutigen Abbildungen ausübt?Es ergibt sich folgende (nicht vollständige) Unterteilung:Teilgebiet derAbbildungsgeometrie(Theorie)KongruenzgeometrieGruppe der betrachtetenAbbildungen(Transformationsgruppe)Kongruenzabbildungen,z.B. Spiegelung,Verschiebung, DrehungÄhnlichkeitsgeometrie Ähnlichkeitsabbildungen,z.B. zentrischeStreckungTopologietopologische (= stetige)Abbildungen,genauer: umkehrbareindeutig und bistetigInvarianzenmetrische Eigenschaftenwie Längen,Flächen- und RauminhalteGeraden-/Kreistreue,Parallelität, Winkeltreue,Längenverhältnisseoffen/geschlossen(Kurven),zusammenhängend/nicht zusammenhängend(Gebiete)innen/außen(Gebiete)Schnitt (Kurven)Jede Theorie enthält zusätzlich alle Invarianzen der darunterstehendenTheorien! Also nimmt von oben nach unten die „Figurentreue“ab, d.h. es bleiben immer weniger Eigenschaften einer geometrischenFigur erhalten.Wichtig: Figuren, die sich im jeweiligen Teilgebiet durch eineAbbildung der entsprechenden Transformationsgruppe ineinanderüberführen lassen, gelten als identisch (d.h. ununterscheidbar imSinne der Theorie).

Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der GrundschuleGrundlagen und Ziele• Piaget: Im Laufe der kindlichen Entwicklung bei derWahrnehmung und Wiedergabe von Figuren werdenzuallererst (schon in der präoperationalen Phase, ca. 3,5-4 J.)topologische Invarianzen beherrscht (Bsp.: Ein Quadrat wirdals geschlossene Kurve wiedergegeben.).• handelnder Zugang möglich (Schnüre, Gummizüge, Drahtetc.)• zeichnerische Behandlung topologischer Fragestellungenerfordert wenig Präzision• Verbindung zum Alltag: z.B. S-Bahn-Netz als topologischesNetz• spielerischer und kreativer (und dennoch zielgerichteter)Umgang mit anspruchsvollen kombinatorischenFragestellungen• offener und/oder problemorientierter Unterricht (Algorithmen –also „Rezepte“ – spielen kaum eine Rolle)

Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der Grundschule1. Kurvena) Unterscheidung zwischen offenen und geschlossenen Kurven• geschlossen heißt: alle Perlen an der Schnur können in beideRichtungen bewegt werden, alle Punkte können Anfangs- undEndpunkt sein.b) Unterscheidung zwischen einfachen und nicht einfachen Kurven(ohne/mit Selbstüberschneidungen bzw. Doppelpunkten)• Abhängigkeit der Anzahl der Gebiete von der Anzahl derDoppelpunkte• Zeichnen/Vervollständigen von Kurven nach VorgabeAnwesenheitsaufgabe:Wie viele verschiedene geschlossene nicht-einfache Kurven mitzwei Doppelpunkten gibt es?Grundschulformulierung: Wie viele geschlossene Eisenbahnlinienmit zwei Kreuzungen gibt es?

Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der Grundschule2. Gebiete• Wie wird die Ebene durch ein Netz von Kurven zerlegt?• In der Ebene gilt der Jordansche Kurvensatz: Einegeschlossene Kurve teilt die Ebene in zwei Bereiche (also z.B.Inneres und Äußeres: „Die Maus ist gefangen!“). Also kanndurch Ausmalen festgestellt werden, ob eine unübersichtlichekomplizierte Kurve geschlossen ist.• Anmerkung: Dieser Satz gilt auch auf der Kugeloberfläche(Problem: Inneres/Äußeres), aber nicht auf dem Torus(Schwimmring)!• Färbeprobleme: Ausmalen von Gebieten (BenachbarteGebiete dürfen nicht gleich gefärbt sein!); „Wie viele Farbenbrauchst Du?“ (Vierfarbensatz, erst 1976 durch Computerhilfebewiesen!)• Zerlegungsprobleme, Zusammenhang mit Logik

Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der Grundschule3. Netze (Graphen)• Netz (Graph): Figur aus Ecken (Knoten, Punkte) und Kanten(Bögen), bei der jede Kante an einer Ecke beginnt und aneiner Ecke endet. Eine Kante mit identischem Anfangs- undEndpunkt heißt Schleife. Die Anzahl der Kanten einer Eckeheißt Ordnung der Ecke.• Euler-Weg (unikursale Kurve): Weg durch alle Ecken, der jedeKante genau einmal durchläuft. Ein geschlossener Euler-Wegheißt Euler-Kreis.• Welche Netze ermöglichen einen Euler-Weg/Euler-Kreis (vgl.Wäschetrockenplatz, „Haus des Nikolaus“, KönigsbergerBrückenproblem)?• Ein Baum ist ein zusammenhängendes Netz ohne Rundweg.Für einen Baum mit e Ecken und k Kanten gilt: e=k+1.• Charakteristik eines Netzes N mit e Ecken, k Kanten, das dieEbene in f Gebiete unterteilt: C(N):=e−k+f. Es gilt: C(N)=2 füralle zusammenhängenden Netze N. [Manchmal wird der Satzformuliert als C(N)=1; dann wird das äußere Gebiet nichtmitgezählt!]Beweis (anschaulich): Wenn das äußere Gebiet unter Wassersteht, muss man k d geeignete Kanten durchtrennen, um f–1innere Flächen zu fluten (also k d =f–1). Am Ende bleibt einBaum mit k r Kanten übrig: e=k r +1. Zusammen mit k=k d +k r folgtdie Behauptung.

Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der GrundschuleEulersche PolyederformelKörperWürfel(Hexaeder)Tetraeder(Vierflach)Prisma(z.B. Haus)FußballAnzahlEcken (e)AnzahlKanten (k)AnzahlFlächen (f)e+f k+2Oktaeder(Achtflach)Dodekaeder(Zwölfflach)Ikosaeder(Zwanzigflach)Es gilt der folgende Satz (EULERscher Polyedersatz):Für ein konvexes Polyeder oder ein Polyeder, das sich durch stetigeDeformation in ein konvexes Polyeder deformieren lässt, gilt für dieAnzahl e der Ecken, die Anzahl k der Kanten und die Anzahl f derFlächen:e − k+f=2

Pädagogische Hochschule Ludwigsburg – Institut für Mathematik und InformatikGeometrie (Mohr)Topologie in der GrundschuleDie fünf platonischen Körper ...TetraederWürfelOktaeder Dodekaeder Ikosaeder... und ein Beispiel für einen archimedischen Körper:FußballFußball als Polyeder(begrenzt von 12 Fünfeckenund 20 Sechsecken)