Wiederholungs-Klausur am Freitag 30. Januar 2004 - Mohr.lehrer ...

1Prof. S. Krauter Semesterklausuren – Geometrie Sem_Klsr_Geo.docWiederholungs-Klausur am Freitag 30. Januar 2004Bitte füllen Sie die persönlichen Angaben auf diesem Blatt in Druckschrift aus undgeben Sie das Blatt in Ihrem Doppelbogen mit ab.Persönliche Angaben:Name Vorname Matr.-Nr. Sem. im SS-03Klausurergebnis:A1 40 P A2 15 P A3 12 P A4 15 P40 min 15 min 15 min 15 mina) 10 b) 4 c) 4 d) 4 e) 6 f) 6 g) 6 Z1: 5 Z2: 5 Z3: 5 12 Z: 3 B: 12Klausurpunkte: Übungspunkte: Gesamt:Zugelassene Hilfsmittel:‣ Ein nicht programmierbarer Taschenrechner.‣ Schreib- und Zeichenwerkzeug.‣ 1 namentlich gekennzeichnetes Blatt DIN-A4 mit eigenen Notizen.Die Lösungen sind sauber und vollständig auf kariertem Doppelbogen DIN A 4mit üblichem Kopf und Rand darzustellen. Die Form wird mit bewertet.Konstruktionen sind sauber und genau mit dünnem Bleistiftstrich auszuführen.Alle Lösungen sind knapp, aber hinreichend zu begründen.Arbeitszeit: 90 Minuten.Die durch Abgabeblätter erworbenen Punkte werden addiert.Die Klausur ist bestanden, falls insgesamt mindestens 40 Punkte erworben werden.Eine Klausur mit weniger als 24 Punkten kann nicht gewertet werden.

2Aufgabe 1:FirstEin Haus ist b = 6 m breit, a = 10 m lang und vomBoden bis zum Trauf h 1 = 5 m hoch. Das Haus hat ein GratWalmdach, das an allen vier Dachflächen die gleicheDachneigung von α = 60° zur horizontalen Ebene hat.Traufa) Zeichnen Sie das Haus in DreitafelprojektionTrauf(Grundriss, Aufriss, Seitenriss) in zugeordneterLage im Maßstab 1:100.Platzbedarf: 11 cm oben; 8 cm unten, 12 cm rechts; 7 cm linksb) Bestimmen Sie aus der Zeichnung die Höhe h 2 des Firstes über der Traufhöhe(und damit die Höhe des Hauses h = h 1 + h 2 ) sowie die Länge f des Firstes.c) Bestimmen Sie durch Ausklappen einer Dachfläche im Grundriss die wahre Größedieser Dachfläche und die Länge g der Dachgrate.d) Bestimmen Sie durch Zeichnung den Winkel ϕ, den der Grat mit dem horizontalenDachboden bildet. Ist er größer oder kleiner als die Dachneigung α?e) Berechnen Sie die Höhe h 2 und die Firstlänge f.f) Berechnen Sie die gesamte Dachfläche des Hauses.g) Berechnen Sie den „umbauten Raum“ d.h. das Volumen des Hauses.Aufgabe 2: (Konstruktion bitte auf vorgegebenem Beiblatt durchführen)Ein Indianer will von seinem Standort A zu seinem Zelt Z. Dabei durchschwimmt erden Fluss f mit den parallelen Ufern p und q genau senkrecht zum Ufer, geht dann zumBach b und watet dort eine Strecke der Länge s um seine Spur zu verwischen. VomBach geht er dann direkt nach Z. Geben Sie unter diesen Nebenbedingungen denkürzesten Weg des Indianers von A nach Z an. Erläutern Sie kurz Ihre Konstruktion.Aufgabe 3:Gegeben ist ein rechtwinklig-gleichschenkliges Dreieck ABC mit der Seitenlänge AB =8 cm und dem Winkel γ = ∠ ACB = 90°. Die Seitengeraden dieses Dreiecks seien mitAB = c, BC = a und CA = b bezeichnet, die Spiegelungen an ihnen mit a, b bzw. c.Zeichnen Sie das Dreieck ABC. Bestimmen Sie die Art und die Kenndaten derAbbildung ϕ = a b c b c a . (Reihenfolge von links). Erläutern Sie Ihre Konstruktion.Aufgabe 4:Beweisen Sie einen der folgenden Sätze:(Zur Zeichnung: a=13, b=10, c=12).a) Spiegelt man den Höhenschnittpunkt H eines Dreiecks am Mittelpunkt M einerDreiecksseite, so liegt dieser Spiegelpunkt H’ auf dem Umkreis k des Dreiecks.b) Die Höhen eines Dreiecks sind die Winkelhalbierenden im Höhenfußpunktedreieck.Hinweis: Benützen Sie z.B. die Thaleskreise über AH und BH.

3sApqb

510,2 cm60 °60 °5 cm6,01 cm6,71 cm10 cm4 cm6,01 cm5,2 cm50,77 °6,71 cm

6Aufgabe 2:Man spiegeltszunächst Z an b zuAZ 1 .Dann nimmt man dieA2pA1Watestrecke derVqLänge s parallel zu bweg und erhält Z 2 .Danach nimmt manWnoch die Querungdes Flusses f wegZund erhält Z 3 .Die kürzestebVerbindung von AXnach Z 3 ist dieYgeradlinigeVerbindungsstrecke.Z3In diese wird nunjeweils die Querungund die WatestreckeZ2Z1eingebaut und man erhält den Streckenzug A-V-W-X-Y-Z als kürzeste Verbindung unterden genannten Bedingungen.Zeichnung siehe gesondertes Blatt.Aufgabe 3:Ea b c b c a= a (b c) (b c) aCe= a (b c)² a= a A a= a C e= b e= EbABca

8Bitte füllen Sie die persönlichen Angaben auf diesem Blatt in Druckschrift aus und gebenSie das Blatt in Ihrem Doppelbogen mit ab.Persönliche Angaben:Name Vorname Matr.-Nr. Sem. im WS 01-02Klausurergebnis:Aufg. 1 20PAufg. 2 14PAufg. 3 16PAufg. 4 14PAufg. 520 min 15 min 15 min 15 min 25 mina) 2 b) 10 c)8a) 4 b) 10 a) 8 b) 8 Z: 2 B: 12 a) 10 b) 1424 PKlausurpunkte: Übungspunkte: Gesamt:Zugelassene Hilfsmittel:Eine Doppelseite (1 DIN-A4-Blatt) mit handschriftlichen Notizen mit Namen undMatrikelnummer versehen.Ein nicht programmierbarer Taschenrechner. Schreib- und Zeichenwerkzeug.Die Lösungen sind sauber und vollständig auf kariertem Doppelbogen DIN A 4darzustellen. Die Form wird mit bewertet.Zeichnen Sie bitte sorgfältig, sauber und genau! Dies wird bewertet.Arbeitszeit: 90 Minuten. Erreichbare Punktzahl: 80. Anrechnung aus Übungen: 6+6.Die Klausur ist bestanden, falls insgesamt mindestens 40 Punkte erworben werden.Eine Klausur mit weniger als 24 Punkten kann nicht gewertet werden.Aufgabe 1:a) Ergänzen Sie zu einem wahren Satz:„Das Produkt von drei Geradenspiegelungen ist genau dann wieder eineGeradenspiegelung, wenn .....“b) Beweisen Sie den Satz aus a).c) Gegeben sind drei Geraden a, b und c (siehe Beiblatt!).Bestimmen Sie Art und Kenndaten (z.B. Drehpunkt und Drehwinkel einer Drehung) derAbbildung α = a b c , die sich als Produkt der drei Geradenspiegelungen ergibt(Reihenfolge von links nach rechts, d.h. die Spiegelung a an der Gerade a zuerst).Aufgabe 2:

9a) Von einem Fünfeck ABCDE sind die Seitenmitten P, Q, R, S und T gegeben (P Mittevon AB, Q Mitte von BC, usf.). Benützen Sie das Beiblatt.Konstruieren Sie Fünfeck ABCD zu den gegebenen Punkten P, Q, R, S und T.b) Analysieren Sie die Lösbarkeit der Aufgabe für ein beliebiges n-Eck (n≥3).Aufgabe 3:Gegeben sind die zum Dreieck ABC kongruenten Dreiecke PQR und XYZ (sieheBeiblatt).Bestimmen Sie die Art und die Kenndaten derjenigen Kongruenzabbildungen α bzw.β, die das Dreieck ABC in das Dreieck PQR bzw. in XYZ abbilden.Begründen Sie Ihre Antworten und Konstruktionen kurz aber vollständig.Aufgabe 4:In einem Sehnenviereck sind die Diagonalen zueinander senkrecht.Konstruieren Sie ein solches Viereck.Zeigen Sie, dass die Verbindungsgerade der Mitte einer Seite mit demDiagonalenschnittpunkt S senkrecht auf die Gegenseite trifft.Hinweis: Beachten Sie, dass der Diagonalenschnittpunkt S auf dem Thaleskreis übereiner Vierecksseite liegt.Aufgabe 5:Zu beiden Teilaufgaben sind jeweils sämtliche Lösungen zu ermitteln.Die Konstruktion ist kurz zu erläutern.Machen Sie jeweils allgemeine Aussagen über die Lösbarkeit und möglicheLösungsanzahl der Aufgabe bei beliebigen Vorgaben.a) Gegeben sind zwei sich nicht schneidende Kreise k 1 und k 2 sowie eine Strecke AB.Gesucht sind alle Strecken PQ mit P∈k 1 und Q∈k 2 , wobei die Strecke PQ zu ABparallel und gleich lang ist. Konstruieren Sie die sämtlichen Lösungen.b) Gegeben ist ein Kreis k, ein Punkt P außerhalb (oder innerhalb) des Kreises k und eineStreckenlänge s.Gesucht sind Sekanten durch P, auf denen k eine Sehne der gegebenen Länge sausschneidet.

10Name:.................................................................................W-Klausur Elementargeometrie; 02/2002Zu Aufgabe 1 c)Matr.-Nr...........................BacCbAZu Aufgabe 2:SRTQP

11Name:.................................................................................W-Klausur Elementargeometrie; 02/2002Zu Aufgabe 3:Matr.-Nr...........................YZXRQCPABZu Aufgabe 5 b):skMP

Lösungen zur Wiederholerklausur Elementargeometrie vom 1. Februar 2002:Lösung zu Aufgabe 1:a) „... wenn die drei Geraden in einem (Parallel- oder einem Punkt-) Büschel liegen.“b) (i) Gegeben sei ein Punkt- oder Parallelbüschel a, b, c. Dann kann man das Produkt ab so durch a‘b‘ ersetzen, dass b‘ = c ist, denn im ersten Fall gehen alle drei durcheinen Punkt und im zweiten Fall sind alle drei parallel. Also ist a b c = a‘.(ii) Sei a b c = d. Daraus folgt a b = d c.Fall1: a b ist eine Drehung. Dann ist d c dieselbe Drehung, d.h. c muss durch denSchnittpunkt von a und b verlaufen. Die Geraden a, b und c bilden ein Punktbüschel.Fall2: a b ist eine Translation. Dann ist d c dieselbe Translation, d.h. c muss zu aund b parallel sein. Die Geraden a, b und c bilden also ein Parallelbüschel.c) a b c = a‘ b‘ c mit b‘⊥c und ∠(a, b) = ∠(a‘, b‘)= a‘ b‘‘ c‘‘ mit b‘‘⊥a‘ und ∠(b‘, c) = ∠(b‘‘, c‘‘) = 90°.Damit haben wir insgesamt a‘⊥b‘‘⊥c‘‘ also a‘⏐⏐c‘‘. Daher ist a’b‘‘c‘‘ = a’c‘‘b‘‘ = b‘‘a’c‘‘eine Gleitspiegelung mit der Gleitachse b‘‘ und dem Schubvektor v = 2*dist(a‘,c‘‘).12Lösung zu Aufgabe 2:b) Wir analysieren die Aufgabe zunächst für ein beliebiges n-Eck:P Q RA B C ... AA ist Fixpunkt der Abbildung α = P Q R ... , die das Produkt von nPunktspiegelungen an den n Seitenmitten ist.Fall 1: n ist ungerade. Dann ist α eine Punktspiegelung. Diese hat genau einenFixpunkt. Daher ist in diesem Fall die Aufgabe stets eindeutig lösbar.Fall 2: n ist gerade. Dann ist α eine Translation.Ist α eine echte Translation, so gibt es keinen Fixpunkt und die Aufgabe ist unlösbar.Ist α jedoch die Identität, so kann jeder Punkt der Ebene als Eckpunkt A dienen.a) Im Falle n=5 ergibt sich die Lösung eindeutig durch A = P Q R S T. Das Produktvon drei Punktspiegelungen ist die Punktspiegelung am viertenParallelogrammpunkt: (P Q R) S T = U S T = V = A.Lösung zu Aufgabe 3:b) Das Bilddreieck YXZ ist gegensinnig kongruent zu ABC. Dabei sind dieMittelsenkrechten entsprechender Punkte nicht identisch, also muss es sich bei derAbbildung um eine Gleitspiegelung handeln, da eine Achsenspiegelung nicht in Fragekommt und es andere gegensinnige Kongruenzen nicht gibt. Man erhält dieGleitachse g durch Halbierung der Strecken AY, BX und CZ. Damit kann man dasZwischenbild nach der Spiegelung und auch den Schiebevektor v bestimmen.

c) Das Bilddreieck QRP ist gleichsinnig kongruent zu ABC. Da entsprechende Streckennicht zueinander parallel liegen, kann es sich nicht um eine Verschiebung handeln.Folglich kommt nur eine Drehung in Frage, andere gleichsinnige Kongruenzen gibt esnicht. Man erhält den Drehpunkt D als Schnittpunkt der Mittelsenkrechten derVerbindungsstrecken entsprechender Punkte. Der Drehwinkel ϕ ergibt sich alsWinkel zwischen zwei entsprechenden Strecken.13Lösung zu Aufgabe 4:DC90 °W(DSM1) = W(BSP) weil ScheitelwinkelW(M1SA) + W(DSM1) = 90° n. VoraussetzungW(SAM1) = W(M1SA) weil ASM1 gleichschenkligW(SAM1) = W(CBS) Umfangswinkel über DC.Folglich: W(SPB) = 180 - W(BSP) - W(PBS) = 90°.M1SMPABLösung zu Aufgabe 5:a) Q liegt erstens auf dem Kreis k2 und fernerauf dem Bild k1‘ von k1 bei derVerschiebungmit dem Vektor AB .AB k2Man erhält 2 Lösungen.P1Q1Es gibt entweder keine, eine oder zweik1Lösungen, je nachdem sich k2 und k1‘meiden, berühren oder schneiden.b) Wir wählen A beliebig auf k.M1M1'Nun verschieben wir A um s nach A‘.Der Kreis um A mit Radius sP2Q2schneidet aus dem Kreis k SehnensT2AS‘ der Länge s aus.kNun nützen wir die Rotationssymmetriedes Kreises k aus, d.h. wir drehen PS2um M, bis es bei P‘ auf AS‘ liegt.MDer Kreis um M durch P schneidet diePGerade AS‘ in P‘. Damit haben wirS1eine Sekante g‘, die aus k eine Sehne derT1gewünschten Länge s ausschneidet.S'Da diese Sekante nicht durch P geht,drehen wir sie zurück um M bis P‘ in P übergeht.P'Damit haben wir die Lösung g und erhalten einezweite Lösung g‘ durch Spiegeln an PM.Für sd keine Lösung.M2k1'As'

14Klausur am Freitag 17. Oktober 2003Bitte füllen Sie die persönlichen Angaben auf diesem Blatt in Druckschrift aus und gebenSie das Blatt in Ihrem Doppelbogen mit ab.Persönliche Angaben:Name Vorname Matr.-Nr. Sem. im SS-03Klausurergebnis:A130 PA3 24PA222 P35 min 25 min 20 min 10 mina) 10 b) 6 c) 8 d)6a) 12 b)12a) 8 b) 8 c)6A41212 PKlausurpunkte: Übungspunkte: Gesamt:Zugelassene Hilfsmittel:‣ Ein nicht programmierbarer Taschenrechner.‣ Schreib- und Zeichenwerkzeug.‣ 1 namentlich gekennzeichnetes Blatt DIN-A4 mit eigenen Notizen.Die Lösungen sind sauber und vollständig auf kariertem Doppelbogen DIN A 4 mitüblichem Kopf und Rand darzustellen. Die Form wird mit bewertet.Konstruktionen sind sauber und genau mit dünnem Bleistiftstrich auszuführen.Alle Lösungen sind knapp, aber hinreichend zu begründen.Arbeitszeit: 90 Minuten.Die durch Abgabeblätter erworbenen Punkte werden addiert.Die Klausur ist bestanden, falls insgesamt mindestens 40 Punkte erworben werden.Eine Klausur mit weniger als 24 Punkten kann nicht gewertet werden.

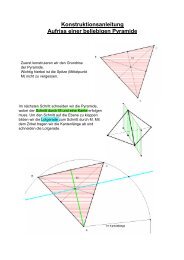
15Aufgabe 1:Ein gleichseitiges Dreieck hat die Höhe h 1 = 4,5 * 3 cm ≈ 7,8 cm (zur Zeichnung).Dieses gleichseitige Dreieck ist die Grundfläche einer Dreieckspyramide.Die Pyramide hat gleichlange zur Spitze laufende Seitenkanten der Länge s = 10 cm.a) Zeichnen Sie die Pyramide in Grund- und Aufriss.Wählen Sie selbst eine geeignete Lage. Beschreiben Sie kurz Ihre Konstruktion.b) Zeichnen Sie ein Schrägbild der Pyramide mit der in a) gewählten Lage.Entscheiden Sie sich dabei für eine der Varianten Frontschau oder Vogelschau.c) Bestimmen Sie die Grundkante a, die Körperhöhe k der Pyramide sowie die Höheh 2 der Seitendreiecke durch Konstruktion und Rechnung.d) Berechnen Sie die Oberflächengröße und den Rauminhalt der Pyramide.Aufgabe 2:a) Gegeben ist das Viereck A(0 ; 0) B(16; 0) , C(16 ; 6) , D(4; 14).Konstruieren Sie zu diesem Viereck den Ecken- und den Flächenschwerpunkt.Begründen Sie Ihre Konstruktion.Hinweis: Die Eigenschaften von Dreiecksschwerpunkten dürfen als bekanntvorausgesetzt werden.b) Beweisen Sie:Die Winkelhalbierenden jedes beliebigen Vierecks bilden stets ein Sehnenviereck.Aufgabe 3:a) Welche Dreiecke bzw. welche Vierecke sind punktsymmetrisch? Begründungen!b) Ein n-Eck f ist punktsymmetrisch.Geben Sie möglichst viele Eigenschaften der n-Ecks-Figur f an. Begründungen!c) Zeichnen Sie ein punktsymmetrisches, aber nicht regelmäßiges, Sechseck.Aufgabe 4 A (alternativ zur Aufgabe 4B):Zur Zeichnung bitte Beiblatt verwenden!Ein Indianer will von seinem Standpunkt J auf kürzestem Weg zu seinem Zelt Zgelangen. Um seine Spur zu verwischen, watet er im Bach b eine Strecke von dergegebenen Länge s. Den breiten Strom mit den zueinander parallelen Ufern c und ddurchschwimmt er auf kürzestem Weg. Konstruieren Sie den Weg des Indianers.Aufgabe 4 B (alternativ zur Aufgabe 4A):Ein Rechteck ABCD hat die Seitenlängen AB = 5 cm und BC = 3 cm.Zeichnen Sie das Rechteck. Spiegeln Sie das Dreieck ABC zuerst am Punkt D nachA’B’C’ und dieses dann an der Diagonale AC nach A’’B’’C’’.Ermitteln Sie Art und Kenndaten der Abbildung, die ABC direkt in A’’B’’C’’ abbildet.Begründen Sie Ihre Ergebnisse.

16sJbBachcStromdZ

17Lösungen zu M2-Klsr-Okt-03:Aufgabe 1:a) Man zeichnet im Grundriss die Dreieckshöhe A’D’ = 7,8 cm in wahrer Länge.Senkrechte zu A’D’ in D’. Winkel 30° an A’D’ in A’. Dessen Schenkel schneidet dieSenkrechte im Punkt C’. Man erhält leicht B’.Durch Ausklappen des Seitendreiecks mit der Schenkellänge s = 10 cm erhält mandas Seitendreieck und dessen Höhe h 2 = 8,93 cm.Durch Übertrag der Strecke A’B’ in den Aufriss (Ordnerlinien) erhält man A’’B’’ inwahrer Länge. S’’ erhält man als Schnitt der beiden Kreise um A’’ mit Radius s undum B’’ mit Radius h 2 . Das Dreieck A’’S’’B’’ ist parallel zur Aufrissebene und wird inwahrer Größe abgebildet. Damit ergibt sich die Körperhöhe zu 8,54 cm.Zeichnungen siehe nächste Seite.b) Zeichnungen siehe nächste Seite (verkleinert).Dort sind die beiden möglichen Schrägbilder jeweils• über dem Grundriss (Vogelschau oder Militärprojektion mit Verzerrungswinkel 90°und Verkürzung 1) bzw.• über dem Aufriss (Frontschau oder Kavalierprojektion mit Verzerrungswinkel 45°und Verkürzung 0,5) konstruiert.c) Im gleichseitigen Dreieck zerlegt die Höhe das Dreieck in zwei rechtwinklige Dreiecke.Damit kann man aus der Seitenlänge nach Pythagoras die Höhe berechnen und erhältah 1 = * 3 . Aus der Vorgabe h 1 = 4,5 * 3 ergibt sich daher die2Grundkante a = 9 cm.Die Seitenhöhe erhält man nach Pythagoras aus dem umgeklappten Seitendreieck:2⎛ a ⎞h 2 ² = s² - ⎜ ⎟⎠ = 100 – 4,5² = 79,75 und damit die Seitenhöhe h 2 = 8,930 cm.⎝ 2Die Körperhöhe erhält man nach Pythagoras aus dem Aufriss:P’’A’’ hat nach dem Schwerpunktssatz für Dreiecke die Länge 2/3 * h 1 = 3* 3 .Damit gilt für das rechtwinklige Dreieck A’’P’’S’’: k² = s² - (P’’A’’)² = 100 – 27 = 73.Damit erhält man die Körperhöhe k =73 cm = 8,544 cm.d) Oberflächengröße = Grunddreieck + 3 * Seitendreieck=(0,5 * 9 * 4,5 * 3 + 3 * 0,5 * 9 * 79 , 75 ) cm²= ( 35,074 + 3 * 40,186) cm² = 155,6 cm².Rauminhalt = 1/3 * G * k = 1/3 * 35,074 * 8,544 = 99,89 cm³.

Aufgabe 1:Grund- und Aufriss;Konstruktion dergesuchten Längen.188,54 cm7,8 cm9,01 cm8,93 cm10 cm

19Aufgabe 1 b):Frontschau mit a = 45° und k = 0,5.Aufgabe 1 b):Vogelschau mit a = 90° und k=18,54 cm90 °45 °9 cm3,9 cm

20Aufgabe 1; Tetraeder in Grund- und Aufriss10 cm8,93 cm8,54 cm9 cm8,93 cm8,54 cm

21Aufgabe 1: Frontschau(Kavalierprojektion)Vogelschau(Militärprojektion):8,54 cm10 cm7,8 cm8,93 cm9 cm

22Aufgabe 2:a) Eckenschwerpunkt:Man fasst je zwei Ecken z.B. A und B sowie C und D zusammen. Ihr gemeinsamerSchwerpunkt liegt jeweils in ihrem Mittelpunkt. Der Mittelpunkt zwischen diesen beidenSeitenmitten ist Eckenschwerpunkt SE (9;5). Er ist der Mittelpunkt desMittenparallelogramms des Vierecks ABCD.Flächenschwerpunkt:Man zerlegt das Viereck ABCD durch die Diagonale AC in zwei Teildreiecke ABC undACD, deren Schwerpunkte S 1 und S 2 man in der üblichen Weise erhält (Schnittpunktder Seitenhalbierenden). Der gemeinsam Schwerpunkt dieser beiden Dreiecke mussauf der Verbindungsstrecke S 1 S 2 liegen.Analog geht man vor mit der Diagonale BD und erhält die Dreiecksschwerpunkte S 3und S 4 . Der Flächenschwerpunkt S des Vierecks ist der Schnittpunkt von S 1 S 2 mitS 3 S 4 . Man erhält den Flächenschwerpunkt SF(8; 5,2).DS2S4S3SFSECS1AB

23b) Winkelhalbierendenviereck in einem beliebigen Viereck:Nach Konstruktion der Winkelhalbierenden erhält man für die Winkel imWinkelhalbierendenviereck PQRS bzw. für ihre jeweiligen Scheitelwinkel die Größen180°- ½ * (α + δ) bei R, 180° - ½ * (β + γ) bei P,180° - ½ * (γ + δ) bei S und 180° - ½ * (α + β) bei Q.Die Summe der Gegenwinkel bei R und P ist also180°- ½ * (α + δ) + 180° - ½ * (β + γ) = 360° - ½ * (α+β+γ+δ) = 180°denn die Winkelsumme α+β+γ+δ = 360° gilt für jedes Viereck.Damit ist aber PQRS als Sehnenviereck nachgewiesen.D102 °QCRP78 °SABAufgabe 3:a) Es gibt kein punktsymmetrisches Dreieck.Sei nämlich A ein Eckpunkt des Dreiecks. Dann muss auch der Bildpunkt A’ bei derSpiegelung am Zentrum Z ein Eckpunkt sein. Dasselbe gilt für jeden weiteren EckpunktB, womit man bereits vier Ecken hätte. Nimmt man jedoch Z selbst zu A und A’ alsweiteren Eckpunkt, so liegen die drei Punkte kollinear und es entsteht kein Dreieck.Punktsymmetrische Vierecke haben parallele Gegenseiten sind also Parallelogramme.Da umgekehrt jedes Parallelogramm punktsymmetrisch ist, gilt:Genau die Parallelogramme sind die punktsymmetrischen Vierecke,b) Das n-Eck f hat gerade Eckenzahl, parallele und gleich lange Gegenseiten undgleichgroße Gegenwinkel. Das folgt sofort aus den verallgemeinerten Überlegungenaus a) und den Eigenschaften einer Punktspiegelung.

24c) Man wähle ein Zentrum Z.Dann wähle man drei Punkte A, B und Cund ihre Spiegelpunkte A’, B’, C’ an Z.Dann ist das Sechseck ABCA’B’C’ sicherpunktsymmetrisch und – außer bei großemZufall – nicht regelmäßig.In diesem Ausnahmefall verändere man z.B.A willkürlich.C'B'ZA'CABAufgabe 4 A:Konstruktion siehe Beiblatt:Man nimmt aus allen Wegen die gleichlange Brücke heraus, das führt von Z zu Z’.Weiter nimmt man aus allen Wegen die gleichlange Watestrecke heraus, das führt von Z’zu Z’’. Unter allen Wegen von J nach Z’’ ist die gerade Verbindung die kürzeste.In diese fügen wir schrittweise die Watestrecke und die Brücke wieder ein und haben soden kürzesten Weg von J nach Z unter den genannten Zusatzbedingungen konstruiert.

25Lösung zu Aufgabe 4 A:sJbYXcUdWZ'Z''Z

Aufgabe 4 B:B'A'DCC'hABsVgA''C''B''Erste Lösung:Die Konstruktion von A’B’C’ und A’’B’’C’’ ist klar.Die Dreiecke ABC und A’’B’’C’’ sind gegensinnig kongruent, es muss also eineSpiegelung oder eine Gleitspiegelung geben, die ABC in A’’B’’C’’ abbildet.Erste Lösung:Die Mittelpunkte der Strecken AA’’, BB’’ und CC’’ sind kollinear und ergeben dieGleitachse g. Spiegelt man daran Dreieck ABC so erhält man über das Zwischenbildden Schubvektor.Zweite Lösung:Man kann die Punktspiegelung an D darstellen durch ein Produkt zweierGeradenspiegelungen g und h mit zueinander senkrechten Geraden g und h. Dabeiwählen wir g senkrecht zu s = AC und damit h parallel zu s = AC. Dann erhält manfür die Verkettung:(g h) s = (g (h s) = g Vwobei V die Verschiebung senkrecht zu h um den doppelten orientierten Abstand von hzu s ist.

27Klausur am Freitag 19. Oktober 2001Bitte füllen Sie die persönlichen Angaben auf diesem Blatt in Druckschrif aus und gebenSie das Blatt in Ihrem Doppelbogen mit ab.Persönliche Angaben:Name Vorname Matr.-Nr. Sem. im SS 01Klausurergebnis:Aufg. 1 12 P Aufg. 2 38 P Aufg. 3 12 P Aufg. 414 PAufg. 5 12P10 min 45 min 15 min 15 min 10 min3 3 3 3 a) 12 b) 8 c) 6 d) 6 e) 4 f) 2 A: 3 D: 3 K: 6 V: 8 O: 6 WH: 6 NW: 6Klausurpunkte: Übungspunkte: Gesamt:Zugelassene Hilfsmittel:Eine Doppelseite (1 DIN-A4-Blatt) mit handschriftlichen Notizen mit Namen undMatrikelnummer versehen.Ein nicht programmierbarer Taschenrechner. Schreib- und Zeichenwerkzeug.Die Lösungen sind sauber und vollständig auf kariertem Doppelbogen DIN A 4darzustellen. Die Form wird mit bewertet.Zeichnen Sie bitte sorgfältig, sauber und genau! Dies wird bewertet.Arbeitszeit: 90 Minuten. Erreichbare Punktzahl: 80. Anrechnung aus Übungen: 6+6.Die Klausur ist bestanden, falls insgesamt mindestens 40 Punkte erworben werden.Eine Klausur mit weniger als 24 Punkten kann nicht gewertet werden.Aufgabe 1:Konstruieren Sie den kürzesten Weg des Indianers von A nach B unterBeachtung folgender Nebenbedingungen (siehe Beiblatt):1. Der Fluss muss senkrecht zu den beiden Uferlinien g und h überquertwerden.2. Im Bach f ist eine Watestrecke der Länge s = 4 cm zurückzulegen.Beschreiben und begründen Sie kurz Ihre Konstruktion.Bitte benützen Sie zur Zeichnung das vorgegebene Beiblatt.

28Aufgabe 2:Ein Schuppen ist 12 m lang, 6 m breit und bis zum Dachtrauf 5 m hoch.Die Höhe des Dachstuhls von der Traufhöhe bis zur Firsthöhe beträgt 4 m.Die vordere Giebelseite ist angewalmt (mit der gleichen Dachneigung wie dieSeitendächer). Am rückwärtigen Ende des Gebäudes befindet sich ein normaler Giebel.Quer zum Längsdach ist ein Querdach mit zwei normalen Giebeln aufgesetzt. DessenFirst verläuft in 7 m Abstand parallel zur Vorderseite des Langhauses (also in 5 mAbstand parallel zur hinteren Giebelseite des Langhauses). Die Dachneigung desQuerdaches ist die selbe wie beim Längsdach und der First des Querdachs verläuft aufgleicher Höhe wie der des Langhauses.a) Zeichnen Sie den Schuppen in Dreitafelprojektion im Maßstab 1:100 sauber,sorgfältig und genau auf das beiliegende Blatt.Wählen Sie die hintere Giebelseite des Schuppens parallel zur Aufrissebene (sieheBeiblatt).b) Zeichnen Sie ein Schrägbild des Schuppens (Frontschau; Zeichnung auf Beiblatt).Wählen Sie den Verzerrungswinkel zu 45° und das Verkürzungsverhältnis 0,5.c) Berechnen Sie die gesamte Dachfläche des Gebäudes.d) Berechnen Sie den umbauten Raum, d.h. das Volumen des Baukörpers.Hinweis: Für e) und f) können Sie die Zeichnung aus a) ergänzen.e) Bestimmen Sie die Länge der Dachkehle ( Zusammentreffen des Längsdaches mitdem Querdach) durch Zeichnung und Rechnung.f) Bestimmen Sie die Dachneigung durch Zeichnung und Rechnung.Aufgabe 3:Von den vier Seiten AB , BC , CD und DA eines Vierecks ABCD sind jeweils dieMittelsenkrechten a, b, c und d gegeben (siehe Beiblatt).a) Analysieren Sie dazu die Abbildungsfolge a b c d angewandt auf den Punkt A.Diskutieren Sie sämtliche Lösbarkeitsfälle für die gegebene Aufgabe (Determination).b) Konstruieren Sie das zugehörige Viereck ABCD.Verlangt ist eine saubere und genaue Zeichnung mit Begründung der Konstruktionsowie eine Angabe über die Lösbarkeit der Aufgabe im vorliegenden Fall.Aufgabe 4:Leiten Sie die Formeln für den Rauminhalt und die Oberfläche einer Kugel her.Formulieren Sie alle wesentlichen Sätze und Prinzipien, die Sie bei der Herleitungbenutzen.Aufgabe 5:Beweisen Sie: Die Winkelhalbierende eines Dreieckswinkels und seines Nebenwinkelsteilen die Gegenseite innen bzw. außen im Verhältnis der anliegenden Seiten.Hinweis: Benutzen Sie die Symmetrieeigenschaft der Winkelhalbierenden.Geeignet ist ein Dreieck mit den Seiten a = 3 cm, b = 6 cm und c = 4,5 cm.

Name:................................................................................................Matr.-Nr.....................................Elementargeometrie; 10/2001; zu Aufgabe 2.; Seitenriss AufrissGrundrissSchrägbild

Name:.......................................................................... Matr.-Nr.....................................Klausur Elementargeometrie; 10/2001.30Zu Aufgabe 1:AghBfZu Aufgabe 3:cadb

31Lösungen zur Klausur Elementargeometrie vom 19. Oktober 2001:Aufgabe 1:Jeder Weg enthält die Querung des Flusses PQ . Um diesen Vektor verschieben wirA nach A‘. Jeder Weg enthält die Watestrecke RS = s im Bach f. Um diesen Vektorverschieben wir A‘ nach A‘‘. Nun gilt es, den kürzesten Weg von A‘‘ nach B zu finden,der den Fluss f berührt. Dies gelingt mit Hilfe des Spiegelpunktes B‘ von B an f. DieVerbindung von A‘‘ mit B‘ liefert den Punkt, bei dem die Watestrecke in f endet. Damitkann der Weg rekonstruiert werden.Aufgabe 2:a) Im Grundriss sieht man den Hausumriss (Rechteck mit 6m x 12 m) in wahrerGröße, ebenso alle Traufkanten und die Firste.Im Aufriss erscheinen Traufhöhe (5 m) sowie Höhe des Dachstuhls über demTrauf (4 m) in wahrer Größe. Ebenso erscheint der First des Querhauses (6 m) inwahrer Größe. Das angewalmte Dachdreieck über der vorderen Giebelseiteerscheint nicht in wahrer Größe, weil es nicht parallel zur Aufrissebene liegt,sondern geneigt dazu.Im Seitenriss erscheint der Langfirst sowie der Giebel des Querhauses in wahrerGröße. Die Höhe des Dachdreiecks des Vordergiebels erscheint ebenfalls inwahrer Größe. Diese beträgt nach Pythagoras 5 m, denn die beiden Kathetenbetragen 3m (= halbe Hausbreite) und 4m (= Dachstuhlhöhe).b) Im Schrägbild werden alle zur Bildebene (= Aufrissebene) parallelen Stücke inwahrer Größe abgebildet (Hausbreite, Trauf- und Giebelhöhe, hinterer Giebel desLanghauses etc.). Alle dazu senkrechten Strecken werden unter dem Winkel 45°zueinander parallel abgebildet und auf halbe Länge verkürzt (k = 0,5).c) Dachfläche:Vorderes Giebeldreieck: A1 = ½ * 6m * 5m = 15 m².Zwei Parallelogramme am Längsdach: A2 = 2 * 4m * 5m = 40 m² (imSeitenriss ausgeklappt).Vier rechtwinklige Dreiecke am Querdach: A3 = 4 * ½ * 3m * 5m =30 m².Zwei Trapeze am hinteren Längsdach: A4 = 2 *2m + 5m2* 5m = 35 m².Damit erhält man die gesamte Dachfläche zuA = 120 m².Zusatzbemerkung:Das Dach steht über der gesamten Grundfläche des Hauses gleichgeneigt und zwar gemäß nebenstehender Skizze. Daher verhaltensich Grundfläche und Dachfläche wie 3 zu 5. Man erhält daher:Dachfläche = 5/3 * Grundfläche = 5/3 * 72 m² = 120 m².d) Umbauter Raum:Grundquader: V1 = 6m * 12m * 5m = 360 m³.Vordere Dachpyramide: V2 = 1/3 * 6m * 3m * 4m = 24 m³.435

32Langhausdachraum (Dreieckssäule 9m lang): V3 = ½ * 6m * 4m * 9m = 108 m³.Hinzu kommt der zusätzliche (!) Dachraum des Querhauses, bestehend aus zweiPyramiden mit dem Giebel als Grundfläche und der halben Hausbreite als Höhe:V4 = 2 * 1/3 * (1/2 * 6m * 4m) * 3m = 24 m³.Gesamtvolumen: V = 516 m³.Bemerkung: Es geht viel einfacher:Eine Hälfte des Querdachs entspricht genau dem vorne abgeschnittenenGiebelteil. Das Volumen ergibt sich also als Summe des Volumens vom normalenLanghaus plus ein Seitenteil des Querdaches:V = 12*(6*5+0,5*6*4) + 0,5*6*4*3/3 = 12*42 + 12 = 12 * 43 = 516 m³.e) Länge der Dachkanten: Die Giebelkanten haben die Länge 5 m (Pythagoras).Dachgrate bzw. Dachkehlen des Vorderdaches: d² = 3² + 5² = 34, damitd = 34 m ≈ 5,83 m.f) Dachneigung: tan α = 4/3 ⇒ α = 53,13°.Aufgabe 3:a) Wir analysieren folgendes Diagramm:a b c dA B C DAαDie Abbildung α = a b c d ist als Produkt von vier Geradenspiegelungen einegleichsinnige Kongruenz, also eine Drehung oder eine Translation. Der EckpunktA des möglichen Lösungsvierecks muss Fixpunkt dieser Abbildung α sein.(Vorsicht: Die Schlussfolgerung, dass α selbstinvers ist, ist nicht zulässig!!).• Ist α echte Translation so gibt es keinen Fixpunkt; in diesem Fall ist dieAufgabe daher unlösbar.• Ist α die Identität, so ist jeder Punkt Fixpunkt, also kann jeder Punkt derEbene als Eckpunkt A dienen und man erhält unendlich viele Lösungen.• Ist α dagegen eine echte Drehung, so gibt es genau einen Fixpunkt, dieserist dann einzige Lösung der Aufgabe.b) Im vorliegenden Fall konstruiert man wie folgt:Es sei P Schnittpunkt von a und b und Q Schnittpunkt von c und d.Dann ersetzt man ab durch a’b‘ mit b‘ = PQ und cd durch c’d‘ mit c‘ = PQ.Damit ergibt sich:a b c d = a‘ b‘ c‘ d‘ = a‘ b‘ b‘ d‘ = a‘ d‘ = Drehung(A; 2*∠(a‘, d‘)).

33Im vorliegenden Fall ergibt sich A als einzige Lösung.Man ergänzt zum Viereck ABCD durch fortlaufende Spiegelung von A an dengegebenen Mittelsenkrechten.Aufgabe 4:Zur Bestimmung des Volumens einer Kugel benutzt man das Prinzip von Cavalieri:Haben zwei Körper auf jeder Höhe x über der Grundfläche stets gleich großeQuerschnittsflächen, so sind sie volumengleich.hBegründung: V = ∫ qxdx ( ) .0Eine Halbkugel mit Radius r und ein Zylinder mit Radius r und Höhe r, aus dem vonoben ein Kegel mit Grundkreisradius r und Höhe r ausgebohrt ist, erfüllen dieVoraussetzungen des Satzes von Cavalieri, sie sind also volumengleich:Querschnitt bei der Halbkugel:HalbkugelZylinderq 1 (x) = π * q² = π* (r² - x²)qPzxryQuerschnitt beim ausgebohrten Zylinder:q 2 (x) = π * r² - π* x² = π* (r² - x²)x = y = zEs gilt also q 1 (x) = q 2 (x) für alle x, alsokann der Satz von Cavalieri angewendetwerden und beide Körper haben das gleicheVolumen.Man erhält daher das Volumen der Halbkugel zu:V HK = Zylindervolumen – Kegelvolumen = π * r³ - 1/3 * π * r³ = 2/3 * π * r³ .Damit ergibt sich das KugelvolumenDas Volumen eines Kegels beträgtDas Volumen eines Zylinders beträgtV = 34 * π * r³.V = 1/3 * Grundfläche * Höhe.V = Grundfläche * Höhe.Die Oberfläche einer Kugel erhält man durch folgende Überlegung:Man denkt sich die Kugeloberfläche aufgeteilt in eine Netz von sehr kleinen Zellen z.B. in Form eines Gradnetzes. Jede Zellenecke verbindet man mit demKugelmittelpunkt. Dann entstehen lauter kleine Pyramiden mit gekrümmterGrundfläche. Jede einzelne hat ein Volumen von V i = 1/3 * A i * r, wobei A i die Größeder Grundfläche ist. Dies stimmt umso genauer, je kleiner wir die Zellen wählen. DasGesamtvolumen der Kugel erhält man als Summe aller dieser Pyramidenvolumina: V

34= 1/3 * r * ∑ A i.iDie Summe aller A i ergibt aber gerade die Oberfläche O k der Kugel.Damit erhält man: V = 4/3 * π * r³ = 1/3 * r * O k und darausdie Formel für die Kugeloberfläche: O k = 4 * π * r².Aufgabe 5:Die Winkelhalbierende eines Winkels ist Symmetrieachse seiner beiden Schenkel.Man spiegelt das Dreieck ABC an der Winkelhalbierenden w des Winkels γ und ander Winkelhalbierenden w‘ seines Nebenwinkels und erhält die Punkte A‘, A‘‘, B‘und B‘‘. Nun sind folgende Strecken von gleicher Länge:CA = CA‘ = CA‘‘ = b CB = CB‘ = CB‘‘ = a.Außerdem sind die Strecken AA‘ und BB‘ zueinander parallel (beide senkrecht zu w)und ebenso die Strecken AA‘‘ und BB‘‘.Strahlensatz II mit Scheitel C ergibt: AA‘ : BB‘ = CA : CB‘ = b : a (1)Strahlensatz II mit innerem Scheitel D ergibt: AD : DB = AA‘ : BB‘ = b : a (2)Damit ist der Satz für die Winkelhalbierende bewiesen. Analog für den Nebenwinkel:Strahlensatz II mit innerem Scheitel C ergibt: AA‘‘ : BB‘‘ = CA : CB‘‘ = b : a (3)Strahlensatz II mit Scheitel E ergibt: AE : BE = AA‘‘ : BB‘‘ = b : a (4)Damit ist auch dieser Teil bewiesen.A''CB''B'AwDBw'EA'

35Korrektur- und Bewertungsvorschlag:Aufgabe 1:Vektor PQ von A nach A‘: 3P Vektor Watestrecke bei B oder A‘: 3P.Spiegelung von B an f nach B‘: 3P Begründung der Minimalität: 3P.Aufgabe 2:a) Grundriss, Aufriss und Seitenriss je 4 P: 12 Pb) Schrägbild: 8 P.c) Vier Teilflächen zu je 1,5 P 6 P.d) Vier Teilkörper zu je 1,5 P 5 P.e) Z und R je 2 P: 4 P.f) Z und R je 1 P: 2 P.Aufgabe 3:a) Analyse und Determination jeweils 3 P: 6 P.b) Konstruktion mit Text: 6 P.Aufgabe 4:Volumen: 8 P. (Cavalieri 3; Archimedes-Ansatz 3; Durchführung 2)Oberfläche: 6 P (Ansatz: 3; Durchführung 3).Aufgabe 5:Beweis in einem Fall: 8 P. Zusätzlich für den zweiten: 4 P.