- Page 2 and 3:
BIOINFORMATICS: Databases and Syste
- Page 4 and 5:
BIOINFORMATICS: Databases and Syste
- Page 6 and 7:
To Tish, Emily, Miles and Josephine
- Page 8 and 9:
TABLE OF CONTENTS INTRODUCTION ....
- Page 10 and 11:
INTRODUCTION Stanley Letovsky Bioin
- Page 12 and 13:
for wisdom. Where algorithms tend t
- Page 14 and 15:
gain performance by distributing qu
- Page 16 and 17:
systems described (OPM, BioKleisli,
- Page 18 and 19:
DATABASES
- Page 20 and 21:
1 NCBI: INTEGRATED DATA FOR MOLECUL
- Page 22 and 23:
figure 1, and all flows into the ID
- Page 24 and 25:
There are other sets of data that c
- Page 26 and 27:
2. Explicit declaration by the hist
- Page 28 and 29:
2. W. J. Wilbur, A retrieval system
- Page 30 and 31:
2 HOVERGEN: COMPARATIVE ANALYSIS OF
- Page 32 and 33:
Figure 1: Phylogenetic tree of the
- Page 34 and 35:
fragment. In some cases, a same gen
- Page 36 and 37:
Figure 2: Distribution of families
- Page 38 and 39:
the user can visualize all the anno
- Page 40 and 41:
Selecting orthologous genes with HO
- Page 42 and 43:
Thus, HOVERGEN allows one to do exh
- Page 44 and 45:
21. Saitou, N. Nei, M. The neighbor
- Page 46 and 47: 3 WIT/WIT2: METABOLIC RECONSTRUCTIO
- Page 48 and 49: protein sequence are used (e.g., OR
- Page 50 and 51: After we have accumulated an initia
- Page 52 and 53: Coordinating the Development of Met
- Page 54 and 55: Availability of the Pathways, Softw
- Page 56 and 57: 4 ECOCYC: THE RESOURCE AND THE LESS
- Page 58 and 59: epresented as an instance of the cl
- Page 60 and 61: The Gene--Reaction Schematic The ma
- Page 62 and 63: EcoCyc contains extensive informati
- Page 64 and 65: within compound windows uses a conc
- Page 66 and 67: Figure 4: The EcoCyc linear map bro
- Page 68 and 69: Figure 5: The software architecture
- Page 70 and 71: 6. Karp. Frame representation and r
- Page 72 and 73: Introduction 5 KEGG: FROM GENES TO
- Page 74 and 75: Binary relations Figure 1 : Level o
- Page 76 and 77: hierarchical text. The genome map i
- Page 78 and 79: (2) Java applets to search, compare
- Page 80 and 81: can be used for gene function assig
- Page 82 and 83: influenzae lacks the upper portion
- Page 84 and 85: Future Directions Figure 4. KEGG as
- Page 86 and 87: Introduction 6 OMIM: ONLINE MENDELI
- Page 88 and 89: The Entry Each OMIM entry is assign
- Page 90 and 91: Searching OMIM is as simple as typi
- Page 92 and 93: How OMIM is Curated OMIM is maintai
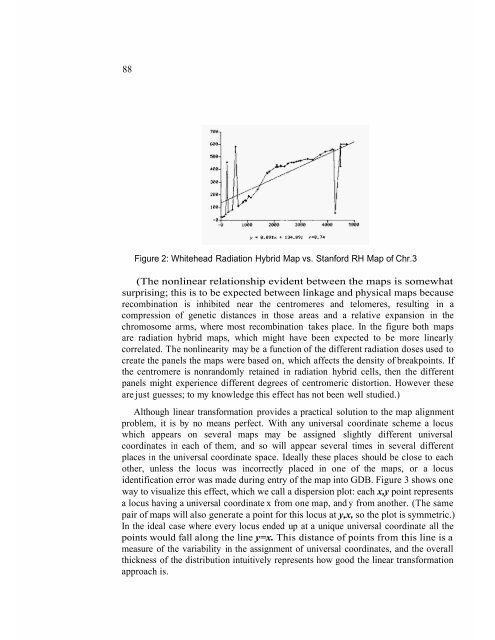
- Page 94 and 95: 7 GDB: INTEGRATING GENOMIC MAPS Int
- Page 98 and 99: Figure 3: Universal Coordinate Disp
- Page 100 and 101: Figure 5: Dispersion of linear (lef
- Page 102 and 103: which minimizes dispersion. The opt
- Page 104 and 105: Figure 10: A piece of an "comprehen
- Page 106 and 107: alignments are better for the speci
- Page 108 and 109: Summary 8 HGMD: THE HUMAN GENE MUTA
- Page 110 and 111: Data coverage and structure 101 By
- Page 112 and 113: Conclusions and Outlook 103 Being b
- Page 114 and 115: Introduction 9 SENSELAB: MODELING H
- Page 116 and 117: 107 For the purposes of the rest of
- Page 118 and 119: 109 users might advocate creating a
- Page 120 and 121: 111 The Associations table describe
- Page 122 and 123: Managing the Object Class Hierarchy
- Page 124 and 125: 115 In fig. 2, the Objects and Clas
- Page 126 and 127: 117 7. Mirsky JS, Nadkarni PM, Hine
- Page 128 and 129: 10 THE MOUSE GENOME DATABASE AND TH
- Page 130 and 131: genetics community fostered the ear
- Page 132 and 133: 123 Data acquisition for MGD includ
- Page 134 and 135: 125 In February 1998, a ‘cDNA and
- Page 136 and 137: Acknowledgments 127 MGD is funded b
- Page 138 and 139: 11 THE EDINBURGH MOUSE ATLAS: BASIC
- Page 140 and 141: expression database under developme
- Page 142 and 143: 133 For blastocysts the shape of th
- Page 144 and 145: 135 which is a cut at an arbitrary
- Page 146 and 147:
137 This defines a viewing directio
- Page 148 and 149:
139 plate spline [19] or polynomial
- Page 150 and 151:
12 FLYBASE: GENOMIC AND POST- GENOM
- Page 152 and 153:
143 Genes, including links via publ
- Page 154 and 155:
Public Access to FlyBase Data The c
- Page 156 and 157:
147 There are two classes of annota
- Page 158 and 159:
149 screens to identify direct or i
- Page 160 and 161:
13 MAIZEDB: THE MAIZE GENOME DATABA
- Page 162 and 163:
The bins map strategy has been empl
- Page 164 and 165:
Clicking on one of the orthologous
- Page 166 and 167:
* hyper-text linked to MaizeDB enti
- Page 168 and 169:
DISSEMINATION TO EXTERNAL DATABASES
- Page 170 and 171:
Appendix 2: part of the Query Form
- Page 172 and 173:
Introduction 14 AGIS: USING THE AGR
- Page 174 and 175:
Horn Fly--Haematobia Screwworm--Coc
- Page 176 and 177:
Figure 2 : Main AGIS Menu 167
- Page 178 and 179:
Figure 4 : Available Classes and Su
- Page 180 and 181:
Figure 6 : Query by Example and Que
- Page 182 and 183:
Figure 8 : Hypertext ACEDB Object a
- Page 184 and 185:
15 CGSC: THE E.COLI GENETIC STOCK C
- Page 186 and 187:
177 described once for that gene an
- Page 188 and 189:
FIGURE 1. A Query for an hsdR- recA
- Page 190 and 191:
FIGURE 2. A Query for a lacZ-(amber
- Page 192 and 193:
183 These are suggestions that dese
- Page 194 and 195:
SYSTEMS
- Page 196 and 197:
Introduction 16 OPM: OBJECT-PROTOCO
- Page 198 and 199:
189 OPM is a data model whose objec
- Page 200 and 201:
The OPM Database Development Tools
- Page 202 and 203:
ased on this query tree. Further qu
- Page 204 and 205:
195 Interface, except that one can
- Page 206 and 207:
197 Our strategy of providing suppo
- Page 208 and 209:
Acknowledgments 199 Between 1992 an
- Page 210 and 211:
Introduction 17 BIOKLEISLI:INTEGRAT
- Page 212 and 213:
203 In the remainder of this chapte
- Page 214 and 215:
pages : “4267-4274", abstract:
- Page 216 and 217:
BioKleisli in Action: Querying Biom
- Page 218 and 219:
209 savings in execution time is si
- Page 220 and 221:
References 211 13. NCBI ASN. 1 Spec
- Page 222 and 223:
Introduction 18 SRS: ANALYZING AND
- Page 224 and 225:
215 In SRS, databank structures are
- Page 226 and 227:
217 Operands also include named set
- Page 228 and 229:
Figure 1. The SRS Top Page. Figure
- Page 230 and 231:
Analyzing Data in SRS with Applicat
- Page 232 and 233:
223 other databanks, and define spe
- Page 234 and 235:
Figure 7. A SWISS-PROT entry with i
- Page 236 and 237:
Figure 8. The results of a query fo
- Page 238 and 239:
parser and documentation files, and
- Page 240 and 241:
23 1 12. Altschul, S.F., Gish, W.,
- Page 242 and 243:
Introduction 19 BIOLOGY WORKBENCH:
- Page 244 and 245:
Figure 1. Organization and Flow of
- Page 246 and 247:
237 In order to make wrapper develo
- Page 248 and 249:
the browser window containing a men
- Page 250 and 251:
either during the current Workbench
- Page 252 and 253:
PROFILESCAN Comparison of protein o
- Page 254 and 255:
20 EBI: CORBA AND THE EBI DATABASES
- Page 256 and 257:
247 the Object Request Broker (ORB)
- Page 258 and 259:
249 Every database entry is represe
- Page 260 and 261:
251 Wrappers with and without State
- Page 262 and 263:
Discussion 25 3 CORBA and IDL minim
- Page 264 and 265:
Introduction 21 BIOWIDGETS:REUSABLE
- Page 266 and 267:
Visualization Solutions 257 Turnkey
- Page 268 and 269:
259 The architecture also exploits
- Page 270 and 271:
possible because the bioWidget arch
- Page 272 and 273:
263 4. Gish, Warren (1994-1997). un
- Page 274 and 275:
22 ACEDB: THE ACE DATABASE MANAGER
- Page 276 and 277:
267 On the other hand, most users c
- Page 278 and 279:
269 Street, City and State into "ma
- Page 280 and 281:
27 1 to a running database after ed
- Page 282 and 283:
273 database the class Map refers t
- Page 284 and 285:
275 were waiting for the Biowidget
- Page 286 and 287:
277 table of 13 columns and 1 milli
- Page 288 and 289:
Introduction 23 LABBASE: DATA AND W
- Page 290 and 291:
28 1 We will use as a running examp
- Page 292 and 293:
LabBase Details 283 A LabBase objec
- Page 294 and 295:
When the procedure completes, LabFl
- Page 296 and 297:
287 sequence-assembly Worker in our
- Page 298 and 299:
289 The Worker converts the object
- Page 300 and 301:
291 Genome Research and are beginni
- Page 302 and 303:
INDEX
- Page 304 and 305:
INDEX A of Agricultural Genome Info
- Page 306 and 307:
of vertebrate genes, 21-33 developm
- Page 308 and 309:
GenBank database query software of,
- Page 310 and 311:
Metabolic Pathway Database, 38 Meta
- Page 312 and 313:
conversion to ‘gi’ identifiers