LR Rabiner and RW Schafer, June 3

More documents

Recommendations

Info

DRAFT: L. R. Rabiner and R. W. Schafer, June 3, 2009 468CHAPTER 8. THE CEPSTRUM AND HOMOMORPHIC SPEECH PROCESSING 4 2 0 −2 (a) Complex Cepstrum using Polynomial Roots −4 −150 −100 −50 0 50 100 150 0.5 0 −0.5 (b) Cepstrum using Polynomial Roots −150 −100 −50 0 Quefrency (Samples) 50 100 150 Figure 8.28: Cepstrum analysis based on polynomial roots; (a) Complex cepstrum ˆx[n], (b) Cepstrum c[n]. and negative quefrencies) depend on the window shape and its positioning with respect to the speech waveform. 8.5.3 Voiced Speech Analysis using the DFT The z-transform method of computing the short-time complex cepstrum yields the exact values of ˆx[n] (within computational error). This requires rooting of high-degree polynomials and evaluation of Eq. (8.67) for each n. Although this can be computationally demanding for large polynomials, it is made more feasible with root finders based on fast Fourier transform evaluations of the polynomial [21]. However, it is generally more efficient to use the DFT implementation discussed in Section 8.4.1. An example of the use of the DFT(FFT) in computation of the short-time complex cepstrum is shown in Figures 8.29 – 8.34 for the voiced segment of Figure 8.26. Figure 8.29 shows the DFT of the windowed speech segment, i.e., one frame of the short-time Fourier transform. 16 The thin line in Figure 8.29a shows the log magnitude of the DFT. The frequency-periodic component in this function is, of course, due to the time-periodic nature of the input, with the ripples being spaced approximately at multiples of the fundamental frequency. Figure 8.29c shows the discontinuous nature of the principal value of the phase, while the thin line in Figure 8.29b shows the unwrapped phase curve with discontinuities removed by addition of appropriate integer multiples of 2π at each 16 For the examples in this section, the DFT length was N = 4096. With this value, time aliasing is not a problem in the complex cepstrum, and plots of the DFT are a good approximation to a plot of the DTFT. Thus, for the most part it will not be necessary to distinguish between the “true” complex cepstrum ˆx[n] that would be obtained with the DTFT and ˜ ˆx[n] computed with the DFT.
DRAFT: L. R. Rabiner and R. W. Schafer, June 3, 2009 8.5. HOMOMORPHIC FILTERING OF NATURAL SPEECH 469 log magnitude Phase (Radians) Phase (Radians) 2 0 −2 (a) Log Magnitude −4 4096−point DFT of Windowed Signal −6 Estimate of Vocal Tract Spectrum 0 500 1000 1500 2000 2500 3000 3500 4000 5 0 −5 −10 (b) Unwrapped Phase 4096−point DFT of Windowed Signal Estimate of Vocal Tract Spectrum −15 0 500 1000 1500 2000 2500 3000 3500 4000 2 0 −2 (c) Principal Value Phase 0 500 1000 1500 2000 2500 3000 3500 4000 Frequency (Hz) 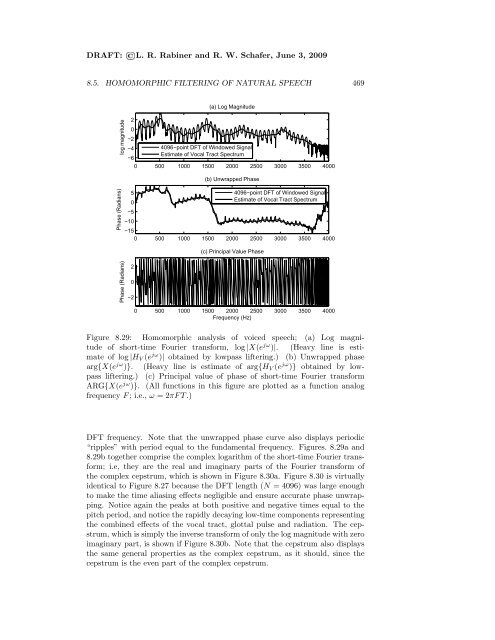Figure 8.29: Homomorphic analysis of voiced speech; (a) Log magnitude of short-time Fourier transform, log |X(e jω )|. (Heavy line is estimate of log |HV (e jω )| obtained by lowpass liftering.) (b) Unwrapped phase arg{X(e jω )}. (Heavy line is estimate of arg{HV (e jω )} obtained by lowpass liftering.) (c) Principal value of phase of short-time Fourier transform ARG{X(e jω )}. (All functions in this figure are plotted as a function analog frequency F ; i.e., ω = 2πF T .) DFT frequency. Note that the unwrapped phase curve also displays periodic “ripples” with period equal to the fundamental frequency. Figures. 8.29a and 8.29b together comprise the complex logarithm of the short-time Fourier transform; i.e, they are the real and imaginary parts of the Fourier transform of the complex cepstrum, which is shown in Figure 8.30a. Figure 8.30 is virtually identical to Figure 8.27 because the DFT length (N = 4096) was large enough to make the time aliasing effects negligible and ensure accurate phase unwrapping. Notice again the peaks at both positive and negative times equal to the pitch period, and notice the rapidly decaying low-time components representing the combined effects of the vocal tract, glottal pulse and radiation. The cepstrum, which is simply the inverse transform of only the log magnitude with zero imaginary part, is shown if Figure 8.30b. Note that the cepstrum also displays the same general properties as the complex cepstrum, as it should, since the cepstrum is the even part of the complex cepstrum.
Page 1 and 2: DRAFT: L. R. Rabiner and R. W. Scha
Page 45: DRAFT: L. R. Rabiner and R. W. Scha
Page 77: DRAFT: L. R. Rabiner and R. W. Scha

LR Rabiner and RW Schafer, June 3

Create successful ePaper yourself

Delete template?

Save as template?