Chapter 14 - Bootstrap Methods and Permutation Tests - WH Freeman

14-22 CHAPTER 14 Bootstrap Methods and Permutation Tests
800
Smooth
Regression line
600
Payoff
400
200
0 200 400 600 800 1000
Number
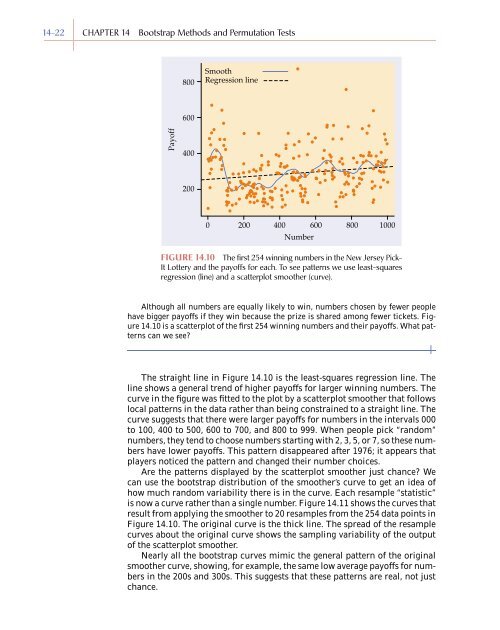
FIGURE 14.10 The first 254 winning numbers in the New Jersey Pick-
It Lottery and the payoffs for each. To see patterns we use least-squares
regression (line) and a scatterplot smoother (curve).
Although all numbers are equally likely to win, numbers chosen by fewer people
have bigger payoffs if they win because the prize is shared among fewer tickets. Figure
14.10 is a scatterplot of the first 254 winning numbers and their payoffs. What patterns
can we see?
The straight line in Figure 14.10 is the least-squares regression line. The
line shows a general trend of higher payoffs for larger winning numbers. The
curve in the figure was fitted to the plot by a scatterplot smoother that follows
local patterns in the data rather than being constrained to a straight line. The
curve suggests that there were larger payoffs for numbers in the intervals 000
to 100, 400 to 500, 600 to 700, and 800 to 999. When people pick “random”
numbers, they tend to choose numbers starting with 2, 3, 5, or 7, so these numbers
have lower payoffs. This pattern disappeared after 1976; it appears that
players noticed the pattern and changed their number choices.
Are the patterns displayed by the scatterplot smoother just chance? We
can use the bootstrap distribution of the smoother’s curve to get an idea of
how much random variability there is in the curve. Each resample “statistic”
is now a curve rather than a single number. Figure 14.11 shows the curves that
result from applying the smoother to 20 resamples from the 254 data points in
Figure 14.10. The original curve is the thick line. The spread of the resample
curves about the original curve shows the sampling variability of the output
of the scatterplot smoother.
Nearly all the bootstrap curves mimic the general pattern of the original
smoother curve, showing, for example, the same low average payoffs for numbers
in the 200s and 300s. This suggests that these patterns are real, not just
chance.