Self-Consistent Field Theory and Its Applications by M. W. Matsen
Self-Consistent Field Theory and Its Applications by M. W. Matsen
Self-Consistent Field Theory and Its Applications by M. W. Matsen
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
10 1 <strong>Self</strong>-consistent field theory <strong>and</strong> its applications<br />
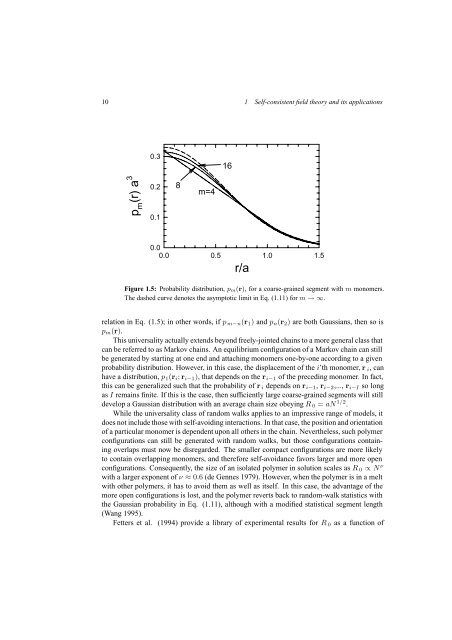
0.3<br />
16<br />
p m<br />
(r) a 3<br />
0.2<br />
0.1<br />
8<br />
m=4<br />
0.0<br />
0.0 0.5 1.0 1.5<br />
r/a<br />
Figure 1.5: Probability distribution, p m(r), for a coarse-grained segment with m monomers.<br />
The dashed curve denotes the asymptotic limit in Eq. (1.11) for m →∞.<br />
relation in Eq. (1.5); in other words, if p m−n (r 1 ) <strong>and</strong> p n (r 2 ) are both Gaussians, then so is<br />
p m (r).<br />
This universality actually extends beyond freely-jointed chains to a more general class that<br />
can be referred to as Markov chains. An equilibrium configuration of a Markov chain can still<br />
be generated <strong>by</strong> starting at one end <strong>and</strong> attaching monomers one-<strong>by</strong>-one according to a given<br />
probability distribution. However, in this case, the displacement of the i’th monomer, r i , can<br />
have a distribution, p 1 (r i ; r i−1 ), that depends on the r i−1 of the preceding monomer. In fact,<br />
this can be generalized such that the probability of r i depends on r i−1 , r i−2 ,..., r i−I so long<br />
as I remains finite. If this is the case, then sufficiently large coarse-grained segments will still<br />
develop a Gaussian distribution with an average chain size obeying R 0 = aN 1/2 .<br />
While the universality class of r<strong>and</strong>om walks applies to an impressive range of models, it<br />
does not include those with self-avoiding interactions. In that case, the position <strong>and</strong> orientation<br />
of a particular monomer is dependent upon all others in the chain. Nevertheless, such polymer<br />
configurations can still be generated with r<strong>and</strong>om walks, but those configurations containing<br />
overlaps must now be disregarded. The smaller compact configurations are more likely<br />
to contain overlapping monomers, <strong>and</strong> therefore self-avoidance favors larger <strong>and</strong> more open<br />
configurations. Consequently, the size of an isolated polymer in solution scales as R 0 ∝ N ν<br />
with a larger exponent of ν ≈ 0.6 (de Gennes 1979). However, when the polymer is in a melt<br />
with other polymers, it has to avoid them as well as itself. In this case, the advantage of the<br />
more open configurations is lost, <strong>and</strong> the polymer reverts back to r<strong>and</strong>om-walk statistics with<br />
the Gaussian probability in Eq. (1.11), although with a modified statistical segment length<br />
(Wang 1995).<br />
Fetters et al. (1994) provide a library of experimental results for R 0 as a function of