Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
86 Touching simplices<br />
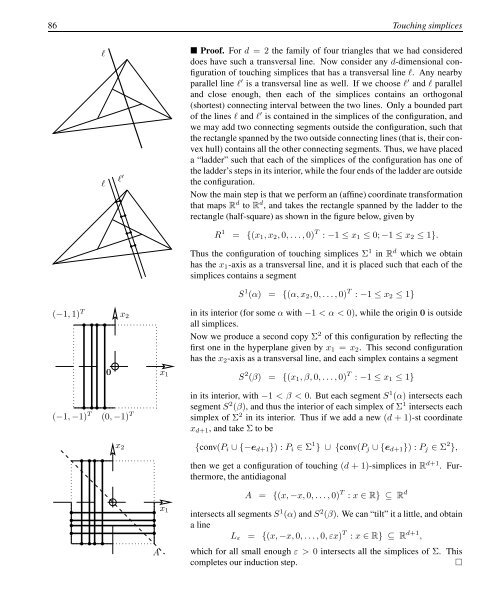
l<br />
l<br />
l ′<br />
Proof. For d = 2 the family of four triangles that we had considered<br />
does have such a transversal line. Now consider any d-dimensional configuration<br />
of touching simplices that has a transversal line l. Any nearby<br />
parallel line l ′ is a transversal line as well. If we choose l ′ and l parallel<br />
and close enough, then each of the simplices contains an orthogonal<br />
(shortest) connecting interval between the two lines. Only a bounded part<br />
of the lines l and l ′ is contained in the simplices of the configuration, and<br />
we may add two connecting segments outside the configuration, such that<br />
the rectangle spanned by the two outside connecting lines (that is, their convex<br />
hull) contains all the other connecting segments. Thus, we have placed<br />
a “ladder” such that each of the simplices of the configuration has one of<br />
the ladder’s steps in its interior, while the four ends of the ladder are outside<br />
the configuration.<br />
Now the main step is that we perform an (affine) coordinate transformation<br />
that maps R d to R d , and takes the rectangle spanned by the ladder to the<br />
rectangle (half-square) as shown in the figure below, given by<br />
(−1, 1) T x 2 in its interior (for some α with −1 < α < 0), while the origin 0 is outside<br />
R 1 = {(x 1 , x 2 , 0, . . .,0) T : −1 ≤ x 1 ≤ 0; −1 ≤ x 2 ≤ 1}.<br />
Thus the configuration of touching simplices Σ 1 in R d which we obtain<br />
has the x 1 -axis as a transversal line, and it is placed such that each of the<br />
simplices contains a segment<br />
S 1 (α) = {(α, x 2 , 0, . . .,0) T : −1 ≤ x 2 ≤ 1}<br />
all simplices.<br />
Now we produce a second copy Σ 2 of this configuration by reflecting the<br />
first one in the hyperplane given by x 1 = x 2 . This second configuration<br />
has the x 2 -axis as a transversal line, and each simplex contains a segment<br />
0 x 1<br />
S 2 (β) = {(x 1 , β, 0, . . .,0) T : −1 ≤ x 1 ≤ 1}<br />
(−1, −1) T<br />
(0, −1) T<br />
x 2<br />
in its interior, with −1 < β < 0. But each segment S 1 (α) intersects each<br />
segment S 2 (β), and thus the interior of each simplex of Σ 1 intersects each<br />
simplex of Σ 2 in its interior. Thus if we add a new (d + 1)-st coordinate<br />
x d+1 , and take Σ to be<br />
{conv(P i ∪ {−e d+1 }) : P i ∈ Σ 1 } ∪ {conv(P j ∪ {e d+1 }) : P j ∈ Σ 2 },<br />
A = {(x, −x, 0, . . . ,0) T : x ∈ R} ⊆ R d<br />
A<br />
then we get a configuration of touching (d + 1)-simplices in R d+1 . Fur-<br />
thermore, the antidiagonal<br />
x 1<br />
intersects all segments S 1 (α) and S 2 (β). We can “tilt” it a little, and obtain<br />
a line<br />
L ε = {(x, −x, 0, . . .,0, εx) T : x ∈ R} ⊆ R d+1 ,<br />
which for all small enough ε > 0 intersects all the simplices of Σ. This<br />
completes our induction step.<br />
□