Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
88 Touching simplices<br />
For our example, this matrix C is a (32 × 6)-matrix that starts<br />
⎛<br />
⎞<br />
1 1 1 1 1 1<br />
1 1 1 1 1 −1<br />
1 1 1 −1 1 1<br />
1 1 1 −1 1 −1<br />
1 −1 1 1 1 1<br />
C =<br />
1 −1 1 1 1 −1<br />
1 −1 1 −1 1 1<br />
,<br />
1 −1 1 −1 1 −1<br />
−1 −1 1 1 1 1<br />
⎜ −1 −1 1 1 1 −1<br />
⎟<br />
⎝<br />
. . . . . .<br />
⎠<br />
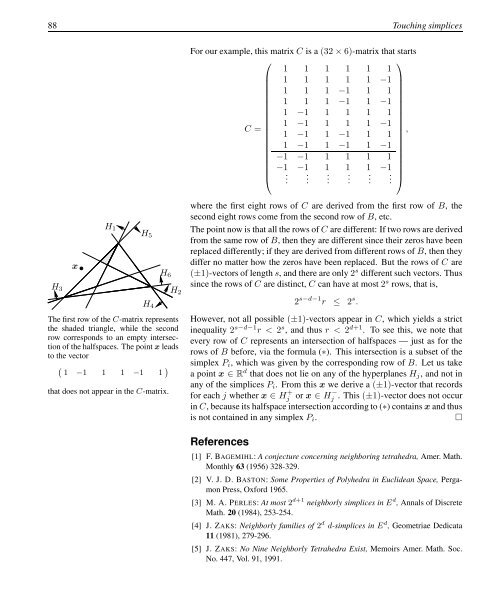
x<br />
H 1<br />
H 5<br />
H 6<br />
H 2<br />
where the first eight rows of C are derived from the first row of B, the<br />
second eight rows come from the second row of B, etc.<br />
The point now is that all the rows of C are different: If two rows are derived<br />
from the same row of B, then they are different since their zeros have been<br />
replaced differently; if they are derived from different rows of B, then they<br />
differ no matter how the zeros have been replaced. But the rows of C are<br />
(±1)-vectors of length s, and there are only 2 s different such vectors. Thus<br />
since the rows of C are distinct, C can have at most 2 s rows, that is,<br />
H 3<br />
H 4<br />
The first row of the C-matrix represents<br />
the shaded triangle, while the second<br />
row corresponds to an empty intersection<br />
of the halfspaces. The point x leads<br />
to the vector<br />
`<br />
1 −1 1 1 −1 1<br />
´<br />
that does not appear in the C-matrix.<br />
2 s−d−1 r ≤ 2 s .<br />
However, not all possible (±1)-vectors appear in C, which yields a strict<br />
inequality 2 s−d−1 r < 2 s , and thus r < 2 d+1 . To see this, we note that<br />
every row of C represents an intersection of halfspaces — just as for the<br />
rows of B before, via the formula (∗). This intersection is a subset of the<br />
simplex P i , which was given by the corresponding row of B. Let us take<br />
a point x ∈ R d that does not lie on any of the hyperplanes H j , and not in<br />
any of the simplices P i . From this x we derive a (±1)-vector that records<br />
for each j whether x ∈ H + j or x ∈ H − j . This (±1)-vector does not occur<br />
in C, because its halfspace intersection according to (∗) contains x and thus<br />
is not contained in any simplex P i .<br />
□<br />
References<br />
[1] F. BAGEMIHL: A conjecture concerning neighboring tetrahedra, Amer. Math.<br />
Monthly 63 (1956) 328-329.<br />
[2] V. J. D. BASTON: Some Properties of Polyhedra in Euclidean Space, Pergamon<br />
Press, Oxford 1965.<br />
[3] M. A. PERLES: At most 2 d+1 neighborly simplices in E d , Annals of Discrete<br />
Math. 20 (1984), 253-254.<br />
[4] J. ZAKS: Neighborly families of 2 d d-simplices in E d , Geometriae Dedicata<br />
11 (1981), 279-296.<br />
[5] J. ZAKS: No Nine Neighborly Tetrahedra Exist, Memoirs Amer. Math. Soc.<br />
No. 447, Vol. 91, 1991.