"Frontmatter". In: Analysis of Financial Time Series

More documents

Recommendations

Info

12 FINANCIAL TIME SERIES AND THEIR CHARACTERISTICSthere is no lower bound for r t , and the lower bound for R t is satisfied using 1 + R t =exp(r t ). However, the lognormal assumption is not consistent with all the propertiesof historical stock returns. In particular, many stock returns exhibit a positive excesskurtosis.Stable DistributionThe stable distributions are a natural generalization of normal in that they are stableunder addition, which meets the need of continuously compounded returns r t .Furthermore, stable distributions are capable of capturing excess kurtosis shown byhistorical stock returns. However, non-normal stable distributions do not have a finitevariance, which is in conflict with most finance theories. In addition, statistical modelingusing non-normal stable distributions is difficult. An example of non-normalstable distributions is the Cauchy distribution, which is symmetric with respect to itsmedian, but has infinite variance.Scale Mixture of Normal DistributionsRecent studies of stock returns tend to use scale mixture or finite mixture of normaldistributions. Under the assumption of scale mixture of normal distributions, the logreturn r t is normally distributed with mean µ and variance σ 2 [i.e., r t ∼ N(µ, σ 2 )].However, σ 2 is a random variable that follows a positive distribution (e.g., σ −2 followsa Gamma distribution). An example of finite mixture of normal distributionsisr t ∼ (1 − X)N(µ, σ 2 1 ) + XN(µ, σ 2 2 ),where 0 ≤ α ≤ 1, σ1 2 is small and σ 2 2 is relatively large. For instance, with α =0.05, the finite mixture says that 95% of the returns follow N(µ, σ1 2 ) and 5% followN(µ, σ2 2). The large value of σ 2 2 enables the mixture to put more mass at the tails ofits distribution. The low percentage of returns that are from N(µ, σ2 2 ) says that themajority of the returns follow a simple normal distribution. Advantages of mixturesof normal include that they maintain the tractability of normal, have finite higherorder moments, and can capture the excess kurtosis. Yet it is hard to estimate themixture parameters (e.g., the α in the finite-mixture case).Figure 1.1 shows the probability density functions of a finite mixture of normal,Cauchy, and standard normal random variable. The finite mixture of normalis 0.95N(0, 1) + 0.05N(0, 16) and the density function of Cauchy isf (x) =1π(1 + x 2 , −∞ < x < ∞.)It is seen that Cauchy distribution has fatter tails than the finite mixture of normal,which in turn has fatter tails than the standard normal.
DISTRIBUTIONAL PROPERTIES OF RETURNS 13f(x)0.0 0.1 0.2 0.3 0.4MixtureCauchyNormal-4 -2 0 2 4xFigure 1.1. Comparison of finite-mixture, stable, and standard normal density functions.1.2.3 Multivariate ReturnsLet r t = (r 1t ,...,r Nt ) ′ be the log returns of N assets at time t. The multivariateanalyses of Chapters 8 and 9 are concerned with the joint distribution of {r t }t=1 T .This joint distribution can be partitioned in the same way as that of Eq. (1.15). Theanalysis is then focused on the specification of the conditional distribution functionF(r t | r t−1 ,...,r 1 , θ). In particular, how the conditional expectation and conditionalcovariance matrix of r t evolve over time constitute the main subjects of Chapters 8and 9.The mean vector and covariance matrix of a random vector X = (X 1 ,...,X p ) aredefined asE(X) = µ x =[E(X 1 ),...,E(X p )] ′ ,Cov(X) = Σ x = E[(X − µ x )(X − µ x ) ′ ]provided that the expectations involved exist. When the data {x 1 ,...,x T } of X areavailable, the sample mean and covariance matrix are defined aŝµ x = 1 TT∑x t ,t=1̂Σ x = 1 TT∑(x t − ̂µ x )(x t − ̂µ x ) ′ .t=1
Page 1 and 2: Analysis of FinancialTime SeriesFin
Page 3 and 4: ContentsPrefacexi1. Financial Time
Page 5 and 6: CONTENTSix6.6 Black-Scholes Pricing
Page 7 and 8: PrefaceThis book grew out of an MBA
Page 9 and 10: Analysis of Financial Time Series.
Page 11 and 12: ASSET RETURNS 3Multiperiod Simple R
Page 13 and 14: ASSET RETURNS 5r t [k] =ln(1 + R t
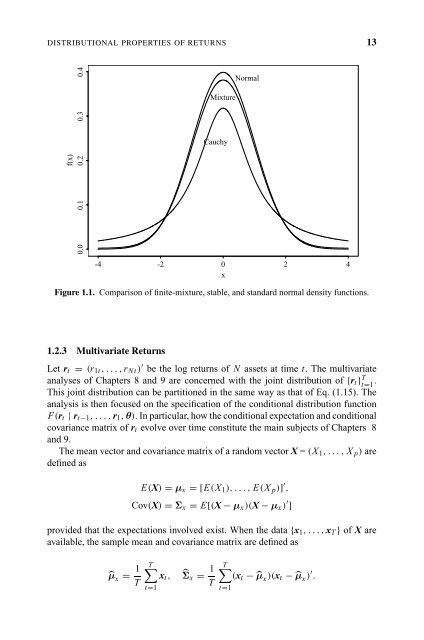
Page 15 and 16: DISTRIBUTIONAL PROPERTIES OF RETURN
Page 18 and 19: 10 FINANCIAL TIME SERIES AND THEIR
Page 26: 18 FINANCIAL TIME SERIES AND THEIR
Page 29 and 30: REFERENCES 21Federal Reserve Bank o
Page 31 and 32: CORRELATION AND AUTOCORRELATION FUN
Page 33 and 34: CORRELATION AND AUTOCORRELATION FUN
Page 35 and 36: WHITE NOISE AND LINEAR TIME SERIES
Page 37 and 38: SIMPLE AUTOREGRESSIVE MODELS 29whic
Page 39 and 40: SIMPLE AUTOREGRESSIVE MODELS 31wher
Page 41 and 42: SIMPLE AUTOREGRESSIVE MODELS 33wher
Page 43 and 44: SIMPLE AUTOREGRESSIVE MODELS 35expa
Page 45 and 46: SIMPLE AUTOREGRESSIVE MODELS 37Tabl
Page 47 and 48: SIMPLE AUTOREGRESSIVE MODELS 39Mode
Page 49 and 50: SIMPLE AUTOREGRESSIVE MODELS 41The
Page 51 and 52: SIMPLE MOVING-AVERAGE MODELS 43wher
Page 53 and 54: SIMPLE MOVING-AVERAGE MODELS 45s-rt
Page 55 and 56: SIMPLE MOVING-AVERAGE MODELS 47The
Page 57 and 58: SIMPLE ARMA MODELS 49A time series
Page 59 and 60: SIMPLE ARMA MODELS 51operator, the
Page 61 and 62: SIMPLE ARMA MODELS 53Table 2.5. Sam
Page 63 and 64: SIMPLE ARMA MODELS 55This represent
Page 65 and 66: UNIT-ROOT NONSTATIONARITY 57ˆp h (
Page 67 and 68: UNIT-ROOT NONSTATIONARITY 59log-pri
Page 69 and 70: SEASONAL MODELS 61which is commonly
Page 71 and 72:
SEASONAL MODELS 63Series : xSeries
Page 73 and 74:
SEASONAL MODELS 65models use the sa
Page 75 and 76:
• ••• •••••••
Page 77 and 78:
REGRESSION MODELS WITH TIME SERIES
Page 79 and 80:
REGRESSION MODELS WITH TIME SERIES
Page 81 and 82:
LONG-MEMORY MODELS 73=(k − d −
Page 83 and 84:
APPENDIX A: SOME SCA COMMANDS 75est
Page 85 and 86:
EXERCISES 77relation. Draw your con
Page 87 and 88:
Analysis of Financial Time Series.
Page 89 and 90:
STRUCTURE OF A MODEL 813.2 STRUCTUR
Page 91 and 92:
THE ARCH MODEL 83corrected asset re
Page 93 and 94:
THE ARCH MODEL 85Series : xACF0.0 0
Page 95 and 96:
THE ARCH MODEL 87sample mean from t
Page 97 and 98:
THE ARCH MODEL 89where Ɣ(x) is the
Page 99 and 100:
THE ARCH MODEL 91Series : resiSerie
Page 101 and 102:
THE GARCH MODEL 93other softwares a
Page 103 and 104:
THE GARCH MODEL 95ahead forecast ca
Page 105 and 106:
THE GARCH MODEL 97The fitted AR(3)
Page 107 and 108:
THE GARCH MODEL 99Series : stdatACF
Page 109 and 110:
THE GARCH-M MODEL 101two models. Th
Page 111 and 112:
THE EXPONENTIAL GARCH MODEL 103To b
Page 113 and 114:
THE EXPONENTIAL GARCH MODEL 105eros
Page 115 and 116:
THE CHARMA MODEL 107ˆσ 2 864 (3)
Page 117 and 118:
RANDOM COEFFICIENT AUTOREGRESSIVE M
Page 119 and 120:
THE LONG-MEMORY STOCHASTIC VOLATILI
Page 121 and 122:
AN ALTERNATIVE APPROACH 113where Va
Page 123 and 124:
APPLICATION 115(a) IBMlog-rtn-30 -1
Page 125 and 126:
APPLICATION 117equationThe fitted m
Page 127 and 128:
KURTOSIS OF GARCH MODELS 119where K
Page 129 and 130:
SOME RATS PROGRAMS FOR ESTIMATING V
Page 131 and 132:
EXERCISES 123• Is there evidence
Page 133 and 134:
REFERENCES 125Melino, A., and Turnb
Page 135 and 136:
NONLINEAR TIME SERIES 127To put non
Page 137 and 138:
NONLINEAR MODELS 129Example 4.1. Co
Page 139 and 140:
NONLINEAR MODELS 131jumps when it b
Page 141 and 142:
NONLINEAR MODELS 133the series and
Page 143 and 144:
NONLINEAR MODELS 135els to the mont
Page 145 and 146:
NONLINEAR MODELS 137growth-2 -1 0 1
Page 147 and 148:
NONLINEAR MODELS 139average of y t
Page 149 and 150:
NONLINEAR MODELS 141indicating that
Page 151 and 152:
NONLINEAR MODELS 143s T,2t=1T∑K h
Page 153 and 154:
NONLINEAR MODELS 145f i (.) of Eq.
Page 155 and 156:
NONLINEAR MODELS 1474.1.9.1 Feed-Fo
Page 157 and 158:
NONLINEAR MODELS 1494.1.9.2 Trainin
Page 159 and 160:
NONLINEAR MODELS 151prob0.0 0.2 0.4
Page 161 and 162:
NONLINEARITY TESTS 153idea behind v
Page 163 and 164:
NONLINEARITY TESTS 155C l (δ, T )
Page 165 and 166:
NONLINEARITY TESTS 157and obtain th
Page 167 and 168:
NONLINEARITY TESTS 159• Step 2: C
Page 169 and 170:
FORECASTING 161returns. In summary,
Page 171 and 172:
FORECASTING 163in m 11 and m 22 ind
Page 173 and 174:
APPLICATION 165unem. rate4 6 8 10
Page 175 and 176:
APPLICATION 167Table 4.4. Out-of-Sa
Page 177 and 178:
APPENDIX A 169compute a0 = 0.1, a1
Page 179 and 180:
REFERENCES 171P(s t = 2 | s t−1 =
Page 181 and 182:
REFERENCES 173Fan, J. (1993), “Lo
Page 183 and 184:
Page 185 and 186:
NONSYNCHRONOUS TRADING 177t − k t
Page 187 and 188:
BID-ASK SPREAD 179The lag-1 autocov
Page 189 and 190:
EMPIRICAL CHARACTERISTICS 181The ma
Page 191 and 192:
n(trades)0 20406080 1200 1000 2000
Page 193 and 194:
EMPIRICAL CHARACTERISTICS 185after-
Page 195 and 196:
MODELS FOR PRICE CHANGES 187deep un
Page 197 and 198:
MODELS FOR PRICE CHANGES 189σ 2i (
Page 199 and 200:
MODELS FOR PRICE CHANGES 191A i = 1
Page 201 and 202:
MODELS FOR PRICE CHANGES 193( )piln
Page 203 and 204:
DURATION MODELS 195For the IBM data
Page 205 and 206:
DURATION MODELS 197(a) is the avera
Page 207 and 208:
DURATION MODELS 199actions might no
Page 209 and 210:
DURATION MODELS 201Series : xACF0.0
Page 211 and 212:
DURATION MODELS 203reduces to that
Page 213 and 214:
DURATION MODELS 205Series : xACF0.0
Page 215 and 216:
THE PCD MODEL 207where w(α) denote
Page 217 and 218:
THE PCD MODEL 209(a) All transactio
Page 219 and 220:
THE PCD MODEL 2110 10 20 30 40 500
Page 221 and 222:
THE PCD MODEL 213⎧⎪⎨1f (x |
Page 223 and 224:
THE PCD MODEL 215Generalized Gamma
Page 225 and 226:
THE PCD MODEL 217smpl 2 3534compute
Page 227 and 228:
REFERENCES 219(a) Use the data to c
Page 229 and 230:
Page 231 and 232:
STOCHASTIC PROCESSES 223write a con
Page 233 and 234:
STOCHASTIC PROCESSES 2253. stationa
Page 235 and 236:
ITO’S LEMMA 2276.3.2 Stochastic D
Page 237 and 238:
ITO’S LEMMA 229This result shows
Page 239 and 240:
DISTRIBUTIONS OF PRICE AND RETURN 2
Page 241 and 242:
BLACK-SCHOLES EQUATION 233and G t =
Page 243 and 244:
BLACK-SCHOLES FORMULA 235risk prefe
Page 245 and 246:
BLACK-SCHOLES FORMULA 237The stock
Page 247 and 248:
BLACK-SCHOLES FORMULA 239(a) Call o
Page 249 and 250:
AN EXTENSION OF ITO’S LEMMA 2410
Page 251 and 252:
STOCHASTIC INTEGRAL 243using the It
Page 253 and 254:
JUMP DIFFUSION MODELS 245where w t
Page 255 and 256:
JUMP DIFFUSION MODELS 247where it i
Page 257 and 258:
JUMP DIFFUSION MODELS 249sudden jum
Page 259 and 260:
APPENDIX A 251Pricing formulas for
Page 261 and 262:
EXERCISES 253which involves the CDF
Page 263 and 264:
REFERENCES 255Bakshi, G., Cao, C.,
Page 265 and 266:
VALUEATRISK 257log return-0.2 -0.1
Page 267 and 268:
RISKMETRICS 259we use log returns r
Page 269 and 270:
RISKMETRICS 261investor is$10,000,0
Page 271 and 272:
ECONOMETRIC APPROACH TO VAR 263Cons
Page 273 and 274:
ECONOMETRIC APPROACH TO VAR 265The
Page 275 and 276:
QUANTILE ESTIMATION 267Using the fo
Page 277 and 278:
QUANTILE ESTIMATION 269ˆx 0.01 = p
Page 279 and 280:
EXTREME VALUE THEORY 271= 1 −= 1
Page 281 and 282:
EXTREME VALUE THEORY 273shows that
Page 283 and 284:
EXTREME VALUE THEORY 275{ [] }r n(i
Page 285 and 286:
EXTREME VALUE THEORY 2777.5.3 Appli
Page 287 and 288:
EXTREME VALUE TO VAR 2797.6 AN EXTR
Page 289 and 290:
EXTREME VALUE TO VAR 281VaR =−2.5
Page 291 and 292:
EXTREME VALUE TO VAR 283stock. The
Page 293 and 294:
A NEW APPROACH TO VAR 285series (e.
Page 295 and 296:
A NEW APPROACH TO VAR 287In Eq. (7.
Page 297 and 298:
A NEW APPROACH TO VAR 289Example 7.
Page 299 and 300:
A NEW APPROACH TO VAR 291feature is
Page 301 and 302:
A NEW APPROACH TO VAR 293(a) Homoge
Page 303 and 304:
A NEW APPROACH TO VAR 295Table 7.4.
Page 305 and 306:
REFERENCES 297a Gaussian GARCH(1, 1
Page 307 and 308:
Page 309 and 310:
CROSS-CORRELATION 301correlation co
Page 311 and 312:
CROSS-CORRELATION 303where ̂D is t
Page 313 and 314:
CROSS-CORRELATION 305Table 8.1. Sum
Page 315 and 316:
30yr20yr10yr5yr1yr-10 0 510-10 0 51
Page 317 and 318:
VAR MODELS 3098.2 VECTOR AUTOREGRES
Page 319 and 320:
VAR MODELS 311where G = Cov(b t ).
Page 321 and 322:
VAR MODELS 313where φ 0 and a t ar
Page 323 and 324:
VAR MODELS 315To specify the order
Page 325 and 326:
VAR MODELS 317the S&P 500 index. Th
Page 327 and 328:
VECTOR MA MODELS 319[ ] [ ] [ ] [r1
Page 329 and 330:
VECTOR MA MODELS 321turn used to co
Page 331 and 332:
VECTOR ARMA MODELS 323For the VAR(1
Page 333 and 334:
VECTOR ARMA MODELS 325log-rate0.0 0
Page 335 and 336:
VECTOR ARMA MODELS 327interest-rate
Page 337 and 338:
CO-INTEGRATION 329Series : x1ACF0.0
Page 339 and 340:
CO-INTEGRATION 331Stock Exchange; o
Page 341 and 342:
THRESHOLD CO-INTEGRATION 333ously b
Page 343 and 344:
PRINCIPAL COMPONENT ANALYSIS 3358.6
Page 345 and 346:
PRINCIPAL COMPONENT ANALYSIS 337(c
Page 347 and 348:
PRINCIPAL COMPONENT ANALYSIS 339(a)
Page 349 and 350:
FACTOR ANALYSIS 341(a) 5 stock retu
Page 351 and 352:
FACTOR ANALYSIS 343andCov(r, F) = E
Page 353 and 354:
FACTOR ANALYSIS 345matrix P to tran
Page 355 and 356:
FACTOR ANALYSIS 347Example 8.9. In
Page 357 and 358:
APPENDIX A. REVIEW OF VECTORS AND M
Page 359 and 360:
APPENDIX A. REVIEW OF VECTORS AND M
Page 361 and 362:
APPENDIX B. MULTIVARIATE NORMAL DIS
Page 363 and 364:
REFERENCES 355(b) Build a bivariate
Page 365 and 366:
Page 367 and 368:
REPARAMETERIZATION 359To illustrate
Page 369 and 370:
REPARAMETERIZATION 361where ⊥ den
Page 371 and 372:
GARCH MODELS FOR BIVARIATE RETURNS
Page 373 and 374:
Page 375 and 376:
Page 377 and 378:
Page 379 and 380:
Page 381 and 382:
Page 383 and 384:
Page 385 and 386:
VECTOR VOLATILITY MODELS 377using t
Page 387 and 388:
VECTOR VOLATILITY MODELS 379large-c
Page 389 and 390:
VECTOR VOLATILITY MODELS 381(a) S&P
Page 391 and 392:
FACTOR-VOLATILITY MODELS 383conside
Page 393 and 394:
APPLICATION 385[ ]σ11,t=σ 22,t⎡
Page 395 and 396:
MULTIVARIATE t DISTRIBUTION 387σ 1
Page 397 and 398:
APPENDIX A. SOME REMARKS ON ESTIMAT
Page 399 and 400:
APPENDIX A. SOME REMARKS ON ESTIMAT
Page 401 and 402:
REFERENCES 393(a) Compute the sampl
Page 403 and 404:
Page 405 and 406:
GIBBS SAMPLING 397mean adding auxil
Page 407 and 408:
BAYESIAN INFERENCE 399distributions
Page 409 and 410:
BAYESIAN INFERENCE 401normal with m
Page 411 and 412:
ALTERNATIVE ALGORITHMS 403distribut
Page 413 and 414:
ALTERNATIVE ALGORITHMS 40510.4.2 Me
Page 415 and 416:
REGRESSION WITH SERIAL CORRELATIONS
Page 417 and 418:
REGRESSION WITH SERIAL CORRELATIONS
Page 419 and 420:
MISSING VALUES AND OUTLIERS 411y h
Page 421 and 422:
MISSING VALUES AND OUTLIERS 413Cons
Page 423 and 424:
MISSING VALUES AND OUTLIERS 415we h
Page 425 and 426:
MISSING VALUES AND OUTLIERS 417c3t-
Page 427 and 428:
STOCHASTIC VOLATILITY MODELS 419tha
Page 429 and 430:
STOCHASTIC VOLATILITY MODELS 421whe
Page 431 and 432:
STOCHASTIC VOLATILITY MODELS 423den
Page 433 and 434:
STOCHASTIC VOLATILITY MODELS 425The
Page 435 and 436:
STOCHASTIC VOLATILITY MODELS 427(a)
Page 437 and 438:
•••MARKOV SWITCHING MODELS 42
Page 439 and 440:
MARKOV SWITCHING MODELS 431(a) GARC
Page 441 and 442:
MARKOV SWITCHING MODELS 433β i ∼
Page 443 and 444:
MARKOV SWITCHING MODELS 435(a) mont
Page 445 and 446:
MARKOV SWITCHING MODELS 437α ij ar
Page 447 and 448:
FORECASTING 439garchrtn-sq0 200 400
Page 449 and 450:
EXERCISES 441eter uncertainty in pr
Page 451 and 452:
REFERENCES 443Justel, A., Peña, D.
Page 453 and 454:
446 INDEXData (cont.)equal-weighted
Page 455:
448 INDEXPoisson process, 244inhomo
show all

"Frontmatter". In: Analysis of Financial Time Series

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?