ch01-03 stress & strain & properties

01 Solutions 46060 5/6/10 2:43 PM Page 50
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently
exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
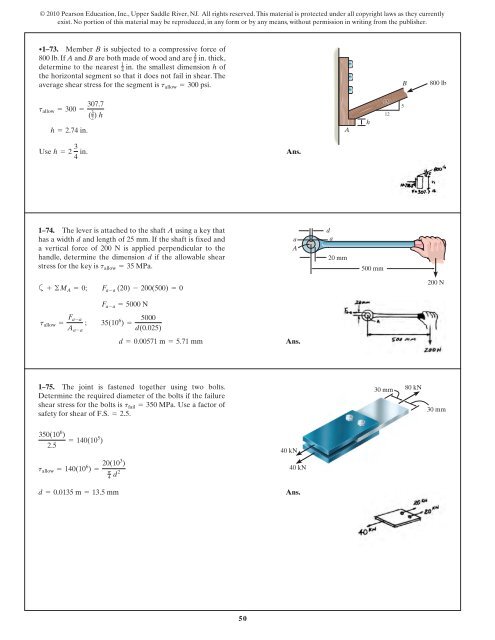
•1–73. Member B is subjected to a compressive force of
3
800 lb. If A and B are both made of wood and are thick,
1
determine to the nearest
4 in. 8 in.
the smallest dimension h of
the horizontal segment so that it does not fail in shear. The
average shear stress for the segment is t allow = 300 psi.
B 800 lb
t allow = 300 = 307.7
( 3 2 ) h
h = 2.74 in.
A
h
13
12
5
Use h = 2 3 4 in.
Ans.
1–74. The lever is attached to the shaft A using a key that
has a width d and length of 25 mm. If the shaft is fixed and
a vertical force of 200 N is applied perpendicular to the
handle, determine the dimension d if the allowable shear
stress for the key is t allow = 35 MPa.
a
A
d
a
20 mm
500 mm
a + ©M A = 0; F a - a (20) - 200(500) = 0
200 N
F a - a = 5000 N
t allow = F a - a
A a - a
; 35(10 6 ) =
5000
d(0.025)
d = 0.00571 m = 5.71 mm
Ans.
1–75. The joint is fastened together using two bolts.
Determine the required diameter of the bolts if the failure
shear stress for the bolts is t fail = 350 MPa. Use a factor of
safety for shear of F.S. = 2.5.
30 mm
80 kN
30 mm
350(10 6 )
2.5
= 140(10 5 )
t allow = 140(10 6 ) = 20(103 )
p
4 d2
d = 0.0135 m = 13.5 mm
40 kN
40 kN
Ans.
50