ch01-03 stress & strain & properties

02 Solutions 46060 5/6/10 1:45 PM Page 18
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently
exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
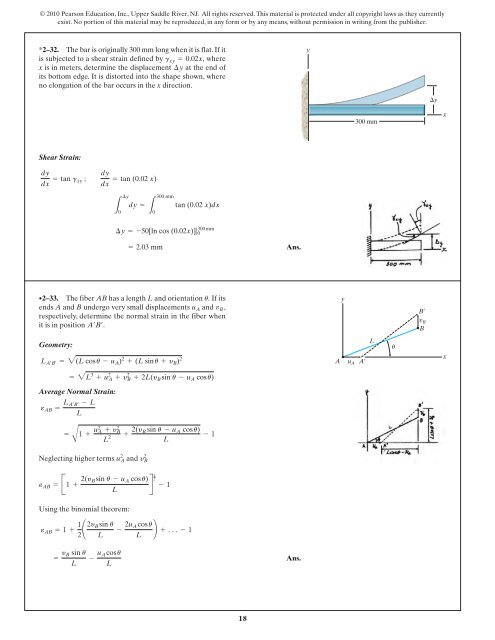
*2–32. The bar is originally 300 mm long when it is flat. If it
is subjected to a shear strain defined by g xy = 0.02x, where
x is in meters, determine the displacement ¢y at the end of
its bottom edge. It is distorted into the shape shown, where
no elongation of the bar occurs in the x direction.
y
y
300 mm
x
Shear Strain:
dy
dx = tan g xy ; dy
dx
= tan (0.02 x)
L0
¢y
300 mm
dy = tan (0.02 x)dx
L
0
300 mm
¢y = -50[ln cos (0.02x)]| 0
= 2.03 mm
Ans.
•2–33. The fiber AB has a length L and orientation u. If its
ends A and B undergo very small displacements u A and v B ,
respectively, determine the normal strain in the fiber when
it is in position A¿B¿.
y
B¿
v B
B
Geometry:
L A¿B¿ = 2(L cos u - u A ) 2 + (L sin u + y B ) 2
A
u A A¿
L
u
x
= 2L 3 + u A 2 + y B 2 + 2L(y B sin u - u A cos u)
Average Normal Strain:
e AB = L A¿B¿ - L
L
= 1 + u A 2 + y 2 B
A L 2 + 2(y B sin u - u A cos u)
- 1
L
Neglecting higher terms
u A
2
and
y 2 B
e AB = B1 + 2(y B sin u - u A cos u)
L
Using the binomial theorem:
1
2
R - 1
e AB = 1 + 1 2 ¢ 2y B sin u
L
- 2u A cos u ≤ + . . . - 1
L
= y B sin u
L
- u A cos u
L
Ans.
18