Doing the Math - JHU Mathematics - Johns Hopkins University

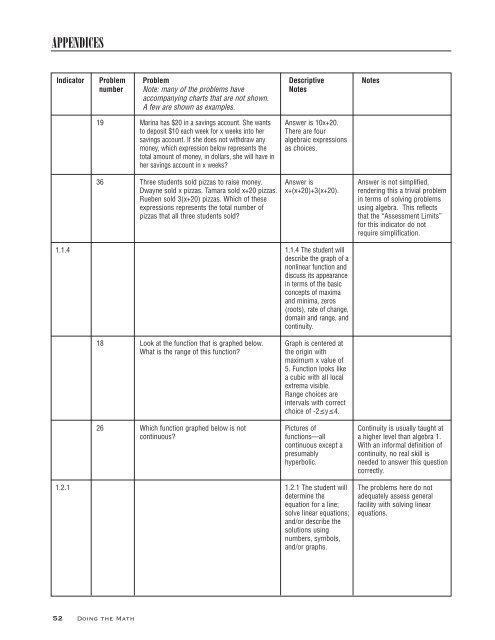
APPENDICES
Indicator Problem Problem Descriptive Notes
number Note: many of the problems have Notes
accompanying charts that are not shown.
A few are shown as examples.
1.1.4
1.2.1
19
36
18
26
52 Doing the Math
Marina has $20 in a savings account. She wants
to deposit $10 each week for x weeks into her
savings account. If she does not withdraw any
money, which expression below represents the
total amount of money, in dollars, she will have in
her savings account in x weeks?
Three students sold pizzas to raise money.
Dwayne sold x pizzas. Tamara sold x+20 pizzas.
Rueben sold 3(x+20) pizzas. Which of these
expressions represents the total number of
pizzas that all three students sold?
Look at the function that is graphed below.
What is the range of this function?
Which function graphed below is not
continuous?
Answer is 10x+20.
There are four
algebraic expressions
as choices.
Answer is
x+(x+20)+3(x+20).
1.1.4 The student will
describe the graph of a
nonlinear function and
discuss its appearance
in terms of the basic
concepts of maxima
and minima, zeros
(roots), rate of change,
domain and range, and
continuity.
Graph is centered at
the origin with
maximum x value of
5. Function looks like
a cubic with all local
extrema visible.
Range choices are
intervals with correct
choice of -2≤y≤4.
Pictures of
functions—all
continuous except a
presumably
hyperbolic.
1.2.1 The student will
determine the
equation for a line;
solve linear equations;
and/or describe the
solutions using
numbers, symbols,
and/or graphs.
Answer is not simplified,
rendering this a trivial problem
in terms of solving problems
using algebra. This reflects
that the “Assessment Limits”
for this indicator do not
require simplification.
Continuity is usually taught at
a higher level than algebra 1.
With an informal definition of
continuity, no real skill is
needed to answer this question
correctly.
The problems here do not
adequately assess general
facility with solving linear
equations.