2. hét: Az alakváltozás fogalma, kis és nagy alakváltozások ...

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
2. hét: Az alakváltozás fogalma, kis és nagy alakváltozások,
alakváltozás-tenzorok, főnyúlások
1. 1D alakváltozások vizsgálata
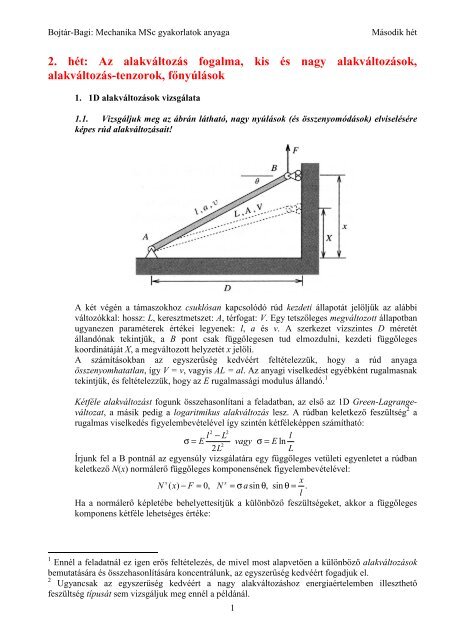
1.1. Vizsgáljuk meg az ábrán látható, nagy nyúlások (és összenyomódások) elviselésére
képes rúd alakváltozásait!
A két végén a támaszokhoz csuklósan kapcsolódó rúd kezdeti állapotát jelöljük az alábbi
változókkal: hossz: L, keresztmetszet: A, térfogat: V. Egy tetszőleges megváltozott állapotban
ugyanezen paraméterek értékei legyenek: l, a és v. A szerkezet vízszintes D méretét
állandónak tekintjük, a B pont csak függőlegesen tud elmozdulni, kezdeti függőleges
koordinátáját X, a megváltozott helyzetét x jelöli.
A számításokban az egyszerűség kedvéért feltételezzük, hogy a rúd anyaga
összenyomhatatlan, így V = v, vagyis AL = al. Az anyagi viselkedést egyébként rugalmasnak
tekintjük, és feltételezzük, hogy az E rugalmassági modulus állandó. 1
Kétféle alakváltozást fogunk összehasonlítani a feladatban, az első az 1D Green-Lagrangeváltozat,
a másik pedig a logaritmikus alakváltozás lesz. A rúdban keletkező feszültség 2 a
rugalmas viselkedés figyelembevételével így szintén kétféleképpen számítható:
2 2
l − L l
σ = E vagy σ = E ln
2
2L
L
Írjunk fel a B pontnál az egyensúly vizsgálatára egy függőleges vetületi egyenletet a rúdban
keletkező N(x) normálerő függőleges komponensének figyelembevételével:
N ( x) − F = 0, N = σ asin
θ, sin θ = .
l
Ha a normálerő képletébe behelyettesítjük a különböző feszültségeket, akkor a függőleges
komponens kétféle lehetséges értéke:
x x x
1 Ennél a feladatnál ez igen erős feltételezés, de mivel most alapvetően a különböző alakváltozások
bemutatására és összehasonlítására koncentrálunk, az egyszerűség kedvéért fogadjuk el.
2 Ugyancsak az egyszerűség kedvéért a nagy alakváltozáshoz energiaértelemben illeszthető
feszültség típusát sem vizsgáljuk meg ennél a példánál.
1

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
2 2
x Evx ⎛ l − L ⎞
x Evx l
N = vagy N ln
2 ⎜ 2 ⎟ = .
2
l ⎝ 2L
⎠
l L
2 2 2
Megjegyezzük, hogy mivel l = D + x , így a normálerő x nemlineáris függvénye lesz.
Ha az F külső erő egy megadott értékéhez akarjuk kiszámítani az egyensúlyi állapotnak
megfelelő x koordináta nagyságát, akkor a fenti nemlineáris egyenleteket kell megoldanunk.
Természetesen sokkal egyszerűbb a fordított feladat: adott x értékéhez kiszámítani a
szükséges F nagyságát, ezért a továbbiakban ezt a gondolatmenetet követjük.
45 fokos kezdeti állapot esetére megoldva ezt a feladatot egy ábrán feltüntettük a kétféle
alakváltozáshoz tartozó (EA-val illetve L-lel normált) F – x kapcsolatot:
A következő ábrán egy olyan rudat vizsgáltunk, amelynek kezdeti helyzete függőleges volt:
2
Logaritmikus
Logaritmikus

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
A példához tartozó utolsó ábra egy vízszintes kezdeti állapotú rúdelem állapotváltozását
mutatja:
Befejezésül még megjegyezzük, hogy a B csomópontnál végrehajtott egyensúlyi vizsgálatból
egyszerű és érdekes következtetés vonható le a szerkezet függőleges merevségének
vizsgálatára. Jelöljük például a vetületi egyenletben szereplő két tag különbségét az alábbi
módon R(x)-szel:
x
R( x) = N ( x) − F .
Ez a változó zérus értékű az egyensúly teljesülése esetén, változása pedig a rendszer
függőleges irányú ellenállását, merevségét jelzi. Ha F állandó, akkor:
x
dR dN d ⎛ σVx ⎞ ⎛ ax dσ 2σax
⎞ dl σa
K = = = ⎜ 2 ⎟ = ⎜ − 2 ⎟ + =
dx dx dx ⎝ l ⎠ ⎝ l dl l ⎠ dx l
2
⎛ dσ 2σ
⎞ x σa
a ⎜ ⎟ 2
dl l l l
=
⎝
−
⎠
+ .
A képlethez még szükséges dσ / dl deriváltat az egyes alakváltozások segítségével lehet
felírni. Jelen esetben:
2 vagy
⎛ dσ ⎞
⎜ ⎟
⎝ dl ⎠GL El
=
L
⎛ dσ ⎞
⎜ ⎟
⎝ dl ⎠Log
E
= ,
l
így a kétféle merevség:
2 2
A ⎛ L ⎞ x σa KGL = ⎜ E − 2σ 2 ⎟ + 2
L ⎝ l ⎠ l l
vagy
2
a x σa
K Log = ( E − 2σ
) + .
2
l l l
Sok hasonló elem fedezhető fel a képletekben, de (ahogy azt az előző ábrákon is láthattuk)
értékük a különböző alakváltozás-modellek miatt nem azonos, csupán a kezdeti X
konfigurációhoz nagyon közeli x esetén (ahol a ≈ A, l ≈ L ) mondhatjuk, hogy KGL ≈ KLog
.
1.2. Bizonyítsuk be, hogy 1D esetben a térfogatváltozásra jellemző J determináns
kifejezhető a λ nyúlási- és a ν Poisson-tényező segítségével!
A rúd keresztmetszete az egyszerűség kedvéért legyen kör. Egy tetszőleges pillanatnyi
állapot adatai:
2
sugár: r, hossz: l, keresztmetszet: a = r π, térfogat: v = al .
A változásokat növekményi szinten vizsgálva:
3
Logaritmikus

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
alakváltozás a hossztengely irányában:
térfogatváltozás: d v = a dl + l da .
dl
ε = , alakváltozás sugár irányban: r
l
4
dr dl
r l
ε = = −ν ,
Mivel a terület növekménye
dr dl
da = 2π r dr = 2a = −2aν , így a térfogatváltozás:
r l
d v = a dl − 2aν dl = 1− 2ν
a dl .
( )
d v dl
Innen: = ( 1− 2ν
) . Ha feltételezzük, hogy a Poisson-tényező konstans a deformáció
v l
során, akkor a kezdeti és a pillanatnyi állapot között integrálva:
v
l
d v dl v
l
∫ = (1− 2 ν) ln (1 2 )ln
v ∫ ⇒ = − ν .
l V L
Innen:
V L
(1−2 ν)
v ⎛ l ⎞
= J = ⎜ ⎟ = λ
V ⎝ L ⎠
(1−2 ν)
2. Többdimenziós alakváltozások vizsgálata
2.1. Egy kör alakra hajlított lemezcsíkon mutassuk be a Green-Lagrange- és az
Almansi-Hamel-féle alakváltozási tenzorok számításának lépéseit!
Ez a feladat átmenetet képez a korábban vizsgált 1D és az „igazi” többdimenziós
alakváltozás-állapotok között, hiszen a – sík alakváltozási állapotúnak feltételezett – lemez a
kétdimenziós térben végez elmozdulást, de – mint látni fogjuk – alakváltozásai a szerkezet
jellegéből adódóan egydimenziósak.
Megváltozott állapot
Az eredetileg egyenes tengelyű, L hosszúságú elemet az ábrán látható módon körré
hajlítottuk úgy, hogy a kör sugara R = L / π értékű legyen (vagyis a lemez tengely irányú
hossza ne változzon). Az elem vastagsága t, az egyes metszetek állapotjellemzőinek
leírásához pedig még egy külön h lokális koordinátát is bevezettünk.
a./ Írjuk fel először a Lagrange-koordinátákat a sugár, a vastagságot jellemző h lokális-,
valamint egy ϕ polárkoordináta segítségével (lásd a jelöléseket a következő ábrán is):
.
Eredeti állapot
A-A metszet

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
X = R ϕ , Y = R + h
Eredeti állapot
A polárszög értéke és trigonometrikus függvénye a fentiek alapján:
X
ϕ = , innen:
R
X X
sin ϕ = sin , cos ϕ = cos .
R R
A megváltozott állapotot jellemző Euler-koordináták is számíthatók az ábra alapján:
x = R + h sin ϕ , y = R + h cos ϕ .
( ) ( )
A két koordinátarendszer elemeinek összekapcsolása:
X X
x = Y sin , y = Y cos .
R R
Egy tetszőleges pont eltolódásainak számítása 3 az előadáson tanultak alapján:
X x
u = x − X = Y sin − X , v = y − Y = Y cos − Y .
R R
Az eltolódások első deriváltjai:
∂u Y X ∂u
X
= cos − 1, = sin ,
∂X R R ∂Y
R
∂v Y X ∂v
X
= − sin , = cos −1.
∂X R R ∂Y
R
A Green-Lagrange-tenzor síkbeli esethez tartozó komponensei a behelyettesítés után:
( ) 2
2 2 2
∂u 1 ⎡⎛ ∂u ⎞ ⎛ ∂v
⎞ ⎤ 1 ⎛ R + h ⎞ h 1 ⎛ h ⎞
EXX
= + ⎢⎜ ⎟ + ⎜ ⎟ ⎥ = ⎜ − 1+
⎟ = +
2
⎜ ⎟
∂X 2 ⎢ X X 2 ⎜ R ⎟
⎣⎝ ∂ ⎠ ⎝ ∂ ⎠ ⎥⎦
R 2 R
⎝ ⎠ ⎝ ⎠
2 2
∂v 1 ⎡⎛ ∂u ⎞ ⎛ ∂v ⎞ ⎤
1 ⎛ ∂u ∂v ∂u ∂u ∂v ∂v
⎞
EY Y = + ⎢⎜ ⎟ + ⎜ ⎟ ⎥ = 0, EX
Y = ⎜ + + + ⎟ = 0.
∂Y 2 ⎢⎣ ⎝ ∂Y ⎠ ⎝ ∂Y ⎠ ⎥⎦
2 ⎝ ∂Y ∂X ∂X ∂Y ∂X ∂Y
⎠
E alakváltozás-komponens különbözik zérustól.
A számítás azt mutatja, hogy kizárólag az X X
Ennek értéke konstans a hossz mentén, zérus a középfelületen, továbbá nagysága egy adott
pont esetében alapvetően a középfelülettől mért távolságtól függ.
Megjegyezzük, hogy ennél a feladatnál az az érdekes helyzet fordult elő, hogy az eredményül
kapott alakváltozás viszonylag nem túl nagy, hiszen a vastagság lényegesen kisebb, mint a
sugár, de a számítás során kapott egyes komponensek viszont külön-külön igen jelentősek is
3 Jelen esetben w = 0, hiszen síkbeli feladatot vizsgálunk.
5
Megváltozott állapot

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
∂u ∂v
lehetnek. Például a középsíknál (Y = R esetén) számított első deriváltak közül és
∂X ∂ Y
nulla és -2 (!) között változhat, de a másik két derivált is igen nagy lehet: u ∂
nulla és egy,
∂ Y
∂v
pedig nulla és -1 közötti változhat.
∂X
Fontos emlékeztetnünk arra, hogy a Green-Lagrange-tenzor elemei közvetlenül nem
használhatók fel a megváltozott hosszak számítására, hiszen eredetileg hossznégyzetek
különbségének jellemzésére alkották meg őket, némi átalakítással azonban a „valódi”
hosszváltozás is meghatározható belőlük. Például ebben az „egydimenziós” feladatban (az
egyszerűség kedvéért indexek nélküli változókat használva) a Green-Lagrange-alakváltozás
az eredeti definíció alapján (itt l az új, l 0 pedig az eredeti hossza egy egydimenziós elemnek):
l − l
E = .
2 2
0
2
2l0
Ha (tetszőleges értékű nyúlásra) egy „hagyományos” mérnöki alakváltozást
l − l0
ε =
l0
módon definiálunk, akkor az első képletből kifejezett l értéket a másikba helyettesítve a
következőt kapjuk:
ε = 2E + 1 − 1.
Ennek segítségével már meghatározható az új hosszúság a kezdeti érték felhasználásával:
l = l 1+ ε = l 2E + 1 .
( )
0 0
Nézzünk ennek bemutatására egy numerikus példát az előbbi, hajlított lemezcsíkra kapott
eredmények felhasználásával. Legyen például L = 30 cm, R = L / π = 9,549297cm
, a
vastagság pedig: t = 2 mm. Számítsuk ki a Green-Lagrange-tenzor felhasználásával a
„külső”, domború felületrészhez (h = +1 mm) tartozó új hosszúságot. Maga a GLalakváltozás
az adott numerikus értékekkel:
2
h 1 ⎛ h ⎞
EXX
= + ⎜ ⎟
R 2 ⎝ R ⎠
A mérnöki alakváltozás:
1 1 ⎛ 1 ⎞
= +
95,49297 2
⎜
95, 49297
⎟
⎝ ⎠
= 1,05268 ⋅10
ε =
A külső felület új hossza:
−2
2E + 1 − 1 = 1,0472 ⋅ 10 .
l = L 1+ ε = L 2E + 1 = 303,14159 mm .
( )
Ez az érték könnyen ellenőrizhető, hiszen π -vel elosztott értékének egyeznie kell az eredeti
sugár +h-val megnövelt nagyságával:
l
= 96, 49297 mm
π
vagyis a számítás helyes volt.
⇔ R + h = 96,49297 mm ,
b./ Számítsuk ki most az Almansi-Hamel-féle alakváltozástenzort! Az előadáson tanult
definíció az Euler-koordináták segítségével:
1 1
1 ⎛ u
−T − ∂u ∂ i j ∂uk ∂u
⎞
k
e = ⎡I -F F , vagyindexes jelöléssel : ei
j
2 ⎣
⋅ ⎤
⎦
= ⎜ + − ⎟ .
2 ⎜ ∂x j ∂x i ∂x i ∂x
⎟
⎝ j ⎠
6
2
−2
.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
A tenzor meghatározáshoz először a Lagrange-koordinátákat kell kifejeznünk az Eulerváltozók
segítségével:
x
X = R ϕ = R arctg ,
y
Az elmozdulások Euler-koordinátákkal:
Y = R + h =
2 2
x + y .
x
u = x − X = x − R arctg ,
y
v = y − Y = y −
2 2
x + y .
A következő lépés a derivált függvények számítása:
∂ u
= 1− R
∂ x 1 +
1 1 Ry
= 1− 2 2 2
x / y y x + y
Ry
= 1 − , 2
( R + h)
( )
∂ u 1 ⎛ 1 ⎞ Rx Rx
= −R x⎜
− ⎟ = =
∂ y 1 + / ⎝ y ⎠ x + y ( R + h)
( x y)
2 2 2 2 2
∂ v 2x
x ∂ v 2y
y
= − = − , = 1− = 1 − .
∂ x 2 2
2 x + y R + h ∂ y 2 2
2 x + y R + h
A tenzor elemi részletesen:
2 2 2 2
∂u 1 ⎡⎛ ∂u ⎞ ⎛ ∂v
⎞ ⎤ 1 ⎡ 1 ⎛ R y 2 ⎞⎤
ex x = − ⎢⎜ ⎟ + ⎜ ⎟ ⎥ = ⎢1 − x ,
2 ⎜ + 2 ⎟⎥
∂x 2 ⎣⎢ ⎝ ∂x ⎠ ⎝ ∂ x ⎠ ⎦⎥
2 ⎣ ( R + h) ⎝ ( R + h)
⎠⎦
2 2
2 2
∂v 1 ⎡⎛ ∂u ⎞ ⎛ ∂v
⎞ ⎤ 1 ⎡ 1 ⎛ R x 2 ⎞⎤
ey y = − ⎢⎜ ⎟ + ⎜ ⎟ ⎥ = ⎢1 − y ,
2 ⎜ + 2 ⎟⎥
∂y 2 ⎢⎣ ⎝ ∂y ⎠ ⎝ ∂ y ⎠ ⎥⎦
2 ⎣ ( R + h) ⎝ ( R + h)
⎠⎦
2
1 ⎡∂u ∂v ⎛ ∂u ∂u ∂v ∂v
⎞⎤
xy ⎛ R ⎞
ex
y = ⎢ + − ⎜ + ⎟⎥
= 1 .
2 ⎜ − 2 ⎟
2 ⎣ ∂y ∂x ⎝ ∂x ∂y ∂x ∂ y ⎠⎦ 2( R + h) ⎝ ( R + h)
⎠
Ezek az alakváltozás-komponensek a középfelületen szintén zérus értékűek 4 .
Befejezésül hasonlítsuk össze a lemez egy középső metszetében lévő pontnál a kétféle
alakváltozástenzort! A sugár és a lokális koordináta: R = 100 mm, h = 1 mm.
A koordináták a kétféle rendszer szerint:
x = R + h, Az alakváltozás-tenzorok:
y = 0 ⇔ X = R π / 2, Y = R + h .
( ) 2
1 ⎡ R + h ⎤
EXX = ⎢− 1+ 0,01005, 2 ⎥ =
2 ⎢⎣ R ⎥⎦
EY Y = 0, EX
Y = 0,
2
1 ⎡ R ⎤
e x x = 0, e y y = ⎢1− 0,00985, e 0.
2 ⎥ = x y =
2 ⎣ ( R + h)
⎦
Az alakváltozás-tenzorok elemeinek értelmezését segíti a következő ábra:
4 Megjegyezzük, hogy az AH-tenzor használata esetén is megteremthető az 1D mérnöki
1
2 2 ε (1 + ε )
l −l0
alakváltozással a kapcsolat: e = = 2 .
2 2 2
2 l (1 + ε
)
7
,

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
e yy e yx
RAJZOLÓ: ε HELYETT e − t!!!!
e
xy
e xx
2.2. Hivatkozva az első gyakorlat 2.1-es példájára, számítsuk ki a kétdimenziós jobb és
bal Cauchy-Green-tenzorokat!
Emlékeztetőül a 2.1-es példához tartozó ábra:
Mivel az ottani példában már kiszámítottuk
a gradiens-tenzort:
1 ⎡2 F =
2
⎢
⎣0 3⎤
3
⎥
⎦ ,
a két keresett tenzor egyszerűen számítható
a hozzájuk tartozó definícióból. A jobb
Cauchy-Green-tenzor:
C =
1 ⎡ T 2
F F = ⎢
2 ⎢
⎣3 3⎤
⎥ .
9⎥
⎦
A másik keresett deformációs-tenzor, a bal Cauchy-Green (vagy Finger-féle) változat:
T 1 ⎡13 b = F F =
4
⎢
⎣ 9
9⎤
.
9
⎥
⎦
Megjegyezzük, hogy ezen tenzorok segítségével egy adott feladatnál egyszerűen számíthatók
a Green-Lagrange- és az Almansi-Hamel-féle alakváltozástenzorok is:
1 1 0
E ( C I )
2 4 3
3 1 1 1 0
, e ( I b )
7 2 18 9
9
.
4
−
⎡
= − = ⎢
⎣
⎤ ⎡
⎥ = − = ⎢
⎦ ⎣
⎤
−
⎥
⎦
A 2.1-es példában már meghatározott
1 ⎡2 e2 = F E 2 =
2
⎢
⎣0 3⎤ ⎡0⎤ ⎡1,5 ⎤
=
3
⎥ ⎢
1
⎥ ⎢
1,5
⎥
⎦ ⎣ ⎦ ⎣ ⎦ vektor
hossznégyzetének vizsgálatára például felhasználhatjuk a GL-tenzort. Az eredeti definíció
alapján (figyelembe véve, hogy az új hossz
vizsgálatánál a következőt kapjuk:
4,5 , az eredeti pedig 1) ennek a vektornak a
2 2
1 ⎛ l − L ⎞ 7
EGL,
e = 2 ⎜ 2 ⎟ = .
2 ⎝ L ⎠ 4
8

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
Használjuk most a GL-tenzort ugyanennek a számításnak a végrehajtására (ilyenkor az e2 -t
az eredeti Lagrange-rendszerben adott koordinátáival, vagyis egy ott egységvektorként adott
változóként kell figyelembe vennünk):
T
1 ⎡0 3⎤ ⎡0⎤ 7
EGL, e = E [ ]
2 2 EE 2 = 0 1
4
⎢
3 7
⎥ ⎢ =
1
⎥ .
⎣ ⎦ ⎣ ⎦ 4
A számítás „fordított” sorrendben is elvégezhető. Ugyanennek a vektornak az Eulerrendszerből
a Lagrange-rendszerbe történő transzformálásánál a hossznégyzet változása:
2 2
1 ⎛ l − L ⎞ 7
eAH
, e = 2 ⎜ 2 ⎟ =
2 ⎝ l ⎠ 18
módon számítható, ami szintén egyezik az Almansi-Hamel-féle tenzorral történő
transzformációval:
⎡ 1 ⎤
T ⎡ 1 1 ⎤ 1 ⎡0 9 ⎤ ⎢ ⎥
7
eAH , e = e
2 2 ee2
= ⎢ ⎥
2 2 18
⎢ ⎢ ⎥ =
9 4
⎥ .
⎣ ⎦ ⎣ − ⎦ ⎢ 1 ⎥ 18
⎢
⎣ 2
⎥
⎦
3. Az alakváltozás-sebesség tenzor (D)
3.1. Számítsuk ki az AH-tenzor anyagi idő szerinti deriváltját az alakváltozás-sebesség
tenzor segítségével!
A tenzor számítása az eredeti definíció alapján:
1 −T −1
e = ⎡ ⋅ ⎤
2 ⎣
I -F F
⎦
.
Az anyagi idő szerinti derivált ennek figyelembevételével:
1 D −T −1 1 ⎛ D −T −1 −T D −1
⎞
eɺ = − ( F ⋅ F ) = − ⎜ ( F ) ⋅ F + F ⋅ ( F ) ⎟ .
2 Dt 2 ⎝ Dt Dt ⎠
Figyelembe véve, hogy a sebesség-gradiens tenzor az alábbi módon számítható (lásd a
második hét előadásvázlatát):
1
L F F −
= ɺ ⋅ ,
az előbbi egyenletben szereplő deriváltak az alábbiak lesznek:
D −1 −1 −1 −1 −1
( F ) = − F Fɺ F = −F L ⇐F
F= I azonosságból kiindulva, láncszabállyal ,
Dt
D −T −T D T −T T −T −T
T
( F ) = − F ( F ) F = −L F ⇐ F F = I azonosságból kiindulva, láncszabállyal .
Dt Dt
Helyettesítsük vissza ezeket a deriváltakat az AH-tenzor deriváltjának képletébe, így ott most
már megjelenik a sebesség-gradiens tenzor szimmetrikus részét jelentő alakváltozás-sebesség
tenzor:
1 T −T −1 −T −1
1 T T
eɺ = − ( −L F F − F F L) = ⎡ ( − 2 ) + ( − 2 ⎤ = − −
2 2 ⎣
L I e I e)L
⎦
D L e eL .
4. Az F gradienstenzor szorzat alakú (poláris) felbontása
Emlékeztetőül a poláris felbontás alapvető képletei:
F = R U ,
U = F F R = F U
⋅ ahol ( ) 1
9
T 2 -1
⋅ , ⋅
.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
A poláris felbontás mechanikai értelmezését illusztrálja a következő ábra, ahol a felbontás
elméletileg lehetséges, másik sorrendű változatát is feltüntettük (ezt most nem fogjuk
használni):
Eredeti helyzet
Emlékeztetőül megjegyezzük, hogy egy mátrix négyzetgyökének kiszámításához az alábbi
lépések szükségesek:
T
a./ Határozzuk meg az F ⋅ F mátrix sajátértékeit és sajátvektorait.
b./ A λ i sajátértékeknek vegyük a négyzetgyökét s helyezzük el őket egy diagonál mátrixba:
H = λ1 , λ 2 , λ 3 .
c./ A sajátvektorokat oszloponként helyezzük el egy A mátrixba.
T T
U = F ⋅F = A ⋅H ⋅ A .
d./ A nyúlási tenzor ezek segítségével: ( ) 1
2
4.1. Az alábbi kétdimenziós feladatban adottak a mozgásegyenletek. Határozzuk meg a
gradienstenzort és poláris felbontását a t = 1 időpillanatban az X = 0 helyen!
Az Euler- és Lagrange-koordináták közötti változást leíró egyenletek az idő függvényében:
1 1
x = ( 4X + ( 9 − 3X − 5 Y − XY ) t) , y = ( 4Y + ( 16 + 8X
) t)
.
4 4
A gradiens-tenzor:
⎡ ∂x ⎢∂X F = ⎢
⎢ ∂y ⎢⎣ ∂X ∂x
⎤
∂Y
⎥ 1 ⎡1 ⎥ =
∂y 4
⎢
⎥ ⎣8 ∂Y
⎥⎦
−5⎤
4
⎥ .
⎦
T
Az F ⋅F szorzat:
1 ⎡65 16
⎢
⎣27 27⎤ ⎡4,0625 41
⎥ = ⎢
⎦ ⎣1,6875 1,6875 ⎤
2,5625
⎥
⎦ .
A karakterisztikus egyenlet és a sajátértékek:
4,0625 − λ
1,6875
1,6875
2
= 0 ⇒ λ − 6,625λ + 7,5623 = 0 ⇒ λ 1 = 5,1592,
2,5625 − λ
λ 2 = 1,4658 .
10
Deformálódott állapot

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
A sajátértékek négyzetgyökéből alkotott diagonálmátrix:
⎡2,2714 0 ⎤
H = ⎢
0 1, 2107
⎥
⎣ ⎦ .
A sajátvektorok meghatározása következik (csak az első vektorra mutatjuk be a számítás
részleteit, a másiknál teljesen hasonlóak a lépések). A szükséges egyenletek (a
sajátértékfeladat első egyenletébe visszahelyettesített első sajátérték felhasználásával illetve
az iránykoszinuszok négyzetösszegére vonatkozó feltételből):
2 2
(4,0625 − 5,1592) n + 1,6875 n = 0, n + n = 1.
T
Az első sajátvektor: [ ]
1x 1y 1x 1y
a 1 = 0,8385 0,5449 .
T
A második sajátvektor: a 2 = [ − 0,5449
⎡0,8385 0,8385]
. Az A tenzor: A = ⎢
⎣0,5449 −0,5449⎤
0,8385
⎥
⎦ .
T ⎡1,9564 Az U nyúlási tenzor: U = A ⋅ H ⋅ A = U = ⎢
⎣0,4846 0,4846⎤
1,5257
⎥ .
⎦
Utolsó lépésként az R rotációs tenzor meghatározása következik:
-1
1 ⎡1 R = F⋅ U = R =
4
⎢
⎣8 −5⎤ 1 ⎡ 1,5257
4
⎥
2,75
⎢
⎦ ⎣−0, 4846
−0,4846⎤ ⎡0,3590 =
1,9564
⎥ ⎢
⎦ ⎣0,9333 −0,9333⎤
0,3590
⎥
⎦ .
Az eredmények ellenőrzését a triviálisan adódó RU szorzat mellett másképpen is
végrehajthatjuk, például úgy, hogy egyúttal megmutatjuk az egyes komponensek fizikai
tartalmát.
Transzformáljuk például a sajátvektorokat az anyagi térből az Euler-rendszerbe a gradienstenzor
segítségével:
E 1 ⎡1 −5⎤ ⎡0,8385⎤ ⎡−0,4715⎤ E 1 ⎡1 −5⎤ ⎡−0,5449⎤ ⎡ −1,1843
⎤
a1 = F a1 = , a2 F a2
.
4
⎢
8 4
⎥ ⎢
0,5449
⎥ = ⎢ = = =
2,2219
⎥
4
⎢
8 4
⎥ ⎢
0,8385
⎥ ⎢
−0,2513
⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦
Az új vektorok természetesen most is merőlegesek egymásra, skalár szorzatuk zérus. Állítsuk
elő ugyanezt a transzformációt a poláris szorzat segítségével. Első lépésként szorozzuk be a
két eredeti sajátvektort a sajátértékekből adódó, nyújtást jellemző értékkel:
⎡0,8385⎤ ⎡1,9046 ⎤ ⎡ −0,5449 ⎤ ⎡−0,6597 ⎤
λ 1 a1 = 2, 2714 ⎢ , 2 a2
2,2714 ,
0,5449
⎥ = ⎢ λ = =
1,2377
⎥ ⎢
0,8385
⎥ ⎢
1,0152
⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦
majd ezeket a vektorokat a rotációs tenzor segítségével transzformáljuk az Euler-rendszerbe:
E
⎡0,3590 −0,9333⎤ ⎡1,9046⎤ ⎡−0,4715 ⎤
a1 = R λ 1 a1
= ⎢ ,
0,9333 0,3590
⎥ ⎢
1, 2377
⎥ = ⎢
2, 2219
⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
E
⎡0,3590 −0,9333⎤ ⎡−0,6597⎤ ⎡ −1,1843
⎤
a2 = R λ 2 a2
= ⎢ .
0,9333 0,3590
⎥ ⎢ =
1,0152
⎥ ⎢
−0,2513
⎥
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
Az eredmények megegyeznek az F tenzor használatával kapott korábbi transzformációval,
tehát a poláris felbontás helyes volt.
5. Főnyúlások számítása
5.1. Egy homogén térbeli alakváltozási állapotú testnél határozzuk meg a főnyúlások és
a hozzájuk tartozó főirányok értékeit!
Az ábrán látható testnél a terhelés előtti méreteket tüntettük fel. Feltételezzük, hogy az
alakváltozási állapot az egész testben homogén, és az alábbi GL-tenzor jellemzi:
11

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
⎡−3,72000 −2,57801 −3,89094⎤
E =
⎢
8,04615 1,01118
⎥
⎢
−
⎥
10
⎢⎣ szimm.
4,67385 ⎥⎦
Az előadáson láttuk, hogy az alakváltozás-tenzorok hoz tartozó sajátértékfeladat
karakterisztikus egyenletének alakja a következő 5 3 2
: − λ + I′ λ − I′ λ + I′
= .
12
−3
.
1 2 3 0
Az együtthatók az alakváltozás-tenzor invariánsai (az egyszerűség kedvéért kiemeljük a
3
10 − értékű tagot):
I′ = E + E + E = − 3,72000 + 8,04615 + 4,67385 = 9,00000,
I
1 11 22 33
E E E E E E
8,04615 −1,01118 −3,72000 −3,89094
22 23 11 13 11 12
′ 2 = + + = + +
E32 E 33 E 31 E33 E21 E 22 −1,01118 4,67385 −3,89094
4,67385
−3,72000 −2,57801
+ = − 32,51994,
−2,57801
8,04615
I
′3
−3,72000 −2,57801 −3,89094
= 8,04615 − 1,01118 = − 309, 255562.
szimm.
4,67385
Behelyettesítve a karakterisztikus egyenletbe:
3 2
− λ + 9λ + 32,51994λ − 309, 25562= 0 .
A harmadfokú egyenlet megoldásából (Cardano-képlet, Newton-Raphson-módszer, stb.) az
3
alábbi három gyököt kapjuk (visszaírjuk 10 − -at):
−3 −3 −3
λ = E = 8,6 ⋅10 , λ = E = 6, 2⋅10 , λ = E = −5,8 ⋅ 10 .
1 1 2 2 3 3
5
Megjegyezzük, hogy az alakváltozási tenzor invariánsait szokás vesszős felső indexszel ellátni,
megkülönböztetésül a feszültségi tenzor invariánsaitól, amelyek vessző nélküliek. Ennek a jelölési
módnak elsősorban anyagmodelleknél van jelentősége, ahol előfordul mindkét változórendszer
együttes alkalmazása.
Egy másik megjegyzés arra vonatkozik, hogy sok könyv, cikk, stb. a fenti karakterisztikus
3 2
egyenletnek –1-gyel megszorzott alakját használja ( 1 2 3 0
λ − I′ λ + I′ λ − I′
= ). Ennek a végeredmény
szempontjából természetesen nincs jelentősége.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
Ezek a gyökök a tenzor sajátértékei, mechanikai tartalmukat tekintve ezek a GL-tenzorhoz
tartozó főnyúlások.
A főirányok számítása a sajátvektorok meghatározását jelenti. Az első sajátvektor számítását
a sajátértékfeladat első két egyenletének, illetve az egységvektorok iránykoszinuszaira
vonatkozó összefüggés segítségével hajtjuk végre:
(1) (1) (1)
−3,72 −8,6 n − 2,57801n − 3,89094 n = 0,
( )
(1) (1) (1)
( n1 ) ( n2 ) ( n3
)
1 2 3
( )
− 2,57801n + 8,04615 −8,6 n − 1,01118 n = 0,
(1) (1) (1)
1 2 3
2 2 2
+ + = 1.
Megjegyezzük, hogy ennél a nemlineáris egyenletrendszernél gyakran alkalmazzák azt a
(1)
technikát, hogy az egyik komponenst egységnyinek tekintik (legyen például most n 1 = 1,0 ),
és akkor már csak egy kétismeretlenes lineáris egyenletrendszert kell megoldani 6 :
(1) (1)
−12,32 ⋅1− 2,57801n − 3,89094 n = 0,
13
2 3
(1) (1)
−2,57801⋅1 − 0,55385 n2 − 1,01118 n3
Az egyes komponensek:
= 0.
(1)
n1 = 1,0
(1)
n2 = − 5,37111
(1)
n3
= 0,39239 .
Az egységvektorrá történő átalakításhoz meghatározzuk ennek a vektornak a hosszát:
(1) 2 2 2
n = 1 + 5,37111 + 0,39239 = 5, 47748.
A végleges normált első sajátvektor:
T
n 1 = [ 0,1826 − 0,9806 0,0716]
.
A második sajátvektor számításához a második sajátértéket (főnyúlást) használjuk fel:
−3,72 − 6,2
(2) (2) (2)
n − 2,57801n − 3,89094 n = 0,
( )
1 2 3
( )
(2) (2) (2)
− 2,57801n 1 + 8,04615 − 6,2 n2 − 1,01118 n3
= 0.
Legyen most is például az első iránykoszinusz értéke egységnyi:
(2) (2)
n1 → n1
= 1,
így a kétismeretlenes lineáris egyenletrendszerünk:
(2) (2)
−9,92 ⋅1− 2,57801n − 3,89094 n = 0,
A megoldás:
A vektor hossza:
2 3
−2,57801⋅ 1+ 1,84615 n − 1,01118 n = 0.
(2) (2) (2)
1 2 3
(2) (2)
2 3
n = 1,0 n = 0,0 n = − 2,54951 .
(2) 2 2 2
n = 1 + 0,0 + 2,54951 = 2,73862
A második főirány normált vektora:
T
n 2 = [ 0,3651 0,0 − 0,9309]
.
A harmadik főirány meghatározása ugyanilyen lépésekkel történik. Megadjuk a
részeredményeket (most is az első komponenst választottuk egységnyinek az
egyenletrendszer megoldásánál):
6 Ennél a fajta megoldásnál vigyázni kell arra, nehogy az egységnyire felvett komponens véletlenül
merőleges legyen a végleges sajátvektor síkjára (ilyenkor rossz megoldást ad ez a módszer).

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
n = 1,0 n = 0, 21483 n = 0,39223 ,
(3) (2) (2)
1 2 3
T
[ ]
14
(3) 2 2 2
n = 1 + 0, 21483 + 0,39223 = 1,09545 .
n 3 = 0,9129 0,1961 0,3581 .
Megjegyezzük, hogy a harmadik főirányt az előző kettő vektoriális szorzata segítségével is
kiszámíthatjuk.
5.2. Határozzuk meg egy sík feszültségi állapotban lévő tárcsa egy adott pontjához
tartozó jobb Cauchy-tenzor főnyúlásait. A deformációgradiens-tenzor adott.
A gradiens-tenzor:
A jobb Cauchy-tenzor:
A sajátértékfeladat:
A karakterisztikus egyenlet:
A főnyúlások:
⎡3 −1
0⎤
F =
⎢
2 2 0
⎥
⎢ ⎥
,
⎢⎣ 0 0 1⎥⎦
⎡13 1 0⎤
T
C = F F =
⎢
1 5 0
⎥
⎢ ⎥
.
⎢⎣ 0 0 1⎥⎦
⎡
⎣C I ⎤
⎦
2
13 − λ 1 0
2 2
det − λ = 1 5 − λ 0
2
0 0 1−
λ
2 4 2
( λ )( λ λ )
1− − 18 + 64 = 0.
λ = 9 ± 17, λ = 1.
2 2
1,2 3
A sajátvektorok:
T
n = 0,993 0,122 0 ,
T
n = − 0,122 0,933 0 ,
T
n = 0 0 1 .
[ ] [ ] [ ]
1 2 1
Megjegyezzük, hogy a főnyúlások és a sajátvektorok segítségével most már egyszerűen
meghatározhatjuk F poláris felbontásához tartozó R és U tenzorokat:
⎡ 3,6 0,17 0⎤
T T T
U = C = λ1n 1n1 + λ2 n2 n2 + λ3n
3n 3 =
⎢
0,17 2, 23 0
⎥
⎢ ⎥
,
⎢⎣ 0 0 1⎥⎦
illetve
0,86 0,51 0
1
R FU 0,51 0,86 0 .
0 0 1
−
⎡ − ⎤
= =
⎢
−
⎥
⎢ ⎥
⎢⎣ ⎥⎦
Jelen esetben R másképpen is számítható, ha kihasználjuk a sík feszültségi állapotot, hiszen
ilyenkor
⎡ cosθ sinθ 0⎤
R =
⎢
sinθ cosθ 0
⎥
⎢
−
⎥
.
⎢⎣ 0 0 1⎥⎦
Ha kihasználjuk az
.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
−1
R = R és U = R F, U = U
T T T
összefüggéseket, akkor felírható az alábbi feltételi egyenlet:
U12 = R11F12 + R21F22 = R12 F11 + R22F21 = U 21 .
Innen az ismeretlen szög meghatározható:
F12 − F21
�
tgθ
= ⇒ θ = −31,0
F + F
11 22
5.3. Bontsunk fel egy gradiens-tenzor szorzat alakban deviátoros és gömbi részre úgy,
hogy alkalmazható legyen rugalmasan összenyomhatatlan anyagok vizsgálatára!
A számítás során a harmadik előadás 3.12-es összefüggését fogjuk használni:
d
g
15
1 1
3 3
d .
F Fg
F , ⋅ = ahol F J I , F J F
−
= =
Legyen például a gradiens-tenzor az alábbi:
⎡3 −1
0⎤
F =
⎢
2 2 0
⎥
⎢ ⎥
.
⎢⎣ 0 0 1⎥⎦
A tenzor determinánsa:
J = F = 8 .
Ennek megfelelően a két komponens:
⎡2 0 0⎤ ⎡1,5 −0,5
0 ⎤
1/3 −1/3
J = 2, J = 0,5, F =
⎢
0 2 0
⎥
, F
⎢
1 1 0
⎥
g ⎢ ⎥
=
dev ⎢ ⎥
.
⎢⎣ 0 0 2⎥⎦ ⎢⎣ 0 0 0,5⎥⎦
Ellenőrizhető, hogy a két tenzor szorzata megadja az eredeti gradiens-tenzort, továbbá a
deviátoros rész determinánsa egységnyi ( 1
dev )
F = .
Rugalmasan összenyomhatatlan anyagoknál a deviátoros részt szokás felhasználni a
módosított alakváltozási vagy nyúlási tenzorok számítására, így például a módosított jobb
Cauchy-tenzor ilyen esetben:
ˆ T −2/3 T −2/3
C = F F = J F F = J C .
dev dev
5.4. Határozzuk meg az 5.1-es példában szereplő AG szakasz hosszváltozását!
Számítsuk ki először a két pontot összekötő egyeneshez tartozó vektorokat:
T
AG
[ ] 2 2 2
r = 50 100 70 , r = 50 + 100 + 70 = 131,91 cm .
Az irány egységvektora:
n = 0,37905 0,75810 0,53067 .
T
AG
[ ]
Egy adott irányhoz tartozó GL-alakváltozást az X,Y,Z bázisban megadott GL-tenzor
transzformálásával tudjuk meghatározni. Most nem kell az egész tenzort transzformálnunk,
elegendő csak az AG szakasz irányának megfelelő „metszetet” előállítanunk:

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
AG
T
AG AG
E = n En =
⎡−3,72000 −2,57801 −3,89094⎤
⎡0,37095⎤ −3
= [ 0,37905 0,75810 0,53067
⎢
] 2,57801 8,04615 1,01118
⎥ ⎢
0,75810
⎥
⎢
− −
⎥ ⎢ ⎥
10 =
⎢⎣ −3,89094 −1,01118
4,67385 ⎥⎦ ⎢⎣ 0,53067⎥⎦
−3
= 1,54541⋅ 10
Ennek az értéknek a segítségével az 1D vizsgálatoknál szokásos alakváltozás is kiszámítható
(lásd a második hét gyakorlatának 2.1-es példáját):
ag − AG
−3 −3
ε AG = = 1+ 2EAG − 1 = 1+ 21,54541⋅ 10 − 1 = 1,54422 ⋅ 10 .
AG
Az új átló értéke ennek segítségével:
−3
ag = AG ⋅ 1+ ε = 131,91 1+ 1,54422 ⋅ 10 = 132,11 cm .
( AG ) ( )
5.5. Határozzuk meg az ábrán látható sík alakváltozási állapothoz tartozó alakváltozásjellemzőket
(elforgatott rendszerhez tartozó értékek, főnyúlások)!
Az ábrán látható alakváltozás-komponensek most kis alakváltozásokat jelentenek. Számítsuk
ki első lépésként az x-y rendszerhez képest 35 fokkal elforgatott új x′ − y′
bázisban az
alakváltozásokat (lásd a következő ábrát)!
16

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
Kétdimenziós esetben az általános transzformáló összefüggések egyszerű skalár
kifejezésekkel is megadhatók, a gyakorlatban többnyire ezeket használják. Ilyenkor
trigonometriai átalakításokkal a kétszeres szögeket használják:
1 1
ε ′ x x = ( ε x x + ε yy ) + ( εx x − ε yy ) cos 2ϑ + εx y sin 2 ϑ,
2 2
1 1
ε ′ y y = ( ε x x + ε yy ) − ( εx x − ε yy ) cos 2ϑ − εx y sin 2 ϑ,
2 2
1
ε ′ x y = − ( εx x − ε yy ) sin 2ϑ + εx y cos 2 ϑ.
2
Behelyettesítve a megadott értékeket:
−3 ⎧1 1
� � ⎫
−3
ε ′ x x = 10 ⎨ ( − 0,75 + 0,5) + ( −0,75 − 0,5) cos70 − 0, 4sin 70 ⎬ = −0,7146 ⋅10
,
⎩2 2
⎭
−3 ⎧1 1
� � ⎫
−3
ε ′ y y = 10 ⎨ ( − 0,75 + 0,5) − ( −0,75 − 0,5) cos 70 + 0,4sin 70 ⎬ = 0, 4646⋅10 ,
⎩2 2
⎭
−3 ⎧ 1
� � ⎫
−3
ε ′ x y = 10 ⎨− ( −0,75 − 0,5) sin 70 − 0,4cos70 ⎬ = 0,4505 ⋅10
.
⎩ 2
⎭
A transzformáció helyessége a két különböző rendszerben számított alakváltozási
invariánsok összehasonlításával ellenőrizhető:
I′
( ε ) = ε + ε = − 0,00075 + 0,0005 = −0,00025,
1
x x y y
I′
( ε ′ ) = ε ′ + ε ′ = − 0,0007146 + 0,0004646 = −0,00025,
1
x x y y
ε ε −0,00075 −0,0004
I′
ε = = = − ⋅
x x x y
−7
2(
) 5,35 10 ,
ε y x ε y y −0,0004
0,0005
I′
′
ε′ ε′ −0,0007146
0,0004505
x x x y
−7
2(
ε ) = = = − 5,35 ⋅10
,
ε′ y x ε′
y y 0,0004505 0,0004646
A harmadik invariáns sík feladatok esetében mindig zérus.
Határozzuk meg ezek után a főnyúlások értékeit.
Kétdimenziós esetben a sajátértékfeladat karakterisztikus egyenlete másodfokú, így az ismert
megoldóképlet segítségével számíthatók a főnyúlások. A helyes indexszelésnél mindig
figyelembe kell vennünk, hogy most az eredeti másodrendű alakváltozás-mátrix egy sora és
egy oszlopa zérus, így minden esetben van egy darab zérusértékű főnyúlás. Ennek indexét a
sík feladatnál kapott eredmények előjelének figyelembevételével kell megadni.
A sík alakváltozási állapotnál alkalmazott megoldóképlet:
ε x x + ε y y
ε 1,3 = ±
2
2
⎛ εx x − ε y y ⎞ ⎧
2 −3
⎪− 0,75 + 0,5
⎜ ⎟ + εx y ⇒ε 1,3 = 10 ⎨ ±
⎝ 2 ⎠ ⎪ 2
⎩
2
⎛ −0,75 − 0,5 ⎞
⎫
2 ⎪
⎜ ⎟ + ( −0,
4)
⎬
⎝ 2 ⎠ ⎪⎭
A zérus érték figyelembevételével a főnyúlások:
−3 ε 1 = 0,617 ⋅10 , ε 2 = 0,
−3
ε 3 = −0,867 ⋅ 10 .
Ebben az esetben a fő-szögtorzulások értéke mindig zérus.
Az invariánsokat újból felhasználhatjuk ellenőrzésre:
I′
( ε ) = ε + ε + ε = 0,000617 + 0 − 0,000867 = −0,00025,
1 i 1 2 3
17
( )
I′
ε = ε ε + ε ε + ε ε = ⋅ − = − ⋅
−7
2( i ) 1 3 1 2 2 3 0,000617 0,000867 5,35 10 .

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
A főirányok meghatározás is lényegesen egyszerűbb sík alakváltozási állapot esetén:
2εx y
2( −0,0004)
tg2α i = ⇒ tg2α
i = = 0,64 ⇒ α 1 = 106,31 , α 3 = 16,31
ε − ε −0,00075 − 0,0005
x x y y
18
� � .
A feladat befejezéseként megmutatjuk az alakváltozások Mohr-féle grafikus ábrázolását is,
az eredeti tenzor elemeinek illetve a főnyúlásoknak a feltüntetésével.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
6. Műveletek alakváltozástenzorokkal
6.1. Vizsgáljuk meg az ábrán látható, deformálódott négyzet különböző
alakváltozásjellemzőit!
Az ábrán látható 2D cellának feltüntettük kezdeti, és egy pillanatnyi helyzethez tartozó
állapotát.
Megadjuk a mozgásegyenleteket is, de mivel most csak egy t = konstans állapot vizsgálatát
fogjuk elvégezni, ezért az x = Φ ( X, t)
kapcsolati egyenletet egy rögzített, a további vizsgálat
számára közömbös nagyságú időérték behelyettesítésével írjuk fel. A vizsgált állapotnál ezek
az egyenletek a következők:
x = 1+ 1,01X + 0,03 Y, y = 2 + 0,02 X + 1,04 Y, z = Z .
Ennek inverz változata:
4900 5200 150 10000 100 5050
X = − + x − y, Y = − − x + y, Z = z .
5249 5249 5249 5249 5249 5249
A további vizsgálatok céljára fontos pontok kezdeti és pillanatnyi koordinátáit gyűjtsük ki
egy külön táblázatba:
Vizsgálandó pontok: X x
A(0,0 – 0,0) a(1,00 – 2,00)
B(1,0 – 0,0) b(2,01 – 2,02)
C(0,0 – 1,0) c(1,03 – 3,04)
D(1,0 – 1,0) d(2,04 – 3,06)
E(0,5 – 1,0) e(1,535 – 3,05)
F(107/202 – 0,0) f(1,535 – 20307/10100)
a./ Első lépésként számítsuk ki a deformált cellánál az egyes szakaszok új hosszát elemi
koordináta-geometriai összefüggések segítségével, az alakváltozás-tenzorok alkalmazása
nélkül! Ehhez a számításhoz a következő vektorokra lesz szükségünk:
19

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
⎡1,01⎤ r ab = ⎢
0,02
⎥
⎣ ⎦
⇒ r ab =
2 2
1,01 + 0,02 = 1,010198,
⎡0,03⎤ r ac = ⎢
1,04
⎥
⎣ ⎦
⇒ r ac =
2 2
0,03 + 1,04 = 1,0404326,
⎡1,04 ⎤
r ad = ⎢
1,06
⎥
⎣ ⎦
⇒ r a d =
2 2
1,04 + 1,06 = 1,4849916,
⎡ 0,00 ⎤
r e f = ⎢
1,039406
⎥
⎣− ⎦
⇒ r e f =
2 2
0,0 + ( − 1,039406) = 1,039406,
⎡0,029703⎤ r E F = ⎢
1,0
⎥
⎣ − ⎦
⇒ r E F =
2 2
0,029703 + ( − 1,0) = 1,000441.
Számítsuk ki a cab pontok által meghatározott szöget is:
cos ϕ c ab =
r ab ⋅r ac
r r
1,01 ⋅ 0,03 + 0,02 ⋅1,04
�
= = 0,048618375 ⇒ ϕ cab = 87, 213274 .
1,010198 ⋅1,0404326
ab ac
Mivel a kezdeti és pillanatnyi állapotok közötti összefüggéseket lineáris kapcsolati
egyenletekkel adtuk meg, a vektorok segítségével kapott eredményeink pontosak.
b./ Folytassuk most a számítást a Lagrange-bázis felhasználásával, a GL-tenzor
kiszámításával! Ehhez először az eltolódásfüggvények meghatározására lesz szükségünk:
u = x − X , v = y − Y, w = z − Z,
így :
u( X , Y, Z) = (1+ 1,01 X + 0,03 Y ) − X = 1+ 0,01X + 0,03 Y,
v = ( X , Y, Z) = (2 + 0,02 X + 1,04 Y ) − Y = 2 + 0,02 X + 0,04 Y,
w = ( X , Y, Z) = Z − Z = 0.
Most már számíthatók a GL-tenzorhoz szükséges deriváltak. Először külön megadjuk a
lineáris tagokat, hiszen ezek segítségével a kis alakváltozásokhoz szükséges tenzor már
felépíthető:
∂u = 0,01,
∂X ∂u = 0,03,
∂Y ∂v = 0,02,
∂X ∂v
= 0,04 ⇒
∂Y
⇒ ε x x = 0,01, ε y y = 0,04,
1
ε x y = ( 0,03 + 0,02) = 0,025.
2
A nagy alakváltozásokat jellemző GL-tenzor elemei:
1 2 2 2 1 2 2 2
EX X = 0,01 + ( 0,01 + 0,02 + 0 ) = 0,01025, EY
Y = 0,04 + ( 0,03 + 0,04 + 0 ) = 0,04125,
2 2
1
EX
Y = ( 0,03 + 0,02 + 0,01⋅ 0,03 + 0,02 ⋅ 0,04 + 0⋅ 0) = 0,02555.
2
A GL-tenzor segítségével – a korábbi példákban már alkalmazott módszerrel azonos módon
számíthatók egyes oldalélek megnyúlásai. Ilyenkor mindig az 1D fizikai alakváltozásokra
alkalmazott összefüggésekkel dolgozunk, így például X irányban:
fiz.
l − L r ab − r AB
ε X = 1+ 2EX X − 1 = = .
L r
20
AB

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
Innen r ab (vagyis a megváltozott hosszúságú oldalél) értéke:
r = 1+ 2E ⋅ r = 1+ 2⋅ 0,01025 ⋅ 1,0 = 1,010198 .
ab X X AB
Ez az érték pontosan megegyezik az előzőekben – koordinátageometriai úton számított –
értékekkel.
Hasonlóan számítható r ac nagysága is:
fiz.
l − L r ac − r AC
ε Y = 1+ 2EY Y − 1 = = ⇒
L r
AC
r = 1+ 2E ⋅ r = 1+ 2⋅ 0,04125 ⋅ 1,0 = 1,0404326.
ac Y Y AC
Ez az érték is azonos a korábban számítottal.
Fontos megjegyeznünk, hogy a GL-tenzor segítségével eddig számított két érték olyan
oldalélekre vonatkozott, melyek eredeti iránya megegyezett az X, illetve az Y koordinátatengelyekével!
Minden más esetben először magát a GL-tenzort kell transzformálnunk a
keresett irányba és csak utána hajthatók végre az itt alkalmazott eljárás lépései.
Ugyancsak hibás az a gondolkodásmód, amely például az ad átló (új) hosszát a most
számított ab és ac szakaszhosszak felhasználásával Pithagorász-tétellel kívánná
meghatározni:
2 2 2
r = r + r ⇒ r = r + r = + =
a d ab ac a d ab ac
21
2 2
1,010198 1,0404326 1,4501724
Összehasonlítva az adott szakasz hosszára korábban kapott eredménnyel, látható, hogy ez az
érték hibás!
A helyes számításhoz a GL-tenzor elemeit transzformálnunk kell a keresett irányba, jelen
esetben az AD átló által megadott tengely irányába (ennek megfelelően a transzformáció
szöge 45 fok):
1 1
EX ′ X ′ = ( EX X + EY Y ) + ( EX X − EY Y ) cos 2α + EX
Y sin 2α
=
2 2
1 1
� �
= ( 0,01025 + 0,04125) + ( 0,01025 − 0,04125) cos90 + 0,02555sin 90 = 0,0513
2 2
Ennek felhasználásával már alkalmazható az előző technika:
fiz.
l − L r a d − r AD
ε X ′ = 1+ 2EX ′ X ′ − 1 = = ⇒
L r
AD
r = 1+ 2E ⋅ r = 1+ 2⋅ 0,0513 ⋅ 2 = 1, 4849916.
a d X ′ X ′ AD
Ez már pontosan megegyezik a legelőször számított szakaszhosszal. 7
A két (koordináta-tengelyekkel eredetileg párhuzamos) oldal által meghatározott új szög is
számítható az új értékekből:
2E
fiz.
12
cos ϕ = ⇒
1+ 2E 1+ 2E
11 22
2E 2⋅ 0,02555
fiz.
X Y
cos ϕ c ab = = = 0,048618375.
1+ 2E 1+ 2E 1+ 2⋅ 0,01025 1+ 2⋅ 0,04125
X X Y Y
7 Az eltérés a pontos és a Pithagorász-tétellel számított hossz között közel 50 %-os, ezért durva hibát
követünk el, ha nem a pontos eljárást alkalmazzuk.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
A számítás most is pontosan egyezik a korábbival.
Érdekes megvizsgálnunk, hogy mekkora eltérést okozna, ha a számításokban a linearizált
alakváltozásoknak megfelelő tenzor-komponensekkel dolgoznánk. Ezek értékét már
korábban kiszámítottuk, most csak felhasználjuk az ellenőrzésnél. Kis alakváltozások esetén
az alábbi feltételezéseket használjuk:
fiz. fiz. fiz.
ε = ε , ε = ε , cosϕ = 2ε
.
X X X Y Y Y c ab X Y
Ebben az esetben például az ab szakasz hossza:
r − r = ε r ⇒ r = r 1+ ε = 1,0 1+ 0,01 = 1,01 ,
ab AB X X AB ab AB X X
22
( ) ( )
vagyis a hossznövekedés ebben az esetben 0,01, ami kb. 2 %-kal tér el a pontos értéktől
(0,010198).
Ha ugyanezeket az ellenőrző lépéseket megismételjük a többi számított mennyiségnél, akkor
a következő eredményeket kapjuk:
r = r 1+ ε = 1,0 1+ 0,04 = 1,04 ⇒ (0,04% − os eltérés)
ac AC Y Y
( ) ( )
1 1
� �
ε X ′ X ′ = ( 0,01 + 0,04) + ( 0,01 − 0,04) cos90 + 0,025sin 90 = 0,05,
2 2
r = r 1+ ε = 2 1+ 0,05 = 1, 4849242 ⇒ (0,1% − os eltérés)
a d AD X X
( ′ ′ ) ( )
fiz. fiz.
�
cos ϕ = 2ε = 2⋅ 0,025 = 0,05 ⇒ ϕ = 87,13402 ⇒ (2,84% − )
c ab X Y c ab os eltérés
c./ A számítás befejezéseként számítsuk ki az AH-tenzor egy elemét és a segítségével
meghatározható oldalhosszat.
A három eltolódásfüggvény az Euler-koordinátákkal kifejezve:
u( x, y, z) = 0,9335111− 0,0093351x + 0,0285768 y,
v( x, y, z) = 1,9051247 + 0,0190512 x + 0,0379120 y,
w( x, y, z)
= 0.
Legyen a keresett AH-alakváltozás például az e y y komponens. A meghatározásához
szükséges képlet:
e
y y
⎡ 2 2 ⎤
∂v 1 ⎛∂u ⎞ ⎛∂v ⎞ ⎛∂w⎞ = − ⎢⎜ ⎥
⎜ ⎟ + ⎜
⎟ + ⎜
⎟
∂y 2
⎢ ⎜ ⎜∂y ⎟ ⎜ ⎜∂y ⎟ ⎜ ∂y
⎟ ⎟⎥
.
⎢⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎣ ⎥⎦
A jobboldal legelső tagja a lineáris alakváltozásoknak megfelelő komponenst ( y y
Behelyettesítve az elmozdulások függvényeit:
∂u ∂v
= 0,02855768, = 0,0379120 ⇒
∂y ∂y
ε ) jelenti.
1
2 2 2
ey y = 0,0379120 − ⎡( 0,0379120) + ( 0,02855768) + 0 ⎤ = 0,0367850, εy
y = 0,0379120.
2 ⎣⎢ ⎦⎥
Ennek az AH-alakváltozásnak a segítségével határozzuk meg például az EF szakasz (eredeti)
hosszát. A számítás lépései hasonlóak az előzőekben alkalmazottakhoz, csak az 1D változás
jellege más, hiszen most
fiz.
l − L
ε = = 1− 1− 2ey
y .
l
A konkrét feladatra alkalmazva 8 :
8 Fontos megjegyeznünk, hogy a „pillanatnyi állapotban” az ef szakasz párhuzamos az y tengellyel,
ezért alkalmazható transzformáció nélkül az AH-tenzor függőleges nyúlási komponense.

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
ε
fiz.
ef E F
y = = 1− 1−2e y y ⇒ r EF = 1−2e y y ⋅ r e f
r e f
r
E F
r − r
= 1−2 ⋅0,0367850 ⋅ 1,03946 = 1,000441.
Ez az érték szintén egyezik a koordinátageometriai úton számítottal. Ha ugyanezt a számítást
a linearizált alakváltozás-komponens felhasználásával határozzuk meg, akkor az elkövetett
hiba nagysága a következő lesz:
r . ef − r
fiz
E F
εy = = εy y ⇒ r EF = ( 1−ε
y y ) ⋅ r e f
r
r
E F
e f
( )
= 1−0,0379120 ⋅ 1,03946 = 1,000000 ⇒
Hosszváltozás ∆ l = 1,039406 − 1= 0,039406,
A pontos hosszváltozás : 1,039406 − 1,000441 = 0,0389649,
A hiba ≈ 1,13%.
6.2. Adott egy (kis alakváltozásokat jellemző) alakváltozás-tenzor. Határozzuk meg a
főnyúlásokat, a főnyíró feszültségeket és az oktaéderes alakváltozásokat!
⎡−0,001 ⎢
Az alakváltozás-tenzor: ε = ⎢ 0
⎢
⎣ 0
Az invariánsok:
0
−0,001
0,000785
0 ⎤
⎥
0,000785⎥
.
⎥
0,002 ⎥
⎦
I ′ =−0,001 − 0,001+ 0,002 = 0,
1
2
3
−9
0 0,001 0,000785 2,62 10 .
23
( )
2 2
−6
I ′ = −0,001⋅ 0,002 −0,000785 −0,001⋅ 0,002 + − 0,001 = −3,62 ⋅10
,
−0,001
0 0
I ′ = − = ⋅
0 0,000785 0,002
A karakterisztikus egyenlet (lásd az 1. alatti lábjegyzetet):
3 −6 −9
ε −3,62 ⋅10 ε−
2,62⋅ 10 = 0 .
Az egyenlet gyökei adják a főnyúlásokat:
ε = 0,00219, ε = − 0,001, ε = − 0,00119 .
1 2 3
Az invariánsok – ellenőrzésre szolgáló – újbóli számítása most a főnyúlásokkal történik:
I ′ =−0,00219 −0,001− 0,00119 = 0,
1
I ′ = ⋅ − + − ⋅ − + − ⋅ = − ⋅
2
−6
(0,00219) ( 0,001) ( 0,001) ( 0,00119) ( 0,00119) (0,00219) 3,62 10 ,
−9
I ′ 3 = (0,00219) ⋅( −0,001) ⋅( − 0,00119) = 2,62 ⋅10
.
Az ellenőrzés igazolta a sajátérték-számítás helyességét.
Határozzuk meg most a legnagyobb nyírási szögtorzulás értékét (Mohr-körös jellemzés,vagy
általános szélsőérték-számítás alapján):
γmax = ε1 − ε3
= 0,00219 − (0,00119) = 0,00338.
A következő feladatrész az oktaéderes alakváltozások számítása. Az oktaéderes
alakváltozások olyan síkokhoz tartozó értékek, melyek normálisai a főirányok által kifeszített

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
térben rendre ⎡
⎢1/ ⎣
3 1/ 3 1/ 3⎤
⎥ értékűek. Az oktaéderes nyúlás ennek megfelelően (az
⎦
ε = ε n n összefüggés segítségével):
n i j i j
1
I ′ 1
εo = ( ε1 + ε2 + ε3)
= = 0 .
3 3
Az ehhez a síkhoz tartozó szögtorzulást térbeli Pithagorász-tétellel számíthatjuk.
γ
Felhasználva a ϑ = tenzori nyírási alakváltozás-jelölést:
2
( ) ( ) 2
1 1 2 2 3 3 1 1 2 2 3 3
2
ϑn =
2 2 2 2 2 2
ε n + ε n + ε n
2 2 2
− ε n + ε n + ε n ,
és behelyettesítve az előbb megadott normálisok komponenseit, a következőt kapjuk a
γ = 2ϑ
kapcsolat figyelembevételével 9 :
okt. okt.
2
2 2 2
1/ 2
γokt. = ⎡( ε1 − ε2) + ( ε2 − ε3) + ( ε3 −ε1
) ⎤
3
⎢⎣ ⎥ .
⎦
Behelyettesítve a numerikus értékeket (mivel az invariánsok már rendelkezésre állnak, az ő
képletüket használjuk, lévén ez a legtömörebb):
2 2 −6
γokt.
= ( 0− 3( −3,62 ⋅ 10 ) ) = 0,00311.
3
Ezeket a változókat főleg a képlékenységtani számításokban használják.
6.3. Határozzuk meg egy adott (kis változásokhoz tartozó) alakváltozás-tenzor deviátoros
részét, valamint a deviátoros invariánsokat!
⎡−0,005 ⎢
Az alakváltozás- tenzor: ε = ⎢−0,004 ⎢
⎣ 0
−0,004
0,001
0
0 ⎤
⎥
0 ⎥ .
⎥
0,001⎥
⎦
A deviátoros rész számításának képlete 10 :
εk
k
ei j = εi j − δi j ,
3
Ennek figyelembevételével:
ahol εk k = ε11 + ε22 + ε33
= − 0,003 .
⎡−0,004 ⎢
ei
j = ⎢−0,004 ⎢
⎣ 0
−0,004
0,002
0
0 ⎤
⎥
0 ⎥ .
⎥
0,002⎥
⎦
Ez a tenzor szintén a képlékenységtani számításokban lesz nagyon fontos mechanikai
jellemző. A deviátoros tenzor első invariánsa a tenzor sajátos felépítése miatt mindig zérus.
A második és harmadik invariáns 11 :
9 Megjegyezzük, hogy ez az érték kifejezhető az alakváltozási invariánsok, illetve az eredeti
alakváltozás-tenzor elemeinek segítségével is:
1/ 2
2 2 2 2
2 2 2 2 2 2
γokt. = ( I ′ 1 − 3I ′ 2)
=
⎡
( εx εy ) ( εy εz ) ( εz εx ) 6(
εx y εy z ε
⎤
⎢ − + − + − + + + z x ) ⎥ .
3 3 ⎣ ⎦
10
Sajnos a deviátoros alakváltozás-tenzor mechanikában használatos szimbóluma megegyezik az
AH-tenzor jelével, ezért mindig ügyelnünk kell tartalmuk pontos magyarázatára.
24

Bojtár-Bagi: Mechanika MSc gyakorlatok anyaga Második hét
1 1 2 2 2 2 2 2
J ′ 2 = ei jei j = ( ex + ey + ez + 2ex y + 2ey z + 2ez
x ) =
2 2
1
2 2 2 2 2 2
=
⎡
( εx εy ) ( εy εz ) ( εz ε
⎤
⎢ − + − + − x) ⎥ + εx y + εy z + εz
x =
6 ⎣ ⎦
1 2 2 2 1 2
= ⎡( ε1 − ε2 ) + ( ε2 − ε3) + ( ε3 − ε1)
⎤ = ( I ′ 1 − I ′ 2)
.
6 ⎣⎢ ⎦⎥
3
ex ex y ex
z
1 1 3 3 3 1 3
J ′ 3 = ei je j kek i = ey x ey ey z = ( e1 + e2 + e3 ) = e1e2e 3 = ( 2I ′ 1 − 9I ′ 1I ′ 2 + 27I
′ 3)
.
3 3 27
e e e
z x z y z
Jelen esetben a numerikus értékek behelyettesítése után:
Felhasznált irodalom:
( ) 2 1
2 2 −5
J ′ 2 = ⎡ 0,006 0 0,006 ⎤ ( 0,004) 2,8 10 ,
6
⎢ − + + + − = ⋅
⎣ ⎥⎦
−0,004 −0,004
0
J ′ = − 0,004 0,002 0
−8
= −4,8⋅10 .
3
0 0 0,002
1./ Technische Noten für Studenten, TU Wien, Institut für Festigkeitslehre, 2002.
2./ Bonet: Nonlinear continuum mechanics for finite elements, Cambridge University Press,
2008.
3./ Kaliszky – Kurutzné –Szilágyi: Szilárdságtan, Tankönyvkiadó, 1998.
4./ Bojtár, I.: Mechanika MSc, BME, 2009.
11 Megjegyezzük, hogy az oktaéderes szögtorzulást is gyakran összekapcsolják a második deviátoros
alakváltozási invariánssal:
γ
2J
′
3
2
okt.
= 2 .
25