2 Statika-Operace s vektory

OPERACE S VEKTORY - 7 -
2.1 Skaláry a vektory. Operace s vektory
Skalár-veličina charakterizovaná číslem (hmota m, objem V, délka l)
Vektor- veličina mající směr i velikost. V ručně psaném textu budeme používat F . Z hlediska
používat zápis a, b, c...
označování v textu budeme pro velikost vektorů a, b,
c
Skalární součin (násobení)- výsledkem je skalár c = a.
b
= a x b x +a y b y +a z b z = a b cos φ, kde φ
je úhel mezi oběma vektory
Vektorový součet c = a + b
- souřadnice vektoru c = ( c
x
,c
y
,c
z
) jsou cy = ay + by
,
cz = az + bz
, cx = ax + bx
.
Vektorový součin c = a xb -souřadnice vektoru c = ( c
x
,c
y
,c
z
) vypočítáme buď rozvojem
determinantu tj.
⎡ i j k ⎤
⎢ ⎥
c = a xb = ⎢ax ay az ⎥ = ( aybz − byaz ) i − ( axbz − bxaz ) j + ( axby − bxay
) k
⎢bx by b ⎥
⎣
z ⎦
nebo pomocí násobení matic
⎡c
⎤ ⎡ 0 −a
x
z ay
⎤ ⎡b
⎤
x
⎢ ⎥ ⎢
⎥ ⎢ ⎥
c = ⎢cy ⎥ = Ab = ⎢ az 0 −ax ⎥ ⎢by
⎥
⎢
c ay
ax
0
⎥
⎢⎣ z ⎥
−
⎦ ⎢⎣
⎥⎦
⎢⎣ bz
⎥⎦
Skalární násobení- výsledkem je skalár c= a .b
=a x b x +a y b y +a z b z =ab cos φ
Poznámka: Dvojího vyjádření pro skalární součin můžeme použít pro určení úhlu mezi
vektory
2.2 Vyjádření sil v kartézské soustavě
Předpokládejme, že na těleso působí v bodě A osamocená síla. Taková osamocená síla je pak
v prostoru určena
a) bodem A , který nazýváme působištěm osamělé síly, působiště je určeno souřadnicemi
x A , y A , z A .
b) vlastní silou F , která působí v působišti A
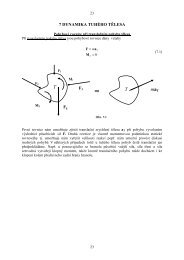
Pro analytický popis sil používáme ve statice kartézskou soustavu souřadnic, která
vytváří pravoúhlý, pravotočivý souřadnicový systém určený trojicí vzájemně na sebe kolmých
jednotkových vektorů báze i , j ,k souřadnicových os x,y,z. Poloha bodu A (viz obr.3.6) je
určena polohovým vektorem rA xAi
y
A
j zA
k
= + + o velikosti
2 2 2
rA = xA + yA + zA
.
Zapisujeme r
A = ( x
A, y
A,z A
) . Směr vektoru síly r
A
je určen jednotkovým vektorem
erA
= cosα i
+ cos β j + cosγ k
kde α , β , γ jsou směrové úhly vektoru r A
. Směrové
úhly odečítáme vždy od kladného směru příslušné osy směrem k vektoru v nejkratším směru
tj. α , β , γ ∈< 0,π >
. Hodnoty směrových úhlů určujících daný směr zpravidla určíme

OPERACE S VEKTORY - 8 -
pomocí jejich kosinů. Pro vektor e
r
platí e = ( )
A
r A
cos α ,cos β ,cosγ , kde
xA yA zA
2 2 2
cos α = , cos β = , cos γ
= . Je zřejmé, že platí cos α + cos β + cos γ =
1. Pro
rA rA rA
zadání směru vektoru tedy stačí znát hodnoty dvou směrových úhlů a interval úhlu třetího,
π
např. α, β,
γ ≤ . Mohou být také zadány 2 směrové kosiny a znaménko kosinu třetího např.
2
cos α,cos β , sign cosγ .
( )
Podobně vektor síly F s působištěm A v soustavě O xyz určíme tak, že do působiště síly
Obr. 2.1
umístíme počátek lokální souřadné soustavy se stejným směrem souřadných os jako má
globální souřadná soustava O xyz . Směrové kosiny pro libovolný směr jsou v obou souřadných
soustavách stejné. Proto zjistíme-li směrové αF , β
F
, γ
F
v lokálním systému, můžeme pak i
pro globální souřadný systém psát F = Fxi + F
y
j + Fzk
. Velikost síly
T 2 2 2
F = F.
F = F + F + F . Velikost síly je přitom nezávislá na volbě vztažného
x y z
souřadného systému tj. říkáme že je to invariant.
Vektorově sílu zapisujeme F = ( F
x
,F
y
,F
z
) = ( F cos αF ,F cos βF ,F cos γ
F
) . Skaláry
F
x
,F
y
,F
z
jsou souřadnice síly, vektory F x = Fx i ,F y = F
y
j ,F
z = Fz
k
jsou složky síly. Přímka
n F je nositelka síly, pro její body platí r = r A
+ λe
. Sílu tedy můžeme
F
zapsat F = F δ
F
eF = Fn en
, kde F
n
je souřadnice vzhledem k nositelce (může to být číslo
kladné i záporné). Toto zadání síly se často vyjadřuje tak, že osamocená síla je určena
působištěm r A
, velikostí F , směrem e n
a orientací (smyslem) δ
F
.
Jednotkový vektor síly určíme ze vztahu
F ⎛
F F
⎞
x y Fz
eF = = ⎜
i + j + k ⎟
= ( cosαFi + cos βF j +
cos β
Fk
)
F ⎝
F F F
⎠

OPERACE S VEKTORY - 9 -
Nositelka síly bývá často zadávána jako spojnice 2 bodů A a B. Míří-li přitom F z bodu A
do bodu B . Pak e F
určujeme ze vztahu
⎛
xB − xA yB − yA zB −
zA
⎞
2 2 2
eF = ⎜
, , ⎟
, kde AB = ( xB − xA ) + ( yB − yA ) + ( zB −
zA
)
⎝
AB AB AB
⎠
Při znázornění síly v rovině sílu F zadáváme jako orientovanou úsečku vedenou z bodu A,
její velikost je nakreslena ve zvoleném měřítku. Měřítko vyjadřuje kolik jednotek síly
odpovídá při znázornění jednotce délky na výkresu. Je-li obrazem síly F
úsečka l F, pak
lF
měřítko m F je mF
= . Průmět síly F p do směru p (určeném jednotkovým vektorem e p
)
F
který svírá s vektorem síly F
úhel ϕ dostaneme pomocí skalárního násobení tj.
F = F.e = F . e cosϕ
=
F cosϕ . Proto souřadnice síly jsou vlastně průměty vektoru síly
p p p
F do směrů příslušných souřadných os.
Vzhledem k tomu, že síla je veličina vektorového charakteru, pro působení sil platí
pravidla vektorového počtu. Působení dvou sil F1 , F2
můžeme nahradit silou jedinou tj.
výslednicí F
pro kterou platí Fv
= F1 + F2
, velikost
2 2
Fv
= F1 + F1 − 2F1 F1
cosϕ
, kde φ je
úhel mezi oběma silami.
v
Pokud platí
F ' = κ F , kde κ je skalár, pak F ' je rovnoběžná s F .