T . maT T .

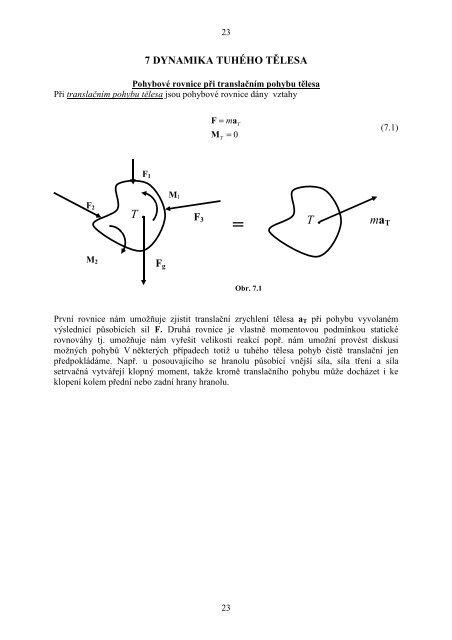
237 DYNAMIKA TUHÉHO TĚLESAPohybové rovnice při translačním pohybu tělesaPři translačním pohybu tělesa jsou pohybové rovnice dány vztahyF = maMTT= 0(7.1)F 1M 1F 2T . F 3.M 2F g=T ..ma TObr. 7.1První rovnice nám umožňuje zjistit translační zrychlení tělesa a T při pohybu vyvolanémvýslednicí působících sil F. Druhá rovnice je vlastně momentovou podmínkou statickérovnováhy tj. umožňuje nám vyřešit velikosti reakcí popř. nám umožní provést diskusimožných pohybů V některých případech totiž u tuhého tělesa pohyb čistě translační jenpředpokládáme. Např. u posouvajícího se hranolu působící vnější síla, síla tření a sílasetrvačná vytvářejí klopný moment, takže kromě translačního pohybu může docházet i keklopení kolem přední nebo zadní hrany hranolu.23

24Příklad 7. 1 Zjistěte zrychlení bedny tvaru krychle o hmotnosti m=50 kg pohybujícího sepůsobením síly P=600 N po horizontální rovině, součinitel smykového tření f=0,2- obr. 7.2.Obr. 7.2Řešení: Vykreslíme schéma uvolněného tělesa s vyznačením zvolené orientace os souřadnéhosystému, směru zrychlení a směru setrvačné síly. Síla P může způsobit jak smýkání krychletak i její překlápění. Pokud by na bednu nepůsobila síla P, bedna by se nepohybovala apůsobiště reakce N C by bylo pod těžištěm. Pokud nemá dojít ke klopení bedny, musí reakceN C mířit do tělesa tj. její působiště musí být v intervalu –0,5 < x < 0,5 m od středu krychle.Jako neznámé jsou N C , x, a a T . Pro třecí sílu platí, že její velikost F =0,2 N C.FaPohybové rovnice ve složkách :x: 600 - 0,2N C = 50a Ty: N C – 50 . 9,81=0z: -0,3.600+x. N C - 0,2 . 0,5N C =0Řešením dostáváme hodnoty: N C =490 N, x=0,467 m, a T =10,0 m/s 2 . Poloha výslednicenormálové složky reakce nám vyšla do tělesa tj. ke klopení krychle tedy nedochází.Poznámka 1: Pokud by poloha reakce N C vyšla mimo hranol byl by to příznak, že dochází kjeho klopení. Přitom pokud je poloha normálové výslednice před přední hranou, tak sepochopitelně jedná o klopení kolem přední hrany, pokud je za zadní hranou, tak se jedná oklopení kolem zadní hrany. Ke klopení kolem zadní hrany by zřejmě mohlo docházet pouzepři poloze nositelky horizontální síly P pod těžištěm.Poznámka 2: Poloha reakční síly N C před bednou je ekvivalentní tomu, že po uvolněníposuvné vazby pomocí reakce umístěné na přední hraně a reakčního momentu mířícího dotělesa by hodnota reakčního momentu vyšla záporná. To by ovšem znamenalo, že reakčnímoment uvolněné posuvné vazby míří od tělesa do podložky, což nelze.24

25V některých případech je vhodné při přímočarém pohybu tělesa použít momentovoupodmínku k jinému vztažnému bodu A než je těžiště T. Pak musíme k momentu od působícíchvnějších sil přičíst i moment od setrvačné síly působící v těžišti. Do schématu uvolněnéhotělesa je proto vhodné zakreslovat do těžiště i směr setrvačné síly, což usnadňuje aplikacimomentové podmínky k obecnému vztažnému bodu. Pro souřadnou soustavu s počátkemO ≡ A pak platí∑ (7.2)x: Fix = maxiy: Fiy = mayi∑ (7.3)z: ∑( MAi ) = ( xi Fyi − yiFxi ) − m( xT ay − yTa ) = 0z ∑ (7.4)iiPříklad 7. 2 Auto dle obrázku má hmotnost m= 2000kg a těžiště v bodě T (obr. 7.3). Určetezrychlení auta, jestliže hnaná zadní kola se neustále protáčí a přední se volně odvalují.Hmotnosti kol m k zanedbejte. Koeficient smykového tření kol je f=0,25.Řešení: Jsou-li hmotnosti kol nulové, pak jsounulové i jejich momenty setrvačnosti a kolanekladou odpor proti roztáčení (). Z tohoovšem vyplývá, že u nepoháněných kol jsouTtečné složky reakcí nulové a ve schématuuvolněného tělesa je nezakreslujeme1 2TA r = Ikα , Ik = mk r = 0 ⇒ TA= 0 .2U hnacích kol však při uvolnění tečné složkyreakcí nenulové jsou a pokud by nedocházelok prokluzu, pak by platiloMhMh− TB r = Ik α = 0 ⇒ TB= ≠ 0 .rVzhledem k prokluzu však platíTB = FB = NBf .aPro vztažný bod T pohybové rovnice:x: 0,25N B =-2000a Ty: N A +N B -2000.9,81=0z: 1,25N A +0,25.0,3N B – 0,75N B =0Neznámé jsou N A, , N B , , a T.TPo dosazení dostáváme numerické hodnoty:a T =1,59m/s 2 , N A =6,88kN, N B =1,7kNPoznámka 1:Pokud momentovou podmínkuzvolíme vzhledem k bodu A, pak v ní nebudeneznámá N A a řešení se zjednoduší, protožepro nalezení a T postačuje systém 2 rovnic:Obr. 7. 3x: 0,25N B =2000a Tz: 2, 0N B− 1, 25. 2000. 9, 81 = 0, 3. 2000aTPoznámka 2: Pokud by hodnota N A vyšla záporná, akcelerace vozidla by byla taková, žedochází ke zvedání předních kol. Poznámka 3: Při smýkání hnacích kol hodnota zrychlenívozidla nezávisí na hodnotě hnacího momentu!25

27Dom. Cv.27

28Pohybové rovnice při rotačním pohybu tělesaPro rovinný případ rotačního pohybu jsou pohybové rovnice ve vektorovém tvaru dányvztahyF = ma (7.5)TMo= Ioα (7.6)Ztotožníme-li osu rotace s osou z tj. o ≡ z , pak ve složkách tyto vektorové rovnice mají tvar2 2∑ Fix = −my α T− mx ω T, ∑ Fiy = −mx α T− my ω T, ∑ Miz= I α z(7.81a)Poznámka: V dynamice pro rovinný případ musí mít těleso rovinu symetrie kolmou na osurotace a zatížení vnějšími silami musí být kolem této roviny také symetrické-např. rotujícídisk poháněný momentem kolmým na rovinu diskuVeličina I oIo2= ∫ dm(7.7)( m)ρje moment setrvačnosti tělesa vzhledem k stálé ose rotace o a ρ je kolmá vzdálenost elementudm od osy rotace.Při rotačním pohybu tělesa je kinetická energie tělesa dána vztahemE1I ω22kr=o(7.8)Platí Steinerova věta, která umožňuje výpočet momentu setrvačnosti tělesa I o vzhledemk libovolné ose o, jestliže známe moment setrvačnosti tělesa I T vzhledem k ose rovnoběžnéjdoucí těžištěm a kolmou vzdálenost e obou os:I I me2o=T+ , (7.9)kde e je kolmá vzdálenost obou os.Součásti strojů jsou zpravidla tvořeny jednoduchými geometrickými tělesy. Vzhledemk aditivnosti integrálu celkový osový moment setrvačnosti složeného tělesa můžeme určit jakoalgebraický součet momentů setrvačnosti jejich vhodně zvolených částí (samozřejměuvažovaných vzhledem k téže ose nebo rovině. Např. pro těleso na obr. 7.10 počítámeI = I + I + I + I0 01 02 03 04Obr. 7. 1028

29Příklad 7. 3 Kyvadlo na obr. 7.11 se skládá ze dvou tyčí, každá z nich váží 4,5kg. Vypočtětemoment setrvačnosti k ose jdoucí bodem O a k ose procházející těžištěm T, je-li l=0,3m.Řešení:Nejprve vypočítáme moment setrvačnosti první tyče OA :I1o( ) 2 22l4,5⋅0,6m⋅= = =3 320,54 kg.m .Moment setrvačnosti tyče BC pomocí Steinerovy věty( l)2 22 ⋅2 2m⋅2 4,5 0,6Obr. 7. 11 I2o= + m⋅ ( 2l)= + 4,5⋅ 0,6 = 1,76 kg.m .12 12Moment setrvačnosti celého tělesa k O je podle (5.25):2Io = I1 o+ I2o= 0,54 + 1,76=2,3 kg.mVypočítáme polohu těžiště:y1 ⋅ m1 + y2 ⋅ m m⋅ 2( y1 + y2 ) ( y1 + y2) 0, 3 + 0,6y = = = = = 0, 45m.m + m 2⋅m2 21 2Moment setrvačnosti celého tělesa k ose procházející těžištěm pak určíme pomocí Steinerovyvěty:2I = I − m⋅ y = 2, 3− 4, 5⋅ 0, 45 = 1,4 kg.mTo2 229

30Statické vyvažováníStaticky vyvažujeme krátké rotační součásti (setrvačníky, řemenice), u kterých kvůlinepřesnosti výroby osa otáčení neprochází. Statickou nevyváženost odstraníme tak, že naprotilehlé straně od těžiště přidáme hmotu, nebo na stejné straně od osy rotace hmotu uberemetak, aby se těžiště dostalo do osy rotace. Statickou nevyváženost odstraníme tak, že naprotilehlé straně od těžiště přidáme hmotu, nebo na stejné straně od osy rotace hmotu uberemetak, aby se těžiště dostalo do osy rotace. Tuto hmotu je nutné přidat v takové vzdálenosti odosy rotace, aby platila rovnováha odstředivých sileω = ω ⇒ = (7.10)2 2me mpr mpm rkde m je hmotnost rotoru, e je vzdálenost těžiště od osy rotace, m p je přídavná nebo odebranáhmotnost, r vzdálenost umístění hmotnosti m p od osy otáčení. Statické vyvážení rotoru lzeprovést jedinou hmotou.Dynamické vyvažováníI když je rotující těleso staticky vyváženo (tj. jeho těžiště leží na ose rotace), může rotujícítěleso způsobovat namáhání ložisek. Např. rotující deska skládající se ze dvou stejnýchtrojúhelníků má těžiště desky sice leží na ose, zároveň je však zřejmé, že za rotace vznikajídvě odstředivé síly vytvářející silovou dvojici, která namáhá ložiska. Poněvadž dvojici sil jemožné uvést do rovnováhy zase jen dvojicí, znamená to, že dynamické vyvážení je v tomtopřípadě možné jen dvěma vývažky ležícími v různých rovinách. Volba těchto rovin zpravidlabývá podmíněna konstrukčními možnostmi umístění vývažků.30

3131

32Příklad 7. 8 Setrvačník S o momentu setrvačnosti I o se rozbíhá z klidu působením třecí spojkymající stálou rychlost ω k . Spojka je přitlačována k setrvačníku stálou silou P, součinitelsmykového tření je f. Určete dobu t k , za kterou se setrvačník rozběhne na úhlovou rychlost ω khnacího hřídele, celkové pootočení setrvačníku φ k (Obr. 7.15).Řešení: Tlak na spojce je p =πP2 2( r2 − r1)Infinitezimální normálová tlaková síla na spojku působící na mezikruží dS = 2πrdrje dF = p dS = p2πrdrpInfinitezimální moment třecích sil2dMo= rdFp= 2πpfr drCelkový moment třecích sil spojky je tedy rovenM( )2 2( r2 − r1)( )π π Pf r − r 2Pf r + r r + rπr3 3 2 212 2 2 1 2 2 1 1o= ∫ 2 r fpdr = =3 3r( r )12+ r1Vlastní pohybová rovnice pro rotační pohyb roztáčeného setrvačníku je2 22Pf ( r2 + r2 r1 + r1)Mo= = Ioα3 r + r( )2 1Jedná se tedy o pohyb s konstantním úhlovým zrychlením. Aplikací vztahuintegrací tedy dostáváme pro dobu roztočení setrvačníku hodnotuIoω k3( r2 + r1)tk=2 22P r + r r + r f( 2 2 1 1 )Celkové pootočení setrvačníku ϕkpak získáme integrací vztahuωk ϕk ϕk22Modω = 2α dϕ = dϕI∫ ∫ ∫0 0 0( )oObr. 7. 15( )4Pf r + r r + r 3 I r + rω ϕ ϕ2 2 222 1 2 1 ωko 2 1k=k⇒k=Io3( r2 + r1 )4 f P r2 + r1 r2 + r12 2( )2( ω )dα = :2dϕdωα = adt32

33Homogenní tyč délky L, otočná kolem osy kolmé na tyč a jdoucí jejím koncem, padá ze svislépolohy na vodorovnou rovinu (obr. 3.9). Vyjádřete závislost rychlosti koncového bodu tyčena úhlu odklonu od svislého směru.[ v = 3gL( 1−cosϕ )]33

34Pohybové rovnice při obecném rovinném pohybuF = maMTT= I αT(7.11)Dynamiku obecného rovinného pohybu tělesa můžeme řešit jako dynamiku translačníhopohybu hmoty soustředěné v těžišti (na kterou působí výslednice vnějších sil) a rotačníhopohybu tělesa kolem těžiště (pod působením výsledného momentu vnějších sil).Poznámka: V případě, že translační a rotační složka pohybu tělesa jsou vázány (např. přiodvalování kotouče), pak je nutné do schématu uvolněného tělesa zakreslit orientacetranslačního a úhlového zrychlení tak, aby si navzájem odpovídaly -viz obr. 7.20.V případě přímočarého pohybu těžiště pro složkový zápis rovnic (7.11) budemepoužívat souřadnice kartézské tj.Fx = maTx; Fy = maTy;MT = ITα(7.12)Jestliže dráha pohybu těžiště bude křivočará, pak pro zápis složkových pohybových rovnicpoužijeme přirozené souřadnice okamžité tečny a normály dráhy těžištěFt = maTt;Fn = maTn;MT = ITα,Pro kinetickou energii tělesa konajícího obecný rovinný pohyb vztah1 2 1 2Ek = mvT + ITω(7.13)2 2Slovy: Kinetická energie tělesa, konajícího obecný rovinný pohyb je dána součtem kinetickéenergie hmotnosti soustředěné v těžišti a kinetické energie rotačního pohybu kolem těžiště.34

35Příklad 7. 6 Určete maximální úhel sklonu βmax nakloněné roviny, při kterém ještěnedochází ke smýkání plného válce o poloměru r (obr. 7.20). Z hodnoty tohoto úhlu určetesoučinitel smykového tření f mezi válcem a nakloněnou rovinou.Schéma uvolněného tělesa:yS ≡ TPαa TF t F nŘešení: Nejprve zjistíme hodnotu zrychlení středu válce při za předpokladu, že dochází k jehoodvalování při obecném sklonu sklon nakloněné roviny. Zvolíme-li jako vztažný bod těžiště,pak pro zvolený souřadný systém pohybové rovnice jsou vektorové pohybové rovniceF + F + F = mag n t TMT= ITαVe složkách:x: ... mg sin β − Ft = maTy:... F − mg cos β = 0nz:... − Ft r = − ITαPro moment setrvačnosti válce k ose totožné s jeho geometrickou osou použijeme známý1 2vztah IT= mr2Má-li docházet k odvalování válce, musí být dále splněna podmínka valení aT= αr.V rovnicích máme 4 neznámé aT,Fn,Ft,α . Pro hodnotu zrychlení středu válce dostáváme2výsledek aT= g sin β ,3Při maximálním úhlu sklonu β = β kdy ještě dochází k odvalování je tečná složkamaxreakce Ftrovna třecí síle tj. Ft = Fn f = mg cos βmax. Pak můžeme kombinací podmínky valení2a vztahu pro zrychlení středu kotouče aT= g sin βmaxurčit z první rovnice hodnotu31součinitele smykového tření f = tgβmax.3V případě, že bychom jako vztažný bod použili pól rychlosti P, pak pohybové rovniceve složkách by měly tvar:x: ... mg sin β − Ft = maTy:... F − mg cos β = 0nObr. 7. 20z:... − mg sin βr = − IPα2 3 2Hodnotu I P určíme za pomoci Steinerovy věty tj. IP= IT+ mr = mr .2Výpočet neznámých F t , a T, , α je při použití druhého systému rovnic je jednodušší.xNF g35

36U některých úloh je někdy účelné kombinovat pohybové rovnice pro jednotlivé složkypohybu tělesa se zákony zachování energie nebo hybnosti nebo momentu hybnosti:Příklad 7.7. Koule je vržena počáteční rychlostí v T0 téměř tečně na podložku, koeficientsmykového tření je f. Určete čas ∆ t po který se koule smýká, na jaké dráze ∆xse smýká ajaká je její konečná rychlost v Tk po ukončení smýkání.Řešení: Hodnota třecí síly je při smýkání konstantní, můžeme tedy použít vztah pro impulsmomentu I o a zjistit dobu trvání smýkání:∆tI = ∫ M dt = M ∆t = r F ∆t = r m f g ∆t = B − B ,o o o tř o2 o10kde Bo2 ,Bo1jsou momenty hybnosti na začátku a na konci smýkání. Pro moment hybnosti2 2odvalující se koule platí vztah Bo= ITω= mr ω . Na začátku smýkání se koule5neodvalovala tj. Bo1 = 0 . Na konci smýkání už začíná odvalování, tedy můžeme použítpodmínku valení vTk= ωk( v Tkje rychlost středu koule a ωkje úhlová rychlost rotační složkypohybu koule na konci smýkání). Změna momentu hybnosti je tedy rovna2Bo 2− Bo 1= mrvTk5Dosazením do 1. rovnice pak dostáváme vztah pro dobu trvání smýkání tj.2v ∆ t = Tk5 fgVyužitím pohybové rovnice pro translační složku pohybu dostaneme zrychlení a T středukoule při smýkáníFtřFtř = maT ⇒ aT= = fgmZ hodnoty tohoto zrychlení pak můžeme pomocí vztahu pro rovnoměrně zpožděný pohybzjistit rychlost vTkpři ukončení smýkání5vTk = vT 0− aT∆t = vT07Ze zákona zachování energie dostaneme vztah pro dráhu ∆ x na které třecí síla působila21 2 1 2 1 2 12 v0mvTk + Iωk + Ftř∆x = mv0⇒ ∆x=2 2 2 49 fg36

3737

38Dynamika sférického pohybu tělesaSférický pohyb koná těleso, jehož jeden bod je nepohyblivý.Těžký (nedochází ke změně velikosti hodnoty vlastní úhlové frekvence) symetrický setrvačník- jedná se o těleso otáčející se konstantní úhlovou rychlostí ϕɺ kolem své geometrické osy,konstantní precesní úhlovou rychlostí ψɺ a konstantní hodnotu nutačního úhlu ϑ . Jedná setedy o 2 současné různoběžné rotace, reakcí na takový pohyb je vznik setrvačnéhoπgyroskopického momentu M G. Pro úhel ϑ = přesně nebo pro vysoké hodnoty úhlové2rychlosti vlastní rotace tj. ɺϕ ≫ ψɺpřibližně můžeme pro gyroskopický moment psát vztahM( ψ )G= I0xkde I o je moment setrvačnosti vzhledem ke geometrické ose.Nebo takékde je Résalovo zrychleníαR=ϕɺ x ψɺ .Gϕɺ ɺ , (7.121a)M = −I α (7.121b)Gyroskopický moment je kolmý na vektory úhlových rychlostí rotace a precese a jeho smysl jetakový, že se snaží ztotožnit nejkratší cestou osu vlastní rotace s osou precese.Kompenzací vznikajícího gyroskopického momentu můžeme stabilizovat pohyb těles. Např.při horizontálním uložení těžkého setrvačníku kolmo na podélnou osu lodě při kývání loděpodél její osy vzniká gyroskopický moment, který se „snaží“ loď otočit kolem svislé osy.Tento pohyb je však kompenzován velkou hodnotou odporového momentu vody působícímna boky lodě při jejím pohybu v příčném směru a je tím zabráněno vznikající precesnírychlosti ψɺ kývání lodi.0R38

3939