1 Statika-Operace s vektory. Síla a moment síly-cvičení

1 VEKTOROVÝ POČET. SÍLA A MOMENT SÍLY Vektorový součet c = a + b. Souřadnice výsledného vektoru c = ( cx,cy,cz)cy = ay + by, cz = az + bz, cx = ax + bx.jsouSkalární součin (násobení)- výsledkem je skalár c = . = a x b x +a y b y +a z b z = a b cos φ, kde φje úhel mezi oběma vektoryPoznámka: Dvojího vyjádření pro skalární součin můžeme použít pro určení úhlu mezivektorya b Vektorový součin c = a xb -souřadnice vektoru c = ( cx,cy,cz) vypočítáme buď rozvojemdeterminantu tj. ⎡ i j k ⎤ ⎢ ⎥ c = a xb = ⎢ax ay az ⎥ = ( aybz − byaz ) i − ( axbz − bxaz ) j + ( axby − bxay) k⎢bx by b ⎥⎣z ⎦Průvodič bodu A - vektor r Aspojující počátek O souřadné soustavy s bodem APlatí: r Ax Ai y Aj z Ak = + + , velikost2 2 2rA = xA + yA + zA. Zapisujeme r A = ( x A, y A,z A) .Vyjádření sil v kartézské soustavěVektorově sílu zapisujeme F = ( Fx,Fy,Fz) = ( F cos αF ,F cos βF ,F cos γF) . Fx,Fy,Fzjsousouřadnice síly, úhly αF , βF, γFjsou tzv. směrové úhly, které vektor síly svírá se směremsouřadných os. Velikost sílyF = F + F + F .2 2 2x y zSílu můžeme také vyjádřit pomocí jednotkového směrovéhovektoru e = F(cos α F,cos β F,cos γ F) . Platí F = F e .FLeží-li F na spojnici z bodu A do bodu B , pak e Furčujeme ze vztahu ⎛xB − xA yB − yA zB −zA⎞2 2 2eF = ⎜, , ⎟, kde AB = ( xB − xA ) + ( yB − yA ) + ( zB −zA)⎝AB AB AB⎠1

Obr. 2.12

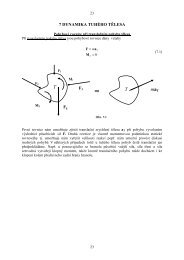
Př. 1 Zapište síly F 1 , F 2 a F 3 ve složkovém tvaru. Najděte výslednou sílu působící v oku A. Najděte výslednýmoment vzhledem k bodu B o souřadnicích [3cm,2cm]AAAABFFF123Řešení := 850⋅(cos36,87i− sin36,87 j)= 680i− 510 j [ N]= 625⋅(−sin30i− cos30 j)= −312,5i− 541,3 j [ N]= 750⋅(−cos45i+ sin 45 j)= −530,3i+ 530,3 j [ N] FV= −162,8i − 521,0 j[ N ] M = ( − 162,8.3+ 521,0 .2) k = 533,6 k[ N. m]B3

Př. 3Úhel θ má být v intervalu (0,90 0 )Pro velikost výslednice platíFV= 900+ 1600+1200cos( θ )dFV=−1200sin( θ )dθ 2 2500+1200cos( θ )= → =0 podmínka proextrém jesiceθ0, tentoextrém je však maximum (2. derivace je pro θ =0 záporná!). OddFVhodnoty θ=0 závislost FV( Θ ) monotoně klesá (derivace je záporná),takže nejmenší hodnota je pro horní okraj zadaného intervalu tj. θ=90 0dΘ4

Pokud F∑A+ F má ležet na x,pak musí platitBF O F F θ F0ix= :Acos30 +Bcos −R= 0∑F O F F θ F0Biy= :Asin 30 −Bsin = 0 ⇒A= .0Dosazením do horní rovnice získáme funkci FdFBPodmínka proextrém = 0 ⇒ θ = 60d θ0F sinθsin 30B= F ( θ ) =Bcosθ+FR3sinθTento extrém je minimum (hodnota 2. derivace je pro θ =60 0 kladná)Poznámka: 1. rovnice zajišťuje posun klády– výslednice sil v lanech je zřejmě rovna smykovésíle působící na kládu2. rovnice zajišťuje to, že ve směru y je rovnováha tj. kláda se bude pohybovat ve směru x5

Moment sílyM OMoment síly k počátku O je dán vektorovým součinem r A(ramene síly)a vektoru síly F i j k yAzA xAz xA AyA MO= xA yAzA = i − j + k = ( yAFz − zAFy ) i + ( zAFx − xAFz ) j + ( xAFy − yAFx) kFy Fz F FxFzxFyF F Fx y z Moment síly MB= rBAx F k libovolnému bodu B je určen vztahem MB= rBAx Fje vektor jdoucí z bodu B do působiště síly A, kde r BAVelikost momentu síly M = r x F .e ,( )p BA pMpvzhledem ose p definujeme pomocí vztahu:kde B je libovolný bod na ose p, A je působiště síly F . Jedná se o smíšený součin, pro kterýplatí( x − x ) ( y − y ) ( z −z )A B A B A BM = F F F=p x y zcosα cos β cosγp p p( ) ( ) ( )( ) ( ) ( )= F z − z cos β + F x − x x cosγ + F y − y cosα−x A B p y A B A p z A B p− F y − y cos γ − F z − z cosα − F x −x cos βx A B p y A B p z A B p7

Vektor momentu síly M = M ep p pM pvzhledem k orientované přímce p a je rovenMoment silové dvojice je výsledný moment od dvou sil stejně velkých ale opačněorientovaných sil, jeho velikost je rovna M = F r , kde r je kolmá vzdálenost nositelek. Směrtohoto vektoru určíme podle pravidla pravé ruky, je to vektor volný v prostoru.10

Věty o silách a momentechZ axiomů mechaniky a z pravidel vektorového počtu vyplývají o silách a momentech důležitévěty:V1 (Věta o posunutí síly po nositelce)- Síla F je staticky ekvivalentní s každou silou stejnévelikosti a smyslu ležící na nositelce n F . Jinými slovy- účinek síly na těleso se nezměníjestliže se působiště síly libovolně posune po nositelce. Síla je tedy vektor volný na přímce.V2 (věta o 2 silách)- dvě síly jsou v rovnováze tehdy a jen tehdy, jestliže leží na společnénositelce, jsou stejně velké a jsou opačně orientované. Jinými slovy - síla F je v rovnovázes každou silou stejné velikosti a opačného smyslu, obě síly však musí ležet na společnénositelce. Tyto 2 síly vytváří soustavu nulového vektoru.V3 (věta o 3 silách)- 3 síly jsou v rovnováze tehdy a jen tehdy jestliže se jejich nositelkyprotínají v jednom bodě, síly leží v jedné rovině (jsou komplanární) a součet dvou sil je stejněvelký, ale opačně orientovaný než síla třetíV4 - K tělesu je možné přidat nebo ubrat rovnovážnou silovou soustavu aniž by se změniljeho pohybový stav.V5 - Každou sílu můžeme jednoznačně rozložit v prostoru do 3 nekomplanárních směrů(směry přitom nemusí být na sebe kolmé). V rovině můžeme každou sílu rozložit do 2různých směrůV6 (Varignonova věta 1) - Moment síly F vzhledem k libovolnému bodu je vektorovýmsoučtem momentů od jejích složek k témuž bodu. V9 –Pro počátek O kartézské soustavy platí ( MO ) = Mx,( MO ) = My,( MO ) = Mz . Jinýmix y zslovy- moment síly k jednotlivým osám je roven průmětu momentu síly M Ovzhledemk počátku do směru jednotlivých osV10- Moment síly M p vzhledem k přímce p je nulový jestliže nositelka F přímku protíná neboje s ní rovnoběžnáV11- Moment silové dvojice je vektor volný v prostoru11

Příklad 4 Na těleso působí síly podle obrázku.Dáno:Výslednicí je moment . Síly působící v bodech A a C tvoří silovou dvojici.Velikost silové dvojice je dána vztahemPodobně pro silové dvojice tvořené silamiMomenty od silových dvojic jsou vektory volné v prostoru. V daném případě jsou všechnymomenty rovnoběžné, můžeme je tedy sčítat algebraicky s ohledem na znaménko. Výslednýmoment je:12

Př. 5 Moment síly – Užití Varignonovy věty Určete momenty sil k bodu A.Obr.1Dáno: ; ; ; ; ; ;Určit:Řešení:Pro výpočet momentů sil použijeme Varignonovu větu.Rozložíme síly do složek x, y.Moment síly je dán vektorovým součtem momentů složek síly k témuž bodu. Kladný smyslmomentu uvažujte proti smyslu pohybu hodinových ručiček.14