3 Statika-Síla a Moment síly

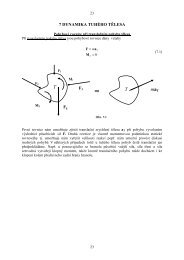
SÍLA A MOMENT SÍLY - 10 -3. Silové působení na hmotné objekty3.1 Síla a její posuvné účinkyV této kapitole si popíšeme vlastnosti silových účinků působících na konstrukce a reálnémechanické soustavy. Zavedeme kvantitativní popis síly jako vektorové veličinycharakterizující míru interakce (vzájemného působení) mezi tělesy.Účinek síly na hmotný objekt přitom může být statický nebo dynamický. Přidynamickém působení se mění pohybový stav studovaného objektu tj. dochází ke změněrychlosti jednotlivých bodů tělesa. Jsou li vazby působící na těleso takového charakteru, žetěleso může konat jen pohyb posuvný (trajektorie všech bodů tělesa jsou stejné, navzájemposunuté křivky), pak rychlosti všech bodů tělesa jsou stejné. Při silovém působení je pakzměna rychlosti všech bodů orientována ve směru působící síly a vztah mezi působící silou avyvolanou změnou pohybového stavu je vyjádřen pomocí 2. Newtonova zákonad ( mv )F = , (3.1)dtkde F je výslednice všech sil působících na těleso.Při statickém účinku sil na těleso podrobené vazbám umožňujícím jen posuvný pohybnedochází ke změně rychlosti, protože všechny síly působící na objekt jsou v rovnováze ajejich účinek se vzájemně vyruší. Platí tedy vztahF = 0(3.2)3.2 Rozdělení silPojem síly vznikl generalizací a abstrakcí subjektivního lidského pocitu tahu nebotlaku. Příkladem může být působení lana na konzolu Jeho abstrakce je reprezentovanávektorem (viz obr.3.1), který leží na přímce p (nositelce síly) a prochází bodem tělesa(působištěm). Vzájemné působení těles přitom nemusí být uskutečňováno přímým kontaktemtěles, nýbrž i působením na dálku tj. silovým polem. (např. polem gravitačním).Jak je z názoru popř. z obr. 3.1 zřejmé, pro určení síly jako fyzikální veličiny je nutné zadatmísto jejího působení (působiště), směr, smysl působení (orientaci) na určité přímce(nositelce) a konečně velikost síly tj. míru intenzity jejího působení. Síla má tedy charaktervektoru vázaného na bod a její účinky na těleso jsou jednoznačně popsány pomocí působiště,velikosti, směru působení a orientace.Obr.3.1

SÍLA A MOMENT SÍLY - 11 -Graficky sílu znázorňujeme pomocí orientované úsečky F , počátek této úsečky (v případě žese jedná o tahovou sílu) nebo konec této úsečky (v případě že se jedná o tlakovou sílu)umisťujeme do působiště. Měřící jednotkou pro vyjádření velikosti síly je [F]=[kg.m.s -2 ]= [N](Newton). Při znázorňování síly v rovině používáme měřítka tj. délka úsečky vektoru sílyv geometrických jednotkách (např.v cm) je úměrná velikosti síly ve fyzikálních jednotkách(např. v Newtonech), šipka přitom určuje smysl působení síly.Jestliže působiště sil je omezeno na malou plošku, jejíž velikost můžeme oproti plošepovrchu hmotného objektu zanedbat tj. můžeme ji se zanedbatelnou ztrátou přesnostisoustředit do bodu, pak takové síly budeme nazývat soustředěné (bodové, izolované,osamocené) síly. V případě, že působení sil není omezeno na bod, pak budeme hovořit ospojitém silovém působení (např. síly na kontaktu pneumatiky s vozovkou, síly v čepech,gravitační síly působící v prostoru tělesa apod.).3.3 Otáčivé účinky sílyV případě, že vazby působící na těleso jsou takového charakteru, že umožňují pouze pohybrotační (např. ložiska), pak při silovém působení může docházet otáčení tělesem tj. tělesa jsouuváděna do rotačního pohybu (viz obr. 3.7). Při dynamickém silovém působení je pak změnapohybového stavu při rotačním pohybu určena vztahem d ( ω )Mo= Io(3.3)dtkde M oje výsledný moment od všech působících sil na těleso vzhledem k ose rotace o, I o jemoment setrvačnosti tělesa vzhledem k ose rotace o a ω je úhlová rychlost rotace.Při statickém působení je výsledný moment všech působících sil nulový a nedocházítedy ke změně hodnoty úhlové rychlosti. Platí tedyM = 0(3.4)o0br. 3.23.3.1 Moment síly k boduPro schopnost síly otáčet tělesem se používá termín moment síly k bodu tělesa.Velikosttočivého účinku přitom závisí jak na velikosti síly F, tak i na velikosti ramene p (viz obr.3.7).

SÍLA A MOMENT SÍLY - 12 -Moment síly k bodu je pak vektor resp. kolem osy procházející kolmo na rovinu vytvořenousilou a polohovým vektorem jejího působiště.Předpokládejme že těleso je uloženo v bodě O, jehož poloha se nemění. Otáčivýúčinek síly F s působištěm v bodě A k bodu O pak vyjadřujeme vektorem MO = rAx F (vizobr. 3.8). Moment síly k bodu je tedy vektor vázaný na bod O (k jinému vztažnému bodu jemoment síly F jiný, proto používáme pro jeho označení vztažný bod O jako index), je kolmýna rovinu vytvořenou vektory r a F a je orientovaný na tu stranu roviny, odkud se jevíA otáčení v kladném smyslu (soustava vektorů r , F,M je pravotočivá). Směr vektoru M určíme pomocí pravidla pravé ruky tak, že prsty ukazují směr otáčení a palec přitom ukazujesmysl orientace vektoru momentu – obr. 3.9. Při rovinných úlohách leží rameno síly i vektorsíly v jedné rovině, kterou použijeme jako nákresnu. Moment síly pak označujeme kladně (+)pokud má tendenci otáčet těleso proti smyslu otáčení hodinových ručiček resp. zápornýmznaménkem (-) pokud má tendenci otáčet tělesem ve smyslu otáčení hodinových ručiček (tatodohoda odpovídá kladné resp. záporné orientaci vzhledem ke kartézské ose z vystupující znákresny).AOOM OObr. 3.3 Obr. 3.4 Poznámka: Pro vektorový součin neplatí komutativní zákon tj. MO≠ F x rA.Jak vyplývá z definice vektorového součinu, velikost M O =r A Fsinϕ =F p=F t r A , kde p=r A sinϕ,F t =Fsinϕ. Jsou-li vektory rA, F určeny souřadnicemi x A , y A , z A , F x,, F y, F z pak moment M Ojevyjádřen ve tvaru známém z vektorového počtu: i j k y AzA xAzxA yAAMO= xA yAzA= i − j + k =FyFz FxFFz xFy(3.5)FxFy Fz= ( y F − z F ) i + ( z F − x F ) j + ( x F − y F ) kA z A y A x A z A y A x

SÍLA A MOMENT SÍLY - 13 -Obr. 3.5 Obr. 3.6Výrazy v závorkách jsou souřadnicemi vektoruM O.Z vlastností vektorového počtu přímo plynou dvě následující věty (tzv. Varignonovy). M = r xF = r x( F + F + F ) = r xF + r xF + r xF )O A A x y z A x A y A zcož můžeme slovy formulovat takto:Moment síly k bodu O je roven vektorovému součtu momentů od jejích složek., (3.6)Tato věta se s výhodou používá při numerických výpočtech hodnot momentů. Např. jestližepočítáme moment síly F k ose z, nepočítáme podle obr. 3.10 neboť neznáme vzdálenost p, alevýhodněji podle obr. 3.11. Obdobně, jestliže v bodě A působí soustava sil F1,.........,F n, pak moment od této soustavymůžeme nahradit momentem od výslednice tj. platí M = r x F = r x F = ( r x F ) =M , (3.7)∑ ∑ ∑O A v A i A i Oicož můžeme formulovat takto: Moment od výslednice soustavy sil se společným působištěmje roven vektorovému součtu momentů od jednotlivých sil.Poznámka : Moment M Oje nulový, jestliže velikost F je nula nebo nositelka n F procházívztažným bodem O.3.3.2 Moment síly k oseMoment síly k bodu je vždy kolmý na rovinu obsahující rameno síly a vektor síly. V praxivšak často potřebujeme znát i otáčivý účinek síly vzhledem k ose rotace p, která není kolmána vektor působící síly. Předpokládejme,že těleso je uloženo v ose p. Pak se toto těleso(obr.3.12) působením síly F s působištěm v A může otáčet kolem osy p. Moment síly k libovolnému bodu B ležícím na p je určen vztahem MB= rBAx F . Z toho je zřejmé, žemoment MBje závislý na poloze vztažného bodu B na ose p tj. otáčivý účinek síly F k ose pnemůže být tedy charakterizován momentem M . Musíme tedy nalézt takovou složku M ,BB

SÍLA A MOMENT SÍLY - 14 -která bude pro všechny body B přímky p stejná. Jak vyplývá z obr. 3.12, násobíme-li MBskalárně jednotkovým vektorem e p, pak dostaneme MB.ep = ( rBA x F ) .ep = ( rA x F ) .ep − ( rOB x F ) .ep =( rA x F ) .ep , neboť ( rOBx F ) .ep= O . Veličina MB.ep je tedy stejná pro všechny body B ležící na přímce p a je to souřadnicevektoru MBvzhledem k ose p. Proto moment síly F působící v bodě A vzhledem k ose pdefinujeme pomocí vztahu: Mp = Mp.ep, kde Mp = MB.ep = ( rBA x F ) .ep, B ∈p(3.8)Moment síly F je tedy vektor vázaný k přímce p a je roven průmětu momentu sílyF vzhledem k libovolnému bodu B ∈ p do osy p. Vyjádříme-li jednotlivé vektory rA, F , epsouřadnicemi, pak z vektorového počtu jeznámo, že smíšený součin a pro velikost momentu M p můžeme použít vztahx y zA A AM = F F F=p x y zcosα cos β cosγp p p= F z cos β + F x cosγ + F y cosα − F y cosγ − F z cosα −F x cos βx A p y A p z A p x A p y A p z A p(3.9)Počátek O kartézské soustavy souřadnic je bodem osy x. Podle předcházejícího tedy platí, žex-ová složka momentu M Oxje rovna momentu Mxk ose x. Podobně O je bodem osy y a osyz tj. platí MOx = Mx,MOy = My,MOz =Mz(3.10)Moment síly F k počátku O je tedy roven součtu (vektorovému) momentů téže síly F ketřem osám kartézského souřadného systému tj. můžeme psát M = M + M +M (3.11)Uvažujme nyní dva zvláštní případy:O x y za) Síla F je rovnoběžná s osou p, takže potom platí Mp = ( rBA x F ) .ep = ( F x ep ) .rBA=0b) Nositelka síly F protíná osu p. Pak položíme-li vztažný bod B do společnéhoprůsečíku, je r BArovnoběžná s F tj. rBAx F = 0 a tedy opět M p =0.Platí tedy: Moment síly F k ose p je nulový když nositelka síly F je rovnoběžná s osou pnebo když osu p protíná.

SÍLA A MOMENT SÍLY - 15 -r BAr OBxObr. 3.73.3. 3 Moment silové dvojiceZvláštním případem silové soustavy je soustava dvou sil stejně velkých ale opačněorientovaných sil. Takové soustavě říkáme silová dvojice (obr.3.13) Silová dvojice mázvláštní vlastnosti, které využíváme v každodenním životě- např. otvírání kohoutku, otáčenívolantu apod. Uvažujme silovou soustavu tvořenou dvěma silami F1a F2, které jsou stejně velké tj. F 1 =F 2 = F a opačně orientované tj. e = −e . Pak platí:F1 F2F 1 2( ) 0 V= F + F = F + − F = Pro výsledný moment sil F1 , F2k bodu O platí M = M1 + M2= r1 x F + r2 x ( − F)= r x FO O OJeho velikost M=F 1 r sinϕ=konstZ těchto rovnic vyplývá, že při působení dvou stejně velkých, opačně orientovaných sil jeF V= Oa M0= MA= M = konst Obr. 3.8

SÍLA A MOMENT SÍLY - 16 -Silová dvojice má tedy vzhledem k libovolnému bodu A stejný rotační účinek a nulovýúčinek posuvný. Vektor momentu silové dvojice je tedy vektor volný v prostoru, jeho velikostje rovna součinu jedné ze sil a kolmé vzdálenosti obou nositelek, jeho orientace je kolmá narovinu určenou nositelkami obou sil a jeho smysl je určen pravidlem pravé ruky (viz obr.3.14).Obr. 3.9Obr. 3.10 Obr. 3.11Obr. 3.12 Obr. 3.13

SÍLA A MOMENT SÍLY - 17 -Vzhledem k tomu, že vektor momentu silové dvojice je vektor volný v prostoru, dvojicí lze1) libovolně posouvat nebo otáčet v rovině (3.15)2) libovolně posouvat do rovin navzájem rovnoběžných s rovinou dvojice sil (obr.3.16)3) vykonat redukci dvojice (tj. nahradit jí jinou dvojicí) tak, aby platilo M=F 1 p=F 1´p´(viz obr.3.17).Jestliže na těleso působí několik silových dvojic v navzájem rovnoběžných rovinách, můžemeje myšleně přemístit do bodu jedné roviny a algebraicky sčítat s ohledem na znaménka tj. M = ∑ M i. Jestliže silové dvojice působí v různoběžných rovinách, po přemístění do libovolného bodu prostoru je můžeme sčítat vektorově. Výsledný moment je M = M1 + M2 ,přitom silová dvojice tohoto momentu leží v rovině kolmé na M (obr. 3.18).Působí-li na těleso n silových dvojic, pak všechny tyto dvojice můžeme nahradit v libovolnémmístě tělesa jejich momenty M , M ,…1 2M n. Protože jde o vektory procházející jednímbodem, určíme výsledný moment jejich vektorovým součtem tj.MV= ∑ MiPoznámka k označování:M B- moment síly F k bodu BM p- moment síly F k ose pM -moment silové dvojice ( F ,- F )Při znázorňování silové dvojice v její rovině, tj. v rovině určené rovnoběžnými nositelkami,budeme užívat tuto symboliku (viz obr. 3.14a a 3.14b):⇔⇔⇔⇔(obr. 3.14a)(obr. 3.14b)⇔⇔⇔⇔

SÍLA A MOMENT SÍLY - 18 -kde symbol ⇔ budeme dále používat pro ekvivalenci ať již z hlediska označování veličin taki z hlediska mechanické ekvivalence.Poznámka 1: Pokud se bude dále vyskytovat název moment bez bližšího vymezení (nebudeuváděn vztažný bod), bude se vždy jednat o moment silové dvojice.Poznámka2 : Samostatnou sílu nelze nahradit silovou dvojicí a samostatnou silovou dvojicinelze nahradit silou3.3.4 Souvislost momentů sílyVšechny dříve uvedené momenty mají stejnou fyzikální podstatu a stejný rozměr N.m.Rozdílná je však geometrická interpretace. V konečném výsledku otáčivý účinek vždyodpovídá působení silové dvojice. Souvislost mezi momentem síly k bodu, momentem k ose amomentem silové dvojice si ozřejmíme na příkladu dotahování matice klíčem (obr. 3.15).pɶF 1Obr. 3.15Míra mechanického působení síly F k bodu O je dána velikostí síly a délkou ramene síly(kolmou vzdáleností p nositelky síly od osy otáčení). Co však způsobuje otáčení klíče?Vzhledem k nezbytné vůli potřebné k zasunutí klíče na matici dojde při působení síly F naklíč na okrajích matice k bodovým kontaktům v místech A a B tj. ke vzniku kontaktních sil F 1a F 2jak je naznačeno na obr. 3.15. Na matici tedy v místech A a B působí silová dvojice otočivosti M k = F 1 d. Utažení šroubu tedy způsobuje tato silová dvojice. Vezmeme-limomentovou podmínku vzhledem k bodu B, pak vidíme, že souvislost mezi velikostí sil F 1 avelikostí zátěžné síly F je dána rovnicí M k = F 1 p d =F p. Jestliže se rameno síly F zvýší (např.prodloužením klíče pomocí trubky se rameno zvýší z hodnoty p na hodnotu pɶ ), pak jezřejmé, že při stejné velikosti síly F se zvýší i hodnota točivého účinku.Na matku tedy působí silová dvojice a ta je vektor volný v prostoru. Proto také připovolování matic na kole vozidla musíme začít s povolováním před vyheverováním vozidla(jinak se nám kolo protáčí v ose kola tj. v místě možného působení momentu silové dvojiceM k ).Při přenosu silových působení v technických zařízeních vzniká často moment silovédvojice mezi akční působící silou a silou reakční od rámu. Např. při otáčení volantu jednourukou vzniká reakční síla v uložení hřídele řízení a způsobuje namáhání uložení. Zároveňvzniklá reakční síla vytváří s akční sílou působící na volant nežádoucí silovou dvojici kteránamáhá hřídel volantu. Dalším zdrojem namáhání hřídele volantu je od momentu silovédvojice vzniklých tečných složek reakcí mezi koly a vozovkou, který je na hřídel volantupřenesen přes čepy kol a převodku řízení.F 2

SÍLA A MOMENT SÍLY - 19 -3.4 Věty o silách a momentechZ axiomů mechaniky a z pravidel vektorového počtu vyplývají o silách a momentech důležitévěty:V1 (Věta o posunutí síly)- Síla F je staticky ekvivalentní s každou silou stejné velikosti asmyslu ležící na nositelce n F . Jinými slovy- účinek síly na těleso se nezmění jestliže sepůsobiště síly libovolně posune po nositelce. Síla je tedy vektor volný na přímce.V2 (věta o 2 silách)- dvě síly jsou v rovnováze tehdy a jen tehdy, jestliže leží na společnénositelce, jsou stejně velké a jsou opačně orientované. Jinými slovy - síla F je v rovnovázes každou silou stejné velikosti a opačného smyslu, obě síly však musí ležet na společnénositelce. Tyto 2 síly vytváří soustavu nulového vektoru.V3 (věta o 3 silách)- 3 síly jsou v rovnováze tehdy a jen tehdy jestliže se jejich nositelkyprotínají v jednom bodě, síly leží v jedné rovině (jsou komplanární) a součet dvou sil je stejněvelký, ale opačně orientovaný než síla třetíV4 - K tělesu je možné přidat nebo ubrat rovnovážnou silovou soustavu aniž by se změniljeho pohybový stav.V5 - Každou sílu můžeme jednoznačně rozložit v prostoru do 3 nekomplanárních směrů(směry přitom nemusí být na sebe kolmé). V rovině můžeme každou sílu rozložit do 2různých směrůV6 (Varignonova věta 1) - Moment síly F vzhledem k libovolnému bodu je vektorovýmsoučtem momentů od jejích složek k témuž bodu (platí i pro neortogonální složky). Např.v případě kartézské soustavy platí M = r x F = r x i F + r x j F + r x k F( ) ( ) ( )A x y zV7 (Varignonova věta 2)- Moment výslednice centrální soustavy sil je roven vektorovémusoučtu momentů od jednotlivých silM = r x F = r x F = M∑∑A V i AiV8- Je-li moment síly k libovolnému bodu B roven M B, pak pro všechny body C přímky p,která je rovnoběžná s nositelkou síly F a prochází bodem B platí M = MBCV9 – Moment síly F k ose x je roven x-ové složce momentu síly F k libovolnému bodu B M = M pro B∈x . Vzhledem k tomu, že počátek O kartézskéležícím na x tj. platí ( B )soustavy je bodem ležícím na osách x, y, a z, platí pro něj M = M , M = M , M = M( ) ( ) ( )O x O y O zx y zV10- Moment silové dvojice je vektor volný v prostoruxxV11- Moment silové dvojice M k libovolné ose p je roven průmětu vektoru momentu silovédvojice do směru osy

SÍLA A MOMENT SÍLY - 20 -M = M .eppV12- Moment síly M p vzhledem k přímce p je nulový jestliže nositelka F přímku protíná neboje s ní rovnoběžnáV13- 2 silové dvojice jsou v rovnováze tehdy a jen tehdy, jestliže jejich vektory jsou stejněvelké, opačně orientované, a opačného smyslu (silové dvojice přitom nemusí ležetv rovnoběžných rovinách)