7 Reale Arbeitsprozessrechnung

7 Reale Arbeitsprozessrechnung
Bei der Füll- und Entleermethode, einer nulldimensionalen Methode, bei der die Prozessgrößen
nur von der Zeit, aber nicht vom Ort abhängen, werden die einzelnen Teilsysteme des
Motors, z. B.:
- Brennraum,
- Ansaug- und Abgasleitungen,
- Ventile und Klappen, sowie das
- Aufladesystem
physikalisch und mathematisch entweder durch die Ersatzsysteme
- Behälter, Leitungen oder
- Blenden
oder durch Kennfelder beschrieben.
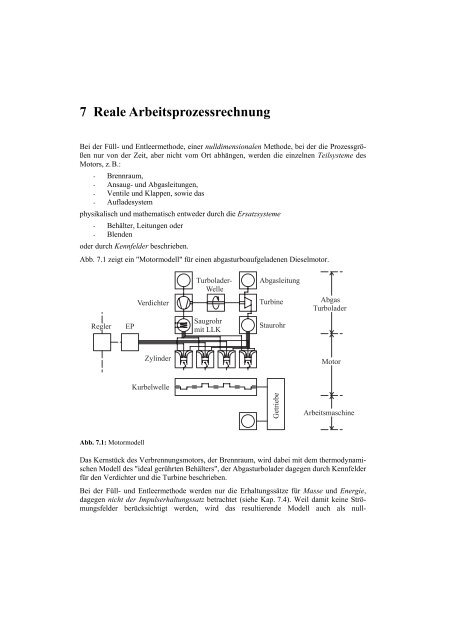
Abb. 7.1 zeigt ein "Motormodell" für einen abgasturboaufgeladenen Dieselmotor.
Regler EP
Abb. 7.1: Motormodell
Verdichter
Zylinder
Kurbelwelle
Turbolader-
Welle
Saugrohr
mit LLK
Abgasleitung
Turbine
Staurohr
Getriebe
Abgas
Turbolader
Motor
Arbeitsmaschine
Das Kernstück des Verbrennungsmotors, der Brennraum, wird dabei mit dem thermodynamischen
Modell des "ideal gerührten Behälters", der Abgasturbolader dagegen durch Kennfelder
für den Verdichter und die Turbine beschrieben.
Bei der Füll- und Entleermethode werden nur die Erhaltungssätze für Masse und Energie,
dagegen nicht der Impulserhaltungssatz betrachtet (siehe Kap. 7.4). Weil damit keine Strömungsfelder
berücksichtigt werden, wird das resultierende Modell auch als null-

7.1 Ein-Zonen-Zylinder-Modell
dimensionales, thermodynamisches Modell bezeichnet. Für einen allgemeinen Überblick sei
auf Ramos (1989) verwiesen.
Zur Beschreibung der Vorgänge in der Frischluft- und Abgasanlage von Saugmotoren (heute
fast nur noch Ottomotoren) müssen die Prozessgrößen mit Hilfe der eindimensionalen Gasdynamik
als Funktion der Zeit und des Ortes beschrieben werden. Derart komplexe Systeme
leben von der Dynamik der hin- und herlaufenden Druckwellen und dem Zusammenspiel
dieser Druckwellen mit den Ventilsteuerzeiten zur Erzielung einer möglichst hohen Füllung.
Die Saug- und Abgasanlage lässt sich dabei aus einer Vielzahl von Rohrstücken darstellen,
die über Rohrverzweigungen, Behälter, Blenden, Zylinder und eventuell über Strömungsmaschinen
verbunden sind (vgl. Kap. 7.4).
Das Kap. 7.5 geht speziell auf die Anforderungen zur Simulation von Aufladeaggregaten und
der Luftkühlung ein.
7.1 Ein-Zonen-Zylinder-Modell
7.1.1 Grundlagen
Abb. 7.2 zeigt den Brennraum eines Verbrennungsmotors. Dieser ist begrenzt von den Brennraumwänden,
dem Kolben und den Ventilen. Die Brennraumränder stellen gleichzeitig die
Systemgrenzen dar. Der gesamte Brennraum wird als ideal gerührter Behälter betrachtet,
wobei die Wärmefreisetzung durch die Verbrennung mit Hilfe eines Ersatzbrennverlaufs
beschrieben wird. Auf Mehr-Zonen-Modelle, mit denen man z. B. die NOx -Bildung im
Brennraum beschreiben kann, wird später näher eingegangen (vgl. Kap. 7.2).
pT e e�eRe dHe Systemgrenze
dm e
Abb. 7.2: Ein-Zonen-Zylinder-Modell
dmbb dHbb dU
dm
dQ B
dm B
n
pT
mVu
� R
dW
dHa dma pT a a�aRa dQ W
145

146
7 Reale Arbeitsprozessrechnung
Dabei ist zu beachten, dass sich als Folge der Kolbenbewegung das Volumen des Brennraums
mit der Zeit bzw. mit dem Kurbelwinkel kontinuierlich ändert, aber nicht notwendigerweise
auch die Masse im Brennraum. Bei der Betrachtung der Bilanzgleichungen im Brennraum
muss man zwischen den unterschiedlichen Konzepten der Kraftstoffeinbringung unterscheiden.
Während beim gemischansaugenden Ottomotor der Kraftstoff – sofern nicht mit einem
Wandfilmmodell gerechnet wird – proportional zur Frischluft angesaugt wird, wird beim
direkteinspritzenden Ottomotor der Brennstoff entweder während des geöffneten Einlassventils
(homogener Betrieb, Saughubeinspritzung) oder kurz vor der Zündung (geschichteter
Betrieb) eingespritzt. Der Kraftstoff muss dann im Brennraum aufbereitet bzw. verdampft
werden. Beim Dieselmotor wird der Kraftstoff direkt eingespritzt. Eine Verdampfung des
Kraftstoffes wird in der Regel nicht berücksichtigt (Ausnahme: Mehr-Zonen-Modelle mit
Kraftstoffzerfallsmodellen).
Die Massenbilanz für den Zylinder liefert für die Beschreibung aller oben genannter Möglichkeiten
zur Kraftstoffeinbringung
d mSys dm
m m m
e d a d d
BB Br.,
verd.
= + + +
. (7.1)
dt
dt
dt
dt
dt
Der in den Motor eintretende Massenstrom kann, wie bereits erwähnt, reine Luft, ein Luft-
Kraftstoffgemisch, ein Luft-Abgasgemisch oder eine Kombination von Luft, Kraftstoff und
Abgas sein.
Die Energiebilanz bzw. der 1. Hauptsatz der Thermodynamik liefert für den Zylinder unter
Vernachlässigung der kinetischen Energie
dESys
dU
dQB
dQW
dV
dme
dma
= = + − p + he
+ ha
+
dt
dt
dt
dt
dt
dt
dt
(7.2)
dm
dm
BB
Br.,
verd.
dQverd.
+ hBB
+
hBr.,
verd.
+ ,
dt
dt
dt
vgl. auch (2.30). Solange der Kraftstoff zwar in den Brennraum eingespritzt, jedoch noch
nicht verdampft ist, nimmt er ein so kleines Volumen ein, dass dies für das thermodynamische
System unerheblich ist. Der eingebrachte Kraftstoff wird für die Massen- und Energiebilanz
erst dann "wirksam", wenn er verdampft und damit gasförmig ist. Vor der Verdampfung
muss der Kraftstoff aufgeheizt werden, wozu dem Gas eine entsprechende Wärmemenge
entzogen wird. Ebenso verhält es sich mit der Aufheizung des Kraftstoffdampfes auf Gastemperatur.
Normalerweise werden diese Effekte im unteren Heizwert derart berücksichtigt, dass
die Verdampfungsenthalpie des Kraftstoffs (350-420 kJ/kg) zum unteren Heizwert addiert
wird. Gleiches gilt für die Rückkondensation von Kraftstoff und für den Wassergehalt in der
Luft, wenn das Gas stark expandiert wird (z. B. bei Laststeuerung durch frühes "Einlass
schließt").
Als unabhängige Variable können entweder die Zeit t oder der Kurbelwinkel ϕ gewählt
werden. In neueren Gleichungen wird meist der Zeit t der Vorrang gegeben. Für den Zusammenhang
zwischen der Zeit und dem Grad Kurbelwinkel gilt
ϕ = ω t
(7.3)
dϕ = ω dt
.

7.1 Ein-Zonen-Zylinder-Modell
Zur Lösung der Massen- und Energiebilanz benötigt man die bereits eingeführte thermische
Zustandsgleichung
pV = mRT . (7.4)
Zur Lösung dieses Gleichungssystems benötigt man noch Beziehungen für die Energiefreisetzung
durch die Verbrennung, ein so genanntes "Verbrennungsmodell", eine Beziehung für
die Wärmeübertragung zwischen dem Gasgemisch und den Brennraumwänden, ein so genanntes
"Wärmeübergangsmodell", sowie ein Ladungswechselmodell (z. B. Zwei-Zonen-
Modell bei 2-Takt-Motoren) und unter Umständen ein Verdampfungsmodell. Der Volumenverlauf
wird durch ein Kurbeltriebsmodell vorgegeben. Auf die einzelnen Teilmodelle wird
im Folgenden explizit eingegangen.
7.1.2 Mechanische Arbeit
Die an den Kolben abgegebene Leistung d W dt
kann aus dem Zylinderdruck und der Änderung
des Zylindervolumens berechnet werden
dW dV
dV
= − p = − pω
. (7.5)
dt
dt
dϕ
In Kap. 2.2.1 sind die geometrischen Zusammenhänge am Kurbeltrieb dargestellt. Der Kurbeltrieb
kann durch die geometrischen Größen Kurbelwellenradius r , Pleuellänge l , Exzentrizität
e und Zylinderdurchmesser D beschrieben werden, woraus sich die Volumenänderung
dV dϕ
bestimmen lässt.
7.1.3 Ermittlung des Massenstroms durch die Ventile / Ventilhubkurven
Im Ventilspalt kommt es zu einer Einschnürung der Strömung. Dies hat zur Folge, dass die
tatsächliche Querschnittsfläche kleiner ist als die geometrische. Infolge von Reibung in den
Kanälen ist der tatsächliche Massenstrom ebenfalls kleiner als der theoretische. Dieser Tatsache
trägt man durch die Einführung eines Durchflussbeiwertes
m&
tats.
µ ≡
(7.6)
m&
theo.
Rechnung.
Zur Ermittlung des Massenstromes durch ein Ventil bedient man sich der in Kap. 2.3.1 hergeleiteten
Durchflussfunktion. Dazu wird für die Ventile der tatsächliche Massenstrom in Abhängigkeit
vom Ventilhub an einem so genannten Blasprüfstand ermittelt und mit dem
theoretischen (siehe (2.37)) ins Verhältnis gesetzt
⎛ p ⎞
⎜ 2
m& theo = Ageo
p1
ρ 1 Ψ , κ ⎟ .
⎝ p1
⎠
Abb. 7.3 zeigt prinzipiell die Verhältnisse am Blasprüfstand. Der Durchflussbeiwert wird
dabei meist auf eine kreisrunde Fläche am Kanaleintritt bezogen. Da unterschiedliche Kreisprozessrechenprogramme
unterschiedliche Definitionen der Ventilöffnungsfläche besitzen, ist
147

148
7 Reale Arbeitsprozessrechnung
meistens eine entsprechende Umrechnung erforderlich. Dabei ist darauf zu achten, dass die
effektive Querschnittsfläche unabhängig von der Definition der Bezugsquerschnittsfläche für
die jeweilige Ventilstellung erhalten bleibt.
h V
� 2
Adapter
Abb. 7.3: Ermittlung der Durchflussbeiwerte am Blasprüfstand
A geo
� 1
� 1
Abb. 7.4 zeigt qualitativ die am Blasprüfstand ermittelten Durchflussbeiwerte in Abhängigkeit
vom Ventilhub.
Durchflussbeiwert µ
0.6
0.4
0.2
qualitativ, bezogen auf Ageo 0.0
0.0 3.0 6.0 9.0
Abb. 7.4: Durchflussbeiwerte µ = f ( hV
)
EV, einströmend
EV, ausströmend
AV, einströmend
AV, ausströmend
Ventilhub h V
Dabei erkennt man, dass sich für die unterschiedlichen Strömungsrichtungen an den Einlass-
und Auslassventilen unterschiedliche Durchflussbeiwerte einstellen. Die Hauptströmungsrichtung
für das Einlassventil ist "Einströmen". Es kann jedoch auch zu einem
Ausströmen aus dem Einlassventil kommen. Aufgrund der geometrischen Zusammenhänge
ist dieser Strömungsfall schlechter als der des Einströmens. Genauso verhält es sich für das
Auslassventil. Hier ist jedoch der Hauptströmungsfall "Ausströmen", woraus ein prinzipiell
schlechteres Strömungsverhalten resultiert.
Die Durchflussbeiwerte können entweder im stationären Versuch ermittelt oder mittels 3-D-
CFD-Codes berechnet werden, um bereits ohne konkrete Hardware Aussagen über die Qualität
von Kanälen machen zu können. Dabei werden die Kanalgeometrie und der Zylinder
nachgebildet und ein entsprechendes Druckgefälle an den Rändern angelegt. In diskreten
Stufen wird der Ventilhub verändert und der "tatsächliche" Massenstrom berechnet. Dieser
kann dann ebenso wie bei der Messung mit dem theoretischen ins Verhältnis gesetzt werden.

7.1 Ein-Zonen-Zylinder-Modell
Abb. 7.5 zeigt die Ventilerhebungskurven für einen konventionellen Ventiltrieb. Für die Arbeitsprozessrechnung
ist es ausreichend, die Ventilerhebungskurven in Schritten von 1 bis
5°KW bereitzustellen und zwischen den Stützpunkten linear zu interpolieren. Eine Phasenverschiebung
der Ventilöffnung wird über die so genannte Spreizung vorgegeben. Unter
Spreizung versteht man den Abstand des Maximums der Ventilerhebung vom Oberen Totpunkt
des Ladungswechsels. Besitzt eine Ventilerhebungskurve im Maximum ein Plateau
wird der "mittlere" Kurbelwinkelwert zur Definition der Spreizung verwendet. Trotz der
Tatsache, dass der Wert für die Auslassspreizung negativ berechnet werden müsste, wird
hierfür meist der Betrag des Wertes – also eine positive Zahl – angegeben.
Auslass-Spreizung
Ventilhub
LWOT
Einlass-Spreizung
Grad Kurbelwinkel
Abb. 7.5: Ventilerhebungskurven für einen mechanischen Ventiltrieb
In Abb. 7.5 sind zusätzlich noch die Ventilerhebungskurven für einen vollvariablen mechanischen
Ventiltrieb eingezeichnet, bei dem eine stufenlose Verstellung des Ventilhubes möglich
ist. Mit dieser Variabilität für einen quantitätsgeregelten Ottomotor ist eine Lastregelung ohne
Drosselklappe möglich, da über den Ventilhub der Durchfluss und damit die Frischgasmasse
eingestellt werden kann. Für den Niedriglastbereich müssen die Ventilhubabstufungen im
Bereich von Zehntel-Millimetern vorgegeben werden; ab ca. 3 mm reicht eine Vorgabe in
halben bis ganzen Millimeterschritten. Zwischenstufen werden dabei linear interpoliert. An
den Kurven für die Durchflussbeiwerte ändert sich für einen vollvariablen Ventiltrieb nichts,
da die Durchflussbeiwerte abhängig vom Ventilhub angegeben werden. Lediglich im Bereich
kleiner Ventilhübe empfiehlt sich auch hier eine feinere Rasterung.
Gänzlich anders ist das Verhalten von so genannten elektromechanischen Ventiltrieben für
die Simulation zu sehen. Beim elektromechanischen Ventiltrieb handelt es sich um einen
Einmassenschwinger, der an den jeweiligen Endlagen durch einen Magneten meist geregelt
angezogen und dann gehalten wird. Dabei wird idealerweise nur die Verlustenergie beim
Schwingen von einer Endlage zur anderen durch die Magnete zugeführt. Idealisiert ist der
Ventilhubverlauf beim elektromechanischen Ventiltrieb damit nur von der Zeit und nicht vom
Grad Kurbelwinkel abhängig. Für unterschiedliche Drehzahlen ergeben sich die in Abb. 7.6
dargestellten Verläufe für die Ventilerhebungen. In diesem Beispiel wird das Ventil sofort bei
Erreichen der unteren Endlage wieder nach oben bewegt und nicht in dieser Endlage gehalten.
Die Bewegungsdifferentialgleichung für den Einmassenschwinger lautet
m & x&
+ dx&
+ cx = F t)
+ F ( t)
+ F ( t)
+ F ( t)
. (7.7)
Einlassventilhub
Reib ( Magnet Ventilteller
Kleb
Nicht berücksichtigt sind ferner die so genannte Klebekräfte am Aktuator, die von dessen
thermischem Zustand und vom Vorhandensein von z. B. Öl abhängen. Für die in Abb. 7.6
149

150
7 Reale Arbeitsprozessrechnung
dargestellten Werte sind die Dämpfungskonstante und sämtliche äußeren Kräfte zu Null gesetzt
worden. Damit ergibt sich idealisiert als Lösung für die Differentialgleichung eine Kosinusfunktion
⎡1
1 ⎛ 2t
⎞⎤
x( t)
= xmax
⎢ − cos⎜
π ⎟⎥
mit 0 < t < τ . (7.8)
⎣2
2 ⎝ τ ⎠⎦
Ventilhub [mm]
9
8
7
6
5
4
3
2
1
0
1000
2000
3000
4000
5000
6000 min -1
0 30 60 90 120 150 180
Grad Kurbelwinkel
Abb. 7.6: Ventilerhebungskurven für einen elektromechanischen Ventiltrieb
Als Maß für eine Periodendauer dient die so genannte Flugzeit τ , die den Vorgang zwischen
dem Öffnen des Ventils bis zum Schließen ohne Halten des Ventils in der geöffneten Stellung
beschreibt. Auf eine ausführlichere Modellierung soll hier jedoch verzichtet werden.
7.1.4 Wärmeübergang im Zylinder
Die Beschreibung des Wärmeübergangs im Verbrennungsmotor stellt höchste Anforderungen
an die Modellierung und beruht meist nur auf einer globalen Betrachtung der sehr komplexen
Zusammenhänge. Der Wärmeübergang setzt sich aus einem konvektiven und einem Strahlungsanteil
zusammen
dQW dQα
dQε
= + . (7.9)
dt
dt
dt
Meist wird der Strahlungsanteil dQε dt
dem konvektiven Wärmeübergangskoeffizienten
zugeschlagen, obwohl die Maxima von dQα dt
und dQε dt
bezüglich des Kurbelwinkels
eigentlich phasenverschoben auftreten.
Ausgehend vom Newton´schen Ansatz gilt für die Beschreibung des Wandwärmestromes
dQW
= ∑α i Ai
( TW
, i − TGas
) . (7.10)
dt
i

7.1 Ein-Zonen-Zylinder-Modell
Dabei unterteilt man den Brennraum meist in drei Bereiche (vgl. Abb. 7.2):
- Kolben,
- Zylinderkopf und
- vom Kolben freigegebener Teil der Laufbüchse inkl. Kolbenrückstand und Feuersteg.
Die Ventile werden meist zum Zylinderkopf gerechnet oder bei sehr detaillierter Modellierung
als weiterer, eigener Bereich betrachtet. Die Flächen für den Kolben und den Zylinderkopf
sind meist größer als die Zylinderquerschnittsfläche, da diese z. B. die Dachform bei
einem ottomotorischen Brennverfahren oder die Kolbenmuldenform bei einem diesel- oder
ottomotorischen Brennverfahren beschreiben. Der vom Kolben freigegebene Teil der Laufbüchse
ergibt sich zu
A = A + A
+ Dπ
s ( ϕ)
. (7.11)
Büchse
Feuersteg
Kolbenrückstand
Die Zuordnung zwischen Kolbenweg s (ϕ)
und der Stellung der Kurbelwelle ist in Kap. 2.2.1
bereits erfolgt.
Die Berechnung des Wärmeübergangs mit Hilfe des Newton´schen Ansatzes und des Wärmeübergangskoeffizienten
setzt eine genaue Beschreibung der Gas- und Wandtemperaturen
voraus. Die mittlere Gastemperatur ergibt sich aus der örtlichen Mittelung der Gastemperatur
im Brennraum. Da das System Brennraum meist als ideal gerührter Behälter angesehen wird,
ist die mittlere Gastemperatur aus der Zustandsgleichung für ein ideales Gas leicht zu
bestimmen. Bei den jeweiligen Wandtemperaturen handelt es sich um die über ein Arbeitsspiel
gemittelte Wandinnentemperatur. Für den Kolben und den Zylinder werden meist örtlich
konstante Temperaturen angesetzt. Bei der Laufbüchse hängt der Ansatz der Wandtemperatur
stark vom Motortyp und von der Tatsache ab, ob die Büchse ganz vom Wassermantel
umgeben ist oder nur teilweise. Bei der Vorgabe der Temperatur für die Büchse unterteilt
man diese meist in mehrere Bereiche oder man gibt ein Temperaturprofil über der Büchsenlänge
an. Die Temperaturen kann man entweder aus Messungen ermitteln oder man kann für
stationäre Betriebspunkte einen einfachen, iterativen Ansatz zur Berechnung der Wandinnentemperatur
verwenden. Dazu ist jedoch die Kenntnis der Temperaturen in wenigstens einem
Betriebspunkt erforderlich. Für instationäre Berechnungen reichen beide Verfahren nicht
mehr aus, weshalb man sich hier eines konkreteren Wärmeleitungsmodells bedient, das die
thermischen Trägheiten der jeweiligen Wand berücksichtigt. Alle Modelle sind in Kap. 7.1.6
beschrieben.
Zur Berechnung von Wärmeübergangskoeffizienten werden meist halbempirische Ansätze
verwendet, da viele Einflussfaktoren nur durch Versuche herausgearbeitet werden können.
Als Einflussparameter werden deshalb äußere Größen verwendet, die den Betriebspunkt charakterisieren.
In diesem Abschnitt werden im Wesentlichen zwei Ansätze vorgestellt: Der
Ansatz von Woschni, der 1969 für Großdieselmotoren erarbeitet und kontinuierlich weiterentwickelt
wurde, und der von Bargende, der 1990 für Ottomotoren vorgestellt wurde.
Daneben existieren in der Literatur noch eine Vielzahl weiterer Ansätze z. B. von Hohenberg
(1980) und Kleinschmidt (1993), auf die hier jedoch nicht näher eingegangen werden kann.
151

152
7 Reale Arbeitsprozessrechnung
• Wärmeübergang nach Woschni
Das Modell von Woschni (hier 1970) geht von einer stationären, vollturbulenten Rohrströmung
aus. Für den dimensionslosen Wärmeübergangskoeffizienten, die Nußelt-Zahl, erhält
man aus einer Dimensionsanalyse die halbempirische Potenzgleichung
0, 8 0,
4
Nu = C Re Pr
mit der Nußelt-Zahl
(7.12)
α D
Nu = ,
λ
der Reynolds-Zahl
(7.13)
ρ w D
Re =
η
und der Prandtl-Zahl
(7.14)
η
Pr =
ρ a
. (7.15)
Betrachtet man das Gas im Brennraum als ideales Gas,
p
ρ = ,
RT
so folgt zunächst
(7.16)
0,
8
α D ⎛ p w D ⎞ 0,
4
= C ⎜
⎟ Pr
λ ⎝ RT
η ⎠
und daraus durch Umformung für den konvektiven Wärmeübergangskoeffizienten
0,
4
0,
2 0,
8 0,
8 Pr λ
C D p w
0,
8
( RT
η)
−
(7.17)
α = . (7.18)
Mit den Stoffwerten
x
;
y
λ ⎛ T ⎞ η ⎛ T ⎞
Pr = 0,
74;
= ⎜ ⎟ = ⎜ ⎟
⎜ T ⎟ ⎜ T ⎟
(7.19)
λ0
⎝ 0 ⎠ η0
⎝ 0 ⎠
und mit der Annahme, dass die charakteristische Geschwindigkeit w gleich der mittleren
Kolbengeschwindigkeit ist, also w ≡ cm
, erhält man weiter
* −0,
2 0,
8 0,
8 −r
= C D p cm
T
α mit r = 0 , 8(
1 + y)
− x . (7.20)
Durch Vergleich mit Messwerten wird der Exponent r für die Temperaturabhängigkeit zu
*
r = 0,
53 und die Konstante zu C = 127,
93 bestimmt. Für gefeuerte Motoren wird zudem
eine Modifikation der charakteristischen Geschwindigkeit eingeführt, welche die Veränderung
des Wärmeübergangs infolge der Verbrennung berücksichtigen soll. Damit erhält man

7.1 Ein-Zonen-Zylinder-Modell
mit
⎡ ⎤
−0,
2 0,
8 0,
8 −0,
53 W
α = 127,
93 D p w T ⎢ ⎥
(7.21)
2
⎢⎣
m K ⎥⎦
w = C
1
c
Vh
T1
m + C2
( p − p0
)
p
1441V
41
24443
Verbrennungsglied
153
(7.22)
und p 1 , T1,
V1
bei Verdichtungsbeginn, d. h. bei "Einlass schließt". Für die Konstanten C 1
und C 2 erhält man durch Anpassung an Messwerte
⎧
cu
⎪6,
18 + 0,
417 : Ladungswechsel
⎪
cm
C 1 = ⎨
(7.23)
⎪
cu
2,
28 + 0,
308 : Verdichtung
/ Expansion
⎪
⎩
cm
⎧ −3
⎡ m ⎤
⎪6,
22⋅10
⎢ ⎥:
Vorkammer − Motor
⎪ ⎣s
K ⎦
C 2 = ⎨
. (7.24)
⎪ −3
⎡ m ⎤
⎪
3,
24⋅10
⎢ ⎥ : DI − Motor
⎩ ⎣s
K ⎦
Für den Einlassdrall c u cm
wird der Gültigkeitsbereich mit 0 ≤ c u cm
≤ 3 angegeben. Der
Drall wird im stationären Strömungsversuch auf dem Blasprüfstand mit der Methode nach
Tipelmann oder mit der Flügelrad-Methode ermittelt. Dabei wird ein Flügelrad mit dem
Durchmesser d im Abstand von 100 mm unterhalb des Zylinderkopfes in der Zylinderlaufbuchse
angeordnet. Die Strömung durch das Einlassventil wird dabei so eingestellt, dass
dieses Flügelrad mit der mittleren Kolbengeschwindigkeit c m angeströmt wird. Mit der zu
messenden Drehzahl n d des Flügelrades erhält man entsprechend
cu = Dπ
nd
(7.25)
die Umfangsgeschwindigkeit und damit den Drall.
Abhängig von den jeweiligen Phasen eines Arbeitsspieles werden einige Terme bzw. Parameter
in der Wärmeübergangsgleichung verändert. Dies führt zum Beispiel beim Übergang
zwischen Expansion und Ladungswechsel beim Öffnen des Auslassventils zu einem Sprung
in der Konstanten C 1.
Ebenso ist der Term mit der Konstanten C 2 nur nach dem Beginn der
Verbrennung gültig. Hier ist jedoch der Übergang zwischen der Kompressionsphase und der
Verbrennung durch den Term ( p − p0
) fließend.
Mit dem Term ( p − p0
) wird die Differenz zwischen dem Zylinderdruck bei Verbrennung
und dem Zylinderdruck im Schleppbetrieb angegeben. Der Druck p 0 kann dann über eine
Polytropenbeziehung aus dem Zylindervolumen berechnet werden. Die Bestimmung des
Polytropenexponenten n geschieht kurz vor der Verbrennung, indem die Polytropenexponenten
der z. B. letzten 10°KW vor Verbrennung gemittelt werden. Für p 0 ergibt sich dann

154
n
7 Reale Arbeitsprozessrechnung
⎛ V ⎞
v Verbr
p p ⎜ . . ⎟
0 ( ϕ ) = v.
Verbr.
. (7.26)
⎜V
⎟
⎝ Zyl.
( ϕ)
⎠
Die Abb. 7.7 zeigt ein Beispiel für den Wandwärmestrom an einem turboaufgeladenen Dieselmotor
bei einer Drehzahl von 2.000 U/min und einer effektiven Last von 2 bar.
Zylinderdruck
[bar]
alpha
[kW/m K]
2
Wärmestrom
[J/°KW]
Temperatur [K]
80 2000 80
2000
60 1500 60
1500
40 1000 40
1000
20
0
500
0
20
0
500
0
3 3
2 2
Zylinderdruck
[bar]
alpha
[kW/m K]
1 1
0 0
4 4
1 1
0 0
300 350 400 450 300 350 400 450
Kurbelwinkel [Grad] Kurbelwinkel [Grad]
2
3 3
Wärmestrom
[J/°KW]
2 2
Abb. 7.7: Wärmeübergang in einem turboaufgeladenen Dieselmotor, Brennbeginn 355°KW (links)
bzw. 368°KW (rechts)
Im unteren Teil des Diagramms sind die Wärmeströme von Kolben, Zylinderkopf und Büchse
sowie der Gesamtwärmestrom dargestellt. Darüber sind die Wärmeübergangskoeffizienten
nach Woschni sowie die Massenmitteltemperatur und der Druck im Zylinder dargestellt. Im
linken Teil ist ein Brennbeginn von 355°KW und im rechten Teil ein Brennbeginn von
368°KW aufgenommen. Hierbei ist zu erkennen, dass der vom Druck und von der Temperatur
abhängige Wärmeübergangskoeffizient bei späterem Brennbeginn deutlich kleiner ist.
• Modifikationen an der Wärmeübergangsgleichung nach Woschni
Untersuchungen zum Wärmeübergang von Kolesa (1987) bei isolierten Brennraumwänden
haben ergeben, dass der Wandwärmeübergangskoeffizient bei Wandtemperaturen über 600 K
stark ansteigt. Für die Konstante C 2 hat Schwarz (1993) eine stetige Funktion entwickelt
⎪⎧
C2
für T < 525 K
*
W
C 2 = ⎨
−6
(7.27)
⎪⎩ C2
+ 23⋅10
( TW
− 525)
für TW
≥ 525 K.
Die mit dem Verbrennungsglied in der Gleichung nach Woschni korrigierte Geschwindigkeit
liefert für geschleppte Motoren und im unteren Lastbereich jedoch zu geringe Werte, wie
Temperatur [K]

7.1 Ein-Zonen-Zylinder-Modell
Huber (1990) gezeigt hat. Deshalb wurde die Wärmeübergangsgleichung für Niedriglast
korrigiert. Für
2
⎡ Vc
⎤ −0,
2 Vh
T1
2C1 cm
⎢ ⎥ pmi
≥ C2
( p − p0
)
⎣V
( ϕ)
⎦
p1
V1
(7.28)
gilt
⎡
2
⎛ V ⎤
⎢ c ⎞ −0, 2
w = C1
cm
1 + 2⎜
⎟ pmi
⎥ .
⎢
⎥
⎣
⎝ V ⎠
⎦
(7.29)
Ferner gilt: p mi
= 1 für p mi
≤ 1.
Zusätzliche Untersuchungen zum Wärmeübergangskoeffizienten – insbesondere zur Isolationswirkung
von Brennraumwandanlagerungen (Ruß, Ölkoks) – wurden von Vogel (1995)
durchgeführt. Aus diesen Untersuchungen resultieren weiterführende Änderungen der von
Huber modifizierten Gleichung. Für
2
⎡ Vc
⎤ Vh
T1
2C1 cm
⎢ ⎥ C3
≥ C2
( p − p0
)
⎣V
( ϕ)
⎦ p1
V1
(7.30)
gilt
⎡
2
⎛V
⎤
⎢ c ⎞
w = C1
cm
1 + 2⎜
⎟ C3
⎥ .
⎢
⎥
⎣
⎝ V ⎠
⎦
(7.31)
Die Konstante C 2 für direkteinspritzende Dieselmotoren wird in ihrem Gültigkeitsbereich
für Benzin-Ottomotoren erweitert
C 2
−3
= 3,
24⋅10
⎡ m ⎤
⎢ ⎥
⎣s
K ⎦
: DI-Motor, Ottomotor (Benzin).
Als neue Konstanten werden eingeführt:
C 2
−3
= 4⋅10
⎡ m ⎤
⎢ ⎥
⎣s
K ⎦
: Ottomotor (Methanol),
C 3 = 0,
8
: für Benzin,
C 3 = 1,
0
: für Methanol und
C 3
−0,
65λ
= 1 − 1,
2e
: für Diesel.
Bei mittelschnelllaufenden Großdieselmotoren ergeben sich z. T. Abweichungen bei der Berechnung
der Abgastemperatur gegenüber der Messung von ca. 20 K. Die zu gering berechnete
Abgastemperatur führt zu einer zu niedrigen Enthalpie an der Turbine und damit zu einem
geringfügig zu niedrigen Ladedruck. Für die Auslegung der Großdieselmotoren ist dies jedoch
entscheidend, da diese meist auf einen stationären Betriebspunkt optimiert sind. Aus
diesem Grunde hat Gerstle (1999) den Wärmeübergang nach Woschni für den Ladungswechsel
modifiziert. Die Konstante C 1 gilt dabei über den Punkt des Auslassöffnens hinaus, bis
155