Structural Design and Response in Collision and Grounding

More documents

Recommendations

Info

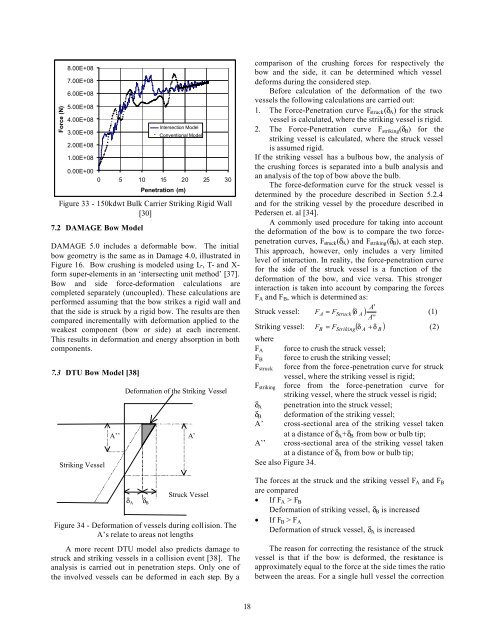
Force (N)8.00E+087.00E+086.00E+085.00E+084.00E+083.00E+082.00E+081.00E+08Intersection ModelConventional Model0.00E+000 5 10 15 20 25 30Penetration (m)Figure 33 - 150kdwt Bulk Carrier Striking Rigid Wall[30]7.2 DAMAGE Bow ModelDAMAGE 5.0 includes a deformable bow. The initialbow geometry is the same as in Damage 4.0, illustrated inFigure 16. Bow crushing is modeled using L-, T- and X-form super-elements in an ‘intersecting unit method’ [37].Bow and side force-deformation calculations arecompleted separately (uncoupled). These calculations areperformed assuming that the bow strikes a rigid wall andthat the side is struck by a rigid bow. The results are thencompared incrementally with deformation applied to theweakest component (bow or side) at each increment.This results in deformation and energy absorption in bothcomponents.7.3 DTU Bow Model [38]Striking VesselDeformation of the Striking VesselA’’ A’comparison of the crushing forces for respectively thebow and the side, it can be determined which vesseldeforms during the considered step.Before calculation of the deformation of the twovessels the following calculations are carried out:1. The Force-Penetration curve F struck (δ A ) for the struckvessel is calculated, where the striking vessel is rigid.2. The Force-Penetration curve F striking (δ B ) for thestriking vessel is calculated, where the struck vesselis assumed rigid.If the striking vessel has a bulbous bow, the analysis ofthe crushing forces is separated into a bulb analysis andan analysis of the top of bow above the bulb.The force-deformation curve for the struck vessel isdetermined by the procedure described in Section 5.2.4and for the striking vessel by the procedure described inPedersen et. al [34].A commonly used procedure for taking into accountthe deformation of the bow is to compare the two forcepenetrationcurves, F struck (δ A ) and F striking (δ B ), at each step.This approach, however, only includes a very limitedlevel of interaction. In reality, the force-penetration curvefor the side of the struck vessel is a function of thedeformation of the bow, and vice versa. This strongerinteraction is taken into account by comparing the forcesF A and F B , which is determined as:A'Struck vessel: FA= FStruck( δ A )(1)A''F = δ + δ(2)Striking vessel: ( )B F StrikingwhereF A force to crush the struck vessel;F B force to crush the striking vessel;F struck force from the force-penetration curve for struckvessel, where the striking vessel is rigid;F striking force from the force-penetration curve forstriking vessel, where the struck vessel is rigid;δ A penetration into the struck vessel;δ B deformation of the striking vessel;A’ cross-sectional area of the striking vessel takenat a distance of δ A +δ B from bow or bulb tip;A’’ cross-sectional area of the striking vessel takenat a distance of δ A from bow or bulb tip;See also Figure 34.ABδ Aδ BStruck VesselFigure 34 - Deformation of vessels during collision. TheA’s relate to areas not lengthsA more recent DTU model also predicts damage tostruck and striking vessels in a collision event [38]. Theanalysis is carried out in penetration steps. Only one ofthe involved vessels can be deformed in each step. By aThe forces at the struck and the striking vessel F A and F Bare compared• If F A > F BDeformation of striking vessel, δ B is increased• If F B > F ADeformation of struck vessel, δ A is increasedThe reason for correcting the resistance of the struckvessel is that if the bow is deformed, the resistance isapproximately equal to the force at the side times the ratiobetween the areas. For a single hull vessel the correction18
will have nearly no influence, but for a double hull vessel,there will be some corrections when the bow penetratesthe inner side. See Figure 34.When the deformation patterns of the struck and thestriking vessel are known, the total absorbed energy canbe calculated and compared with the energy calculated bythe external dynamics. See Pedersen and Zhang [29].present, and the overwhelming majority of single-skinneddesigns are longitudinally stiffened. OPA ’90 mandatesthe use of double-skinned tanker designs, Figure 36 [39].8 STRUCTURAL DESIGN FOR COLLISIONAND GROUNDINGThe function of a tank vessel’s structural system may beviewed from the standpoints of normal operation andcasualty operation. In providing adequate resistance fornormal operations, the objective in structural design is tomaintain structural integrity of the hull girder, ofbulkheads, decks, etc., and of plating, stiffeners anddetails. Other considerations relate to vessel size,complexity and heaviness of structure, producibility andmaintainability. In terms of casualty operations, theobjective is to maintain vessel integrity and to protectcargo, or conversely to protect the environment from oilpollution in case of a casualty. In this case the primaryconsiderations should include:1. Resistance to fire and explosion damage and itscontainment,2. Resistance to collision and grounding damage,3. Containment of petroleum outflow if damage doesoccur, and4. Maintenance of sufficient residual strength afterdamage in order to permit salvage and rescueoperation and to minimize further damage andspilling of oil.Figure 36 - Double-Hull Tanker [39]The Marine Board of the National Research Councilhas recently convened a "Committee on EvaluatingAlternative Tanker Designs". The committee is toestablish, for the first time, a rational methodology toevaluate alternatives to the double hull. The US CoastGuard is sponsoring this Committee, and its report isexpected in the first quarter of 2001.The emphasis of new and proposed requirements forreducing the probability of oil cargo outflow has been onthe subdivision of cargo spaces. The impact of hullstructure on the reduction of outflow has had more limitedattention. The complexity of determining the contributionof structure to cargo protection and the unpredictability ofstructural response under the variety of potential damagescenarios have no doubt contributed to this set ofcircumstances.The following subsections address the subject ofvessel structural design characteristics for collision,grounding and bow impact. The intent is to consider whathas been learned from analytical studies regardingstructural design features that may suggest futuremodifications and alternatives to enhance resistance tocargo outflow.8.1 Collisions8.1.1 Analytical Indications – Struck ShipFigure 35 - Single-Hull Tanker [39]Tank vessels have traditionally been designed assingle-skinned hulls, Figure 35 [39]. Depending on thesize of the vessel, longitudinal bulkheads are oftenThe sequence of structural events during a collision variesaccording to the nature of the collision and vessel design.Figures 37 and 38 [24] provide general flow diagramsrepresenting the phenomena for single and double hulltankers. This information is useful in identifying wheregreater resistance can be addressed.19
Page 1 and 2: Brown, A.J., Tikka, K., Daidola, J.
Page 3 and 4: 3 PROBABILISTIC FRAMEWORKFigure 2 i
Page 5 and 6: 4.2.2 Method by Wang [15]Dr. Wang d
Page 7 and 8: damage results. Surprisingly, the t
Page 9 and 10: ybeginning of time step nStriking S
Page 11 and 12: location, COG, and detailed structu
Page 13: Ship Type150,000 dwtbulk carrierLen
Page 16 and 17: 6.2 DATA FOR MODEL VALIDATIONThe se
Page 20 and 21: Figure 37 - Macro flow diagram for
Page 22 and 23: enhance resistance to collision. Th
Page 24 and 25: Figure 42 - Load versus lateral ind
Page 26 and 27: Accidental Grounding and Collision

Structural Design and Response in Collision and Grounding

Create successful ePaper yourself

Delete template?

Save as template?