2. movimiento ondulatorio - Tecnun

2. Movimiento Ondulatorio
2. MOVIMIENTO ONDULATORIO
Cuando golpeamos una campana ó encendemos una radio, el sonido se oye en
puntos distantes de la campana ó de la radio. El sonido se ha transmitido a través del
aire. Si estamos en la playa y un bote pasa velozmente a cierta distancia de la orilla
sentimos al cabo del tiempo la onda producida por su movimiento. Cuando se
enciende la lámpara del cuarto, éste se ilumina. Aunque el mecanismo físico puede
ser diferente para cada uno de los procesos mencionados todos ellos tienen una
característica en común, son perturbaciones físicas producidas en un punto del
espacio que se propagan a través del mismo y que se reciben en otro punto. Todos
estos procesos son ejemplos del movimiento ondulatorio cuya característica esencial
es que en él se transmite una propiedad de un lugar a otro a través de un medio, pero
el medio en sí mismo no se traslada, es decir no se traslada masa sino energía.
2.1 Descripción matemática del movimiento ondulatorio
Pasemos a describir matemáticamente este fenómeno. Consideremos una
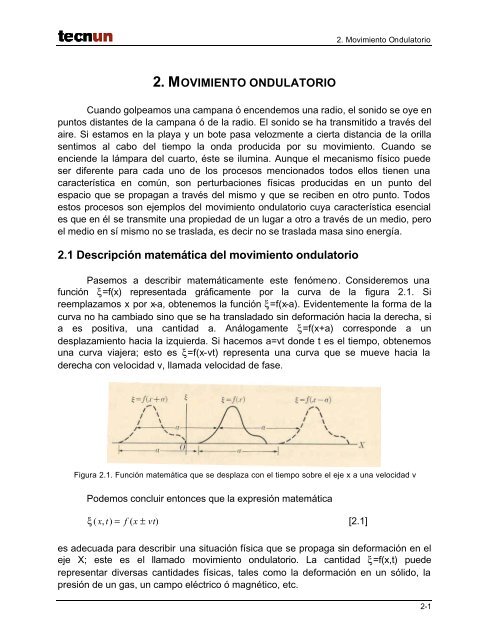
función ξ=f(x) representada gráficamente por la curva de la figura 2.1. Si
reemplazamos x por x-a, obtenemos la función ξ=f(x-a). Evidentemente la forma de la
curva no ha cambiado sino que se ha transladado sin deformación hacia la derecha, si
a es positiva, una cantidad a. Análogamente ξ=f(x+a) corresponde a un
desplazamiento hacia la izquierda. Si hacemos a=vt donde t es el tiempo, obtenemos
una curva viajera; esto es ξ=f(x-vt) representa una curva que se mueve hacia la
derecha con velocidad v, llamada velocidad de fase.
Figura 2.1. Función matemática que se desplaza con el tiempo sobre el eje x a una velocidad v
Podemos concluir entonces que la expresión matemática
ξ ( x , t)
= f ( x ± vt)
[2.1]
es adecuada para describir una situación física que se propaga sin deformación en el
eje X; este es el llamado movimiento ondulatorio. La cantidad ξ=f(x,t) puede
representar diversas cantidades físicas, tales como la deformación en un sólido, la
presión de un gas, un campo eléctrico ó magnético, etc.
2-1

2. Movimiento Ondulatorio
Figura 2.2. Ondas superficiales en el agua
combinación de ondas transversales y longitudinales
Figura 2.3.a. Onda continua ocupando todo el eje x
Figura 2.3.b. Onda limitada a una zona del espacio
denominada tren de ondas ó pulso
En una onda la perturbación
puede ser perpendicular ó paralela a la
dirección de propagación. Según esto
distinguimos entre ondas transversales,
donde la perturbación física es
perpendicular a la dirección de
propagación, caso del campo
electromagnético, y ondas
longitudinales con la perturbación
paralela a la dirección de propagación,
caso por ejemplo del sonido. Existen
casos de movimientos ondulatorios
combinación de transversales y
longitudinales, como por ejemplo las
ondas superficiales del agua tal y como
se muestra en la figura 2.2. Podemos
tambien tener una onda que ocupa todo
el eje X, denominada onda continua, ó
una onda que empieza y acaba en
puntos determinados del espacio que
se denomina tren de ondas ó pulso,
esquematizadas ambas en la figura 2.3.
2.2 Movimiento ondulatorio armónico
Un caso especialmente interesante es aquel en el que ξ=f(x,t) es una funcional
sinusoidal ó armónica tal como
ξ ( x,
t)
= ξ0senk(
x − vt)
[2.2]
donde ξ 0 es la amplitud y la cantidad k tiene un significado especial. Reemplazando el
valor de x por x+ 2 π
k
obtenemos para ξ=f(x,t) el mismo valor
2π
2π
ξ ( x + − vt)
= ξ0senk(
x + − vt)
= ξ0sen(
k(
x − vt)
+ 2π
) =
k
k
= ξ ( x − vt)
[2.3]
es decir
2π
λ = [2.4]
k
2-2

2. Movimiento Ondulatorio
es el periodo espacial de la curva 2.4
que representa la ecuación [2.2]. Esto
es, la curva se repite cada longitud λ que
recibe el nombre de longitud de onda.
Entonces la cantidad k = 2π λ
representa
el número de longitudes de onda en la
distancia 2π y se denomina número de
onda. Por consiguiente [2.2] representa
Figura 2.4. Movimiento ondulatorio armónico
una onda sinusoidal de longitud de onda
λ propagándose hacia la derecha según el eje X con velocidad v tal y como se
muestra en la figura 2.5 donde se observa como un punto de fase constante, en este
caso notado como B, se desplaza hacia la derecha del eje X.
Figura 2.5. Propagación de la onda según el eje X con una velocidad v. Se observa como un punto de
fase constante, en este caso notado como B, recorre una distancia igual a una longitud de onda λ en un
tiempo f -1 .
2-3

2. Movimiento Ondulatorio
La ecuación [2.2] puede escribirse también en la forma
ξ ( x,
t)
= ξ0sen(
kx−
ωt)
[2.5]
donde
ω
2πv
= kv =
[2.6]
λ
da la frecuencia angular de la onda. Puesto que sabemos que
ω = 2πf
donde f es la
frecuencia con la cual la perturbación física varía en cada punto llegamos a la relación
λ f = v
[2.7]
que liga la longitud de onda con la frecuencia y la velocidad de propagación del
movimiento ondulatorio. Es decir la onda sinusoidal se propaga, puntos de fase
constante, una longitud λ en un tiempo f -1 .
En el capítulo anterior vimos que según el teorema de Fourier, cualquier
movimiento periódico se puede expresar como superposición de movimientos
armónicos simples de frecuencias ω, 2ω, 3ω,….., nω,… El mismo resultado se aplica
al movimiento ondulatorio periódico de tal forma que el movimiento ondulatorio
descrito por ξ = f ( x − vt)
puede expresarse como
ξ = f ( x − vt)
= a
+ a
n
cos n(
kx−
ωt)
+ .... + b sen(
kx −ωt)
+ b sen2(
kx − ωt)
+ ...... +
+ b senn(
kx−
ωt)
+ ....
n
0
+ a
1
cos( kx −ωt)
+ a
1
2
cos2ω
( kx − vt)
+ ...... +
2
[2.8]
lo cual indica que cualquier movimiento ondulatorio periódico se puede expresar como
una superposición de movimientos ondulatorios armónicos de frecuencias ω, 2ω, ….,
nω,.. y longitudes de onda λ,λ/2,…, λ/n,… Debido a este resultado es importante
comprender el movimiento ondulatorio armónico a fín de entender el movimiento
ondulatorio en general.
2.3 Ecuación diferencial del movimiento ondulatorio
El proceso físico que gobierna el movimiento ondulatorio estará regido por
leyes dinámicas, características de cada proceso, y que pueden expresarse en forma
de ecuaciones diferenciales, tal y como ya vimos para el movimiento oscilatorio. Nos
proponemos en este apartado encontrar una ecuación diferencial aplicable a todo tipo
de movimiento ondulatorio de tal forma que cada vez que
2-4

2. Movimiento Ondulatorio
veamos que una magnitud física satisface tal ecuación podemos estar seguros que se
propaga a través del espacio con velocidad definida y sin distorsión.
La ecuación diferencial que describe el movimiento ondulatorio que se propaga
a una velocidad v y sin distorsión según las direcciones –X ó +X es
2
∂ ξ
2
∂t
= v
2
2
∂ ξ
2
∂x
[2.9]
La solución general de esta ecuación tiene la forma
ξ ( x , t)
= f1(
x − vt)
+ f2(
x + vt)
[2.10]
que son dos movimientos ondulatorios que se propagan en la misma dirección pero en
sentidos opuestos. Verificando este hecho para el caso concreto de una onda
armónica ξ = ξ0senk(
x − vt)
∂ξ
∂x
∂ξ
∂t
2
∂ ξ 2
= kξ0
cos k(
x − vt),
= −k
ξ0senk(
x − vt);
2
∂x
2
∂ ξ 2 2
= −kvξ0
cos k(
x − vt),
= −k
v ξ0senk(
x − vt)
2
∂t
[2.11]
cumpliéndose la ecuación diferencial [2.9].
2.4 Velocidades de ondas en medios específicos
A fín de comprender mejor las ideas fundamentales del movimiento ondulatorio
en este apartado discutiremos ciertos tipos de ondas más o menos familiares
2.4.1 Ondas transversales en una cuerda. Consideremos el caso de una cuerda
sometida a una tensión T. En condiciones de equilibrio la cuerda está en línea recta.
Desplazemos la cuerda perpendicularmente a su longitud una pequeña cantidad como
se muestra en la figura 2.6. La porción AB de la cuerda de longitud dx se desplaza de
su posición de equilibrio una distancia ξ. En cada extremo del segmento actúa una
fuerza tangencial T. Debido a la curvatura de la cuerda, estas fuerzas no son
directamente opuestas
La fuerza resultante según el eje Y sobre el segmento AB de la cuerda es
F y
= T ( senα´
−senα
)
[2.12]
2-5

2. Movimiento Ondulatorio
Figura 2.6. Diagrama de fuerzas en una cuerda desplazada perpendicularmente a su longitud
Si la curvatura de la cuerda no es muy grande α y α´ son pequeños y sus
senos pueden reemplazarse por sus tangentes. De modo que la fuerza hacia arriba es
∂
F y
= T ( tgα
´ −tgα
) = T ( tgα
) dx
[2.13]
∂x
y dado que tgα es la pendiente de la curva formada por la cuerda que es igual a
obtenemos
∂ξ
∂x
2
∂ ξ
= T
∂x
F y 2
dx
[2.14]
y utilizando la 2º ley de Newton, siendo µ la densidad lineal de la cuerda y la
2
aceleración
∂ ξ
2
∂t
2
2
∂ ξ ∂ ξ
( µ dx)
= T dx
es decir
2
2
∂t
∂x
2
∂ ξ
2
∂t
T
=
µ
2
∂ ξ
2
∂x
[2.15]
La perturbacion, que cumple la ecuación diferencial del movimiento ondulatorio,
se propaga de forma transversal a lo largo de la misma, y siempre que la amplitud del
desplazamiento sea pequeña, con una velocidad
T
v = [2.16]
µ
2-6

2. Movimiento Ondulatorio
2.4.2 Ondas elásticas longitudinales en una barra. Consideremos una barra de
sección transversal uniforme A, sujeta a una fuerza F según su eje. El esfuerzo normal
ó tensión se define como σ = F A
relacionada con la deformación unitaria ε = ∆l l
por
la ley de Hooke σ = Eε
donde E es el modulo de Young del material que forma la
barra. Bajo la acción de F, la sección de la barra experimenta un desplazamiento ξ
paralelo al eje, es decir tenemos una onda longitudinal. Si este desplazamiento es el
mismo en todos los puntos, no se produce deformación de la barra sino simplemente
un desplazamiento en conjunto de la misma. Estamos interesados en el caso en el
que se produce deformación, es decir ξ varía a lo largo de la barra dependiendo su
valor de x. Consideremos 2 secciones A, sobre la que actúa una fuerza F, y A´, sobre
la que actúa una fuerza F´,separadas una distancia dx en el estado de equilibrio tal y
como se muestra en la figura 2.7.
Figura 2.7. Diagrama de fuerzas en una barra sometida a una deformación longitudinal
Cuando la fuerza F se manifiesta, la sección A se desplaza la distancia ξ y la
sección A´ la distancia ξ´. Luego la separación entre A y A´ en el estado de
deformación vale
dx + ( ξ´
−ξ
) = dx + dξ
[2.17]
Por tanto la deformación unitaria de la barra en dx es
∂
ε = ξ
[2.18]
∂x
Introduciendo este valor en la ley de Hooke obtenemos
∂ξ
F = EA
∂x
[2.19]
La fuerza neta que actúa sobre esta sección de barra, de masa dm=ρAdx,
∂F
siendo ρ la densidad del material, es dF=F-F´= dx . La aceleración de esta masa
∂x
2-7

2. Movimiento Ondulatorio
2
∂ ξ
es igual a
2 . Por tanto, la 2º ley de Newton aplicada a esta sección de barra
∂t
queda
∂F
∂x
2
∂ ξ
= ρ A
[2.20]
2
∂t
que combinada con la ecuación [2.19] da lugar a
2
∂ ξ
2
∂t
=
2
E ∂ ξ
2
ρ ∂x
[2.21]
con lo que la velocidad de propagación de las ondas elásticas longitudinales en la
barra es igual a
E
v = [2.22]
ρ
2.5 Energía e intensidad de una onda
En todas las ondas analizadas hasta ahora, la propagación de la onda da lugar
a un movimiento de partículas (átomos ó moléculas) del medio a través del cual viaja
la onda, pero en promedio las partículas permanecen en su posición de equilibrio.
Como ya ha sido mencionado, en un movimiento ondulatorio no es materia lo que se
propaga sino una condición física descrita en términos de energía y cantidad de
movimiento. Se afirma entonces que cuando una onda se propaga a través de un
medio transmite energía y cantidad de movimiento.
Consideremos el caso de las ondas armónicas donde el desplazamiento del
equilibrio viene dado por ξ = ξ0sen(
kx − wt)
. Para una posición x dada tenemos la
ecuación de un oscilador armónico. Recordando el resultado de la energía total de un
oscilador y utilizando la densidad ρ en lugar de la masa total tendremos que la energía
por unidad de volumen ó densidad de energía u asociada al movimiento ondulatorio
viene dada por la ecuación
1 2 2
u = ρω ξ0
[2.23]
2
y se mide en Jm -3 . El transporte de energía por una onda se describe habitualmente
en función de la intensidad de la onda I definida como la energía que fluye por unidad
de tiempo a través de un área unitaria perpendicular a la dirección de propagación
2-8

2. Movimiento Ondulatorio
I = uv
[2.24]
donde v es la velocidad de propagación de la onda. La intensidad de la onda se
expresa en Js -1 m -2 =W m -2 , es decir equivalente a potencia por unidad de área. Para
una onda armónica y utilizando [2.23] llegamos a
I
1 2 2
= ρω ξ0
v
[2.25]
2
indicando que en una onda armónica, la intensidad es proporcional al cuadrado de la
amplitud.
2.6 Ondas en dos y tres dimensiones
Figura 2.8. Onda en tres dimensiones
propagándose según el eje X
Aunque ξ = f ( x − vt)
representa
un movimiento ondulatorio que se
propaga según el eje X, no tenemos
necesariamente que interpretarla como
una onda concentrada según ese eje. Si
la perturbación física descrita por ξ se
extiende sobre todo el espacio, tenemos
que en el tiempo t dado, ξ toma el mismo
valor para todos los puntos r de abcisa x.
Pero x=cte representa un plano
perpendicular al eje X, como se muestra
en la figura 2.8, denominado frente de
onda. Por lo tanto ξ ( r,
t)
= f ( x − vt)
describe en tres dimensiones una onda
plana, frente de ondas plano, que se
propaga paralela al eje X. Observemos
que lo característico de una onda plana
es la dirección de propagación que se
indica con un vector u perpendicular al
plano de la onda. Si r es el vector de
posición de cualquier punto P del frente
de ondas, tenemos que x=u.r y podemos
escribir
ξ ( r,
t)
= f ( u.
r − vt)
[2.26]
Figura 2.9. Onda en tres dimensiones
propagándose según una dirección arbitraria
Cualquiera que sea la dirección de
u, figura 2.9, la cantidad u.r es siempre la
2-9

2. Movimiento Ondulatorio
distancia medida desde el origen O según la dirección de propagación. Por lo tanto la
ecuación [2.26] representa una onda plana que se propaga en la dirección u.
En el caso de una onda plana armónica propagándose en la dirección u,
escribimos
ξ ( r,
t)
= ξ0senk(
u.r − vt)
[2.27]
y definiendo un vector k=k.u denominado vector propagación ó vector de onda
ξ r , t)
= ξ sen(
k.r − ωt)
= ξ sen(
k x + k y + k z − ω ) [2.28]
(
0 0 x y z
t
El vector propagación k tiene por módulo k = 2π λ
y apunta en el sentido de la
propagación. Sus componentes satisfacen la relación
k
2
x
2
2 2 ω
+ k
y
+ kz
=
[2.29]
2
v
Cuando la propagación tiene lugar en un espacio tridimensional, la ecuación
diferencial de onda se convierte en
2
2 2 2
∂ ξ 2⎛
∂ ξ ∂ ξ ∂ ξ ⎞ 2 2
= v
= ∇ ξ
2
⎜ + +
2 2 2
⎟ v
∂t
⎝ ∂x
∂y
∂z
⎠
[2.30]
Las ondas planas [2.27] ó [2.28], aunque contienen las tres coordenadas x, y, z,
son en realidad monodimensionales ya que la propagación es según una dirección
particular, y la situación física es la misma en todos los planos perpendiculares a esa
dirección. En la naturaleza hay sin embargo otras clases de ondas que se propagan
en varias direcciones siendo las más interesantes las ondas cilíndricas y las ondas
esféricas, figura 2.10.
2.6.1 Ondas esféricas. Cuando la perturbación originada en un punto se
propaga con la misma velocidad en todas la direcciones del espacio, medio isótropo,
las ondas resultantes son esféricas. Los frentes de onda, definidos como el lugar
geométrico de los puntos del espacio que para el mismo tiempo presentan igual fase,
son esferas concéntricas respecto al punto donde se originó la perturbación, figura
2.10. Según nos alejamos del origen de la onda, el área del frente de ondas aumenta
con el cuadrado del radio. Este hecho sugiere, dada la necesaria conservación de la
energía y la dependencia de ésta con el cuadrado de la amplitud, que la amplitud de la
onda debe disminuir con la distancia r al origen. Utilizando coordenadas esféricas para
expresar la ecuación diferencial de ondas [2.30] y su solución, y asumiendo una
simetría esférica, se demuestra que una onda esférica viene dada por la expresión.
2-10

2. Movimiento Ondulatorio
1
ξ ( r,
t)
= f ( r − vt)
[2.31]
r
En el caso de que la velocidad de propagación no sea la misma en todas las
direcciones hablaremos de un medio anisótropo.
2.6.2 Ondas cilíndricas. En este caso los frentes de onda son cilindros
coaxiales paralelos a una línea dada, que podemos situar en el eje Z y por tanto
perpendiculares al plano XY, figura 2.10. Un ejemplo de estas ondas sería la
producida por una serie de fuentes distribuidas uniformemente a lo largo de un eje, ó
las ondas de presión generadas en el aire por un cuerda larga. De nuevo
consideraciones energéticas nos permiten intuir que la amplitud de la onda debe
disminuir al aumentar la distancia ρ al eje. La solución exacta a la ecuación diferencial
de ondas en coordenadas cilídricas asumiendo simetría cilíndrica tiene la forma de las
funciones de Bessel. Si consideramos grandes distancias ρ respecto al eje del cilindro,
la ecuación de una onda armónica cilíndrica puede aproximarse por la expresión
ξ
0
ξ ( ρ,
t)
= sen(
kρ
− ωt)
[2.32]
ρ
Un ejemplo particular de las ondas cilíndricas serían las ondas circulares que
se dan cuando la onda se propaga sobre una superficie, como por ejemplo una
membrana ó la superficie libre de un líquido.
Figura 2.10. a) Ondas cilíndricas donde los frentes de onda son cilindros con eje Z y donde, para
grandes distancia respecto al eje, la amplitud de la onda disminuye con la raiz de la distancia al mismo.
b) Ondas esféricas donde los frentes de ondas son esferas con centro en el origen de la perturbación y
la amplitud de la onda disminuye con la distancia al origen.
2-11

2. Movimiento Ondulatorio
2.7 Superposición de ondas
La forma resultante del encuentro de dos ondas en el espacio puede
determinarse como la suma de las perturbaciones producidas por cada onda
separadamente. Este principio de superposición es una propiedad del movimiento
ondulatorio que expresa lo siguiente: cuando dos ó más ondas se combinan, la onda
resultante es la suma algebráica de las ondas individuales. Este fenómeno recibe el
nombre genérico de interferencia y resulta de la linealidad de la ecuación diferencial
de ondas; si ξ 1 y ξ 2 son soluciones de la ecuación de onda, la combinación lineal
ξ 3 =C 1 ξ 1 +C 2 ξ 2 , siendo C 1 y C 2 constantes arbitrarias, también es solución.
Consideremos el caso de la interferencia de dos ondas armónicas planas de
igual amplitud y frecuencia. Sean las ondas armónicas
ξ
ξ
1
2
= ξ sen(
kx−
ωt)
0
= ξ sen(
kx−
ωt
+ δ )
0
[2.33]
donde δ es la constante de fase de la 2º onda.
Por tanto, las ondas 1 y 2 difieren en fase δ y, dado el principio de
superposición previamente expuesto, la onda resultante es la suma
ξ + ξ = ξ sen kx−
ωt)
+ ξ sen(
kx −ωt
+ )
[2.34]
1 2 0
(
0
δ
que utilizando identidades trigonométricas queda
1
1
ξ
1
+ ξ2
= ( 2ξ
0
cos δ ) sen ( kx−
ωt
+ δ )
[2.35]
2
2
La interferencia de las dos ondas da lugar a otra onda armónica, con igual
frecuencia ω y número de ondas k, y amplitud dependiente de la diferencia de fase
1
entre ondas según la expresión 2ξ
0
cos δ . Bastará por tanto analizar cual es la
2
diferencia de fase entre las dos ondas para poder determinar completamente la onda
resultante.
Cuando δ=2πn, figura 2.11.a, las dos ondas están en fase, la amplitud de la
2πn
onda resultante es máxima e igual 2ξ 0 , dado que nos queda cos = cos nπ
= 1, y se
2
dice que tenemos una interferencia constructiva.
2-12

2. Movimiento Ondulatorio
Si δ=(2n+1)π, figura 2.11.b, las dos ondas están en contrafase, la amplitud de la
(2n + 1) π
onda resultante es cero, cos = 0, y tenemos una interferencia destructiva.
2
(a)
Figura 2.11. (a) Interferencia constructiva, diferencia de fase δ=2πn, y (b) destructiva, diferencia de fase
δ=(2n+1)π, de dos ondas armónicas de igual frecuencia y amplitud
(b)
Una causa corriente que origina
diferencias de fase entre dos ondas es
la diferencia de longitudes de los
trayectos que deben recorrer desde su
fuente hasta el punto donde se produce
la interferencia. Supongamos dos
fuentes que están emitiendo ondas
armónicas de igual frecuencia y longitud
de onda y que están oscilando en fase,
tal y como se esquematiza en la figura
2.12. Sus ondas esféricas vendrán
dadas por
ξ = ξ
ξ
1
2
= ξ
01
02
sen(
kr
1
sen(
kr
2
−ωt)
− ωt)
[2.36]
donde r 1 y r 2 son las distancias desde
cualquier punto a las fuentes puntuales
S 1 y S 2 . La diferencia de fase para estas
dos funciones de onda es
Figura 2.12. Fuentes 1 y 2 emitiendo ondas
armónicas en fase y de igual frecuencia e
interfiriendo en el punto P de forma constructiva en
(a) y destructiva en (b). La diferencia de fase entre
las ondas 1 y 2 será función de la diferencia de
camino recorrido
2π
δ = kr1 − kr2
= ∆r
[2.37]
λ
Si la diferencia de camino
recorrido es igual a un número entero
2-13

2. Movimiento Ondulatorio
de longitudes de onda, la interferencia será
constructiva. Si la diferencia de camino es
un número impar de semilongitudes de
onda, la interferencia será destructiva. Pero
r 1 -r 2 =cte define una superficie hiperbólica de
revolución cuyos focos son S 1 y S 2 de tal
forma que cuando r 1 -r 2 =nλ tendremos
interferencia constructiva y hablaremos de
superficies ó líneas ventrales, tal y como se
muestra en la figura 2.13; si r 1 -r 2 =(2n+1)λ/2,
tendremos interferencia destructiva y
hablaremos de superficies ó líneas nodales.
Figura 2.13. Líneas nodales y ventrales debido
a la interferencia de dos fuentes idénticas
Hasta ahora hemos analizado el caso
de fuentes de ondas que están en fase ó
tienen una diferencia de fase constante. En
este caso se dice que las fuentes son
coherentes. En caso de que las fuentes de
onda tengan una diferencia de fase no
constante a lo largo del tiempo se dice que
las fuentes son incoherentes y no se
observa un patrón de interferencia definido.
2.8 Ondas estacionarias
Cuando las ondas están confinadas en el espacio, como las ondas en una
cuerda de piano o las ondas sonoras de un tubo de organo, se producen reflexiones
en ambos extremos y, por consiguiente, existen ondas que se mueven en las dos
sentidos y que se combinan según el principio de superposición. Para una cuerda ó
tubo determinado, existen ciertas frecuencias para las cuales la superposición da un
esquema vibratorio estacionario denominado onda estacionaria. Este tipo de ondas
tienen aplicaciones importantes en campos tan dispares como los instrumentos de
música ó la teoría cuántica.
2-14
Figura 2.14. Reflexión de una onda transversal en una cuerda con un extremo fijo

2. Movimiento Ondulatorio
Consideremos el caso de una cuerda con un extremo fijo tal y como se
esquematiza en la figura 2.14. Una onda transversal incidente moviéndose hacia la
izquierda y de ecuación ξ1 = ξ0sen ( ωt
+ kx)
se reflejará en el extremo O originando una
´
nueva onda que se propaga hacia la derecha y de ecuación ξ = ξ0sen(
ωt
− kx)
. El
desplazamiento en cualquier punto de la cuerda es el resultado de la interferencia ó
superposición de estas dos ondas
´
ξ = ξ0sen(
ωt
+ kx)
+ ξ0sen(
ωt
− kx)
[2.38]
En el punto fijo O x=0 de modo que
´
ξ
( x= 0)
= ( ξ0
+ ξ0)
senwt = 0 ∀ t
[2.39]
pero O es fijo en todo instante. Esto implica que ξ 0´= -ξ 0 , es decir la onda experimenta
un cambio de fase de π cuando se refleja en el extremo fijo, fenómeno que
analizaremos más profundamente en el siguiente apartado. La ecuación [2.38] se
transforma entonces en
[ sen(
ωt
+ kx)
− sen(
t − )]
ξ = ξ0 ω kx
[2.40]
que utilizando identidades geométricas se convierte en
ξ
= ξ senkxcosωt
[2.41]
2 0
Las expresiones ωt±kx no aparecen más y la ecuación [2.41] no representa una
onda viajera sino un movimiento armónico simple cuya amplitud varía de punto a
punto denominándose este tipo de onda como onda estacionaria. La amplitud viene
dada por la ecuación
A = 2ξ senkx 0
[2.42]
que se hace cero para
kx = nπ
ó
x
1
= nλ
2
[2.43]
Estos puntos se denominan nodos. Los nodos sucesivos estan separados por
una distancia λ
2 .
2-15

2. Movimiento Ondulatorio
Estudiemos ahora el caso de una cuerda de longitud L fija por ambos extremos,
figura 2.15. La segunda condición de contorno qua aparece es que x=L sea un nodo.
Figura 2.15. Ondas estacionarias en una cuerda fija por ambos extremos
Utilizando la ecuación [2.43] llegamos a la condición
2L
λ =
[2.44]
n
Esta segunda condición limita automáticamente las longitudes de onda de las
ondas que pueden propagarse en esta cuerda a los valores dados por [2.44] y a su
vez también están limitadas las frecuencias de oscilación a los valores
ω n T
f n
= = = nf
2π
2L
µ
1
[2.45]
donde
f
1
=
2L
T
1
=
µ
v
2L
[2.46]
2-16

2. Movimiento Ondulatorio
es la denominada frecuencia fundamental. De este modo las posibles frecuencias de
oscilación, llamadas armónicos, son todos los múltiplos de la fundamental. Podemos
decir que las frecuencias y las longitudes de onda están cuantizadas. La figura 2.15
indica la distribución de amplitud para los tres primeros modos de vibración. Los
puntos de máxima amplitud son los antinodos y la separación entre nodo y antinodo
es λ
4
.
Una característica importante de la ecuación de ondas estacionarias [2.41] es
que las variables x y t están separadas. Es decir, tenemos una amplitud de vibración
máxima variable a lo largo de la cuerda y fija para cada punto, propiedad fundamental
de las ondas estacionarias. Por tanto una formulación más general de una onda
armónica estacionaria vendría dada por la ecuación
ξ ( x,
t)
= f ( x)
senωt
[2.47]
donde f(x) es la amplitud de onda en un punto x. Pero dado que ξ(x,t) es una onda,
deberá cumplir la ecuación diferencial de ondas [2.9]. Introduciendo [2.47] en [2.9]
encontramos que f(x) debe cumplir la ecuación diferencial
2
d f
2
dx
2
+ k f
= 0
[2.48]
que tiene por solución general
f ( x)
= Asenkx + B cos kx
[2.49]
donde A y B son constantes arbitrarias. Por consiguiente la ecuación de ondas
general de una onda armónica estacionaria viene dada por la ecuación
ξ ( x , t)
= ( Asenkx + B cos kx)
senwt
[2.50]
Las constantes de la ecuación [2.50] se determinan por las condiciones de
contorno. Ilustremos esto con el caso de la cuerda con extremos fijo con condiciones
de contorno ξ(0)=ξ(L)=0
es decir
ξ ( 0, t)
= Bsenwt = 0
implica que B=0
ξ ( L,
t)
= AsenkLsenwt
= 0 implica que kL=nπ
λ = 2L n
donde n es un entero, de conformidad con [2.44].
2-17

2. Movimiento Ondulatorio
2.9 Reflexión y refracción de ondas
Cuando una onda incide sobre una superficie límite ó de separación de dos
regiones en las que la velocidad de la onda es diferente, parte de la onda se refleja y
parte se transmite dando lugar al fenómeno de la reflexión y de la refracción.
Supongamos que la onda incidente está descrita por la ecuación
ξ
i
= ξ sen(
k i
r − ω )
[2.51]
0i
t
Las ondas reflejada y refractada, transmitida, serán
ξ
ξ
r´
r
= ξ
= ξ
0r´
0r
sen(
k
sen(
k
r
r´
r − ωt)
r − ωt)
[2.52]
donde hemos usado la misma frecuencia angular de la onda incidente para la
reflejada y la transmitida porque es un hecho experimental que la frecuencia del
movimiento ondulatorio no cambia en la reflexión ó refracción. La propiedad física
adscrita a ξ, desplazamiento, presión, campo eléctrico ó magnético, es tal que su valor
en la superficie de separación de dos medios debe ser el mismo cualquiera sea el
lado en que calculemos. Ahora bien, en el medio 1 tenemos la onda incidente y
reflejada que produce la perturbación resultante ξ I +ξ r´ y en el medio 2 tenemos solo la
onda refractada ξ r . Entonces en la superficie de separación
ξ + ξ ´
= ξ
[2.53]
i
r
r
Para que se cumpla está ecuación
en todos los puntos de la superficie de
separación en el mismo t es necesario que
las fases de las tres ondas sean idénticas
k r = k
´
r k r
[2.54]
i r
=
r
Figura 2.16. Reflexión y refracción de una onda
en una superficie de separación
para puntos r sobre la superficie de
separación. Escogemos los ejes como se
indica en la figura 2.16 de tal forma que la
superficie de separación coincida con en
plano XZ y la dirección de incidencia esté
en el plano XY. Esto implica que el vector r
está en el plano XZ, r = u x
x + u z .
Análogamente y dado que la dirección de
z
2-18

2. Movimiento Ondulatorio
incidencia está en XY,
k = u + u k y como no sabemos en que plano están
i
k x ix y
contenidas la onda transmitida y la reflejadas
r
rx
y
ry
rz
iy
k = + y
r´ uxk r´
x
+ u
ykr´
y
uzkr´
z
k = u k + u k + u k . Sustituyendo estos vectores en [2.54] obtenemos
x
z
kix x = kr´ xx
+ kr´
zz
= krxx
+ krzz
[2.55]
ecuación válida para todos los puntos del plano XZ, por lo tanto
k
k
ix
r´
z
= k
r´
x
= k
rz
= k
= 0
rx
[2.56]
indicando que los vectores k r´ y k r no tienen componente según el eje Z, estando
contenidos en el plano XY al igual que la onda incidente. Encontramos la primera ley
de la reflexión-refracción que nos dice
que la onda incidente, reflejada y
refractada están en el mismo plano.
Siguiendo ahora la figura 2.17,
encontramos que, siendo θ I el ángulo
incidente sobre el plano XZ y θ r´ el
ángulo de la onda reflejada y θ r el
ángulo de la onda refractada
k
k
k
ix
rx
= k senϑ
i
= k senθ
r
= k
r´ x r´
r´
i
r
senθ
[2.57]
Figura 2.17. Leyes de la reflexión-refracción de
ondas en la superficie de separación de dos
medios
Por otro lado sabemos que
k I =k r´=ω/v 1 y k r =ω/v 2 , que junto a [2.56]
nos permite obtener
1
v
1
senθ
i
1 1
= senϑr´
= senθ
r
[2.58]
v v
1
2
De estas relaciones deducimos que el ángulo de incidencia es igual al ángulo
de reflexión θ I =θ r´ y la ley de Snell, el cociente entre los senos del ángulo incidente y
refractado es igual a la razón de velocidades de propagación de la onda en los dos
medios
senθ
senϑ
i
=
r
v
v
1
2
[2.59]
2-19

2. Movimiento Ondulatorio
Ahora que ya conocemos la relación entre los vectores de onda de las ondas
incidente, reflejada y transmitida, nos falta por analizar las amplitudes de las tres
ondas. Dado que se cumple la ecuación [2.54], igualdad de fase entre las tres ondas,
la ecuación [2.53] se reduce a
ξ + =
[2.60]
0i ξ0r
´
ξ0r
que es la relación entre la amplitud de las tres ondas. Para seguir avanzando
necesitamos una condición de contorno
que implique a las amplitudes de onda y
que depende de cada caso en particular.
Centrémonos en el caso de ondas
transversales en dos cuerdas unidas de
Figura 2.18. Ondas transversales en dos
cuerdas de diferent e densidad unidas
diferentes densidades y sometidas a una
tensión T, tal y como se muestra en la
figura 2.18. Sabemos del análisis realizado
en la sección 2.4.1 que la fuerza vertical en la cuerda 1 donde tenemos onda incidente
y reflejada
F
y
∂ξ
= T
∂x
⎛ ∂ξi
= T ⎜
⎝ ∂x
∂ξr´
+
∂x
⎞
⎟
⎠
[2.61]
y usando [2.51] y [2.52], y teniendo en cuenta que la onda reflejada viaja en dirección
contraria a la onda incidente, nos queda
F
[ − ωt
− k x)
+ ξ cos( t k )]
= Tk1 ξ
0i
cos(
1 0r´
ω
1x
[2.62]
y
+
Análogamente, la fuerza vertical en la cuerda 2 es
F
y
∂ξr
= T = −Tk2ξ
0r
cos( ωt
− k2
x)
∂x
[2.63]
Ahora bien, en el punto de unión, x=0, la fuerza vertical debe ser la misma en la
cuerda 1 y en la 2; por tanto, igualando [2.62] y [2.63] en x=0 obtenemos
k1 ( ξ
0i
ξ0r´
) = k2ξ0r
− [2.64]
Esta es la segunda ecuación que deben cumplir las tres amplitudes y que está
impuesta por la naturaleza física de la onda. Resolviendo el sistema de ecuaciones
dado por [2.60] y [2.64] obtenemos la ecuación [2.65] que nos da la amplitud de la
onda transmitida y reflejada en función de la amplitud de la onda incidente.
2-20

2. Movimiento Ondulatorio
ξ
ξ
0r
0r´
=
k
k
=
k
2k
1
1
1
1
+ k
2
− k
+ k
2
2
ξ
0i
ξ
0i
[2.65]
Usando la igualdad k = ω
v
y, dado que la velocidad en una onda transversal
en una cuerda viene dada por v = T
µ
, obtenemos
ξ
ξ
0r
0r´
=
=
µ
2
µ
1
µ
1
1
+
µ
−
+
1
µ
µ
µ
2
2
2
ξ
0i
ξ
0i
[2.66]
Los cocientes
ξ 0 r
ξ
0i
y
ξ
0r´
ξ
0i
reciben respectivamente los nombres de
coeficiente de transmisión T y coeficiente de reflexión R y viene dados por
T =
R =
µ
2
µ
µ
1
1
1
µ
+
−
+
1
µ
µ
µ
2
2
2
[2.67]
Obsérvese como T es siempre positivo, de manera que la amplitud de la onda
transmitida tiene el mismo signo que la amplitud de la onda incidente, ambas ondas
están en fase. En cambio R es positiva ó negativa dependiendo de si µ 1 en mayor ó
menor que µ 2 de modo que la onda reflejada puede estar en fase ó en oposición, con
un desfase π, con la onda incidente. Las dos situaciones se ilustran en la figura 2.19.
Figura 2.19. Reflexión y transmisión de un onda transversal en el punto de unión de dos cuerdas de
diferente densidad
2-21

2. Movimiento Ondulatorio
2.10 Velocidad de fase y velocidad de grupo
La velocidad v = ω
k
para una onda armónica de frecuencia angular ω y
longitud de onda λ se llama velocidad de fase, y nos dice la velocidad con la que se
propagan los puntos de fase constante (kx-ωt). Sin embargo ésta no es
necesariamente la velocidad que observamos cuando analizamos un movimiento
ondulatorio, generalmente detectado por
su intensidad asociada a su amplitud. Si
tenemos una onda continua, por tanto de
longitud infinita, ésta puede constar de una
sola longitud de onda y de una sola
frecuencia. Pero una onda de estas
características no es adecuada para
transmitir una señal, porque una señal
implica algo que empieza en un cierto
Figura 2.20. Pulso transmitiéndo una señal
instante y termina un cierto tiempo más
tarde. Esto es, la onda debe tener una
forma similar a la representada en la figura 2.20. Vimos como una onda de este tipo
se denomina pulso. Por consiguiente, si medimos la velocidad con que la señal se
transmite, nos estamos refiriendo esencialmente a la velocidad con la que viaja este
pulso.
Este pulso, utilizando el análisis de Fourier, se puede considerar como un
conjunto de ondas armónicas, denominado paquete de ondas, de diferentes
longitudes de onda y frecuencias viajando por el medio. Siempre que la velocidad de
las ondas armónicas no dependa de la frecuencia ó de la longitud de onda, medio no
dispersivo, todas las ondas armónicas que componen el pulso viajaran con la misma
velocidad y el pulso mantendrá su forma al desplazarse. Ejemplos de medios no
dispersivos son una cuerda perfectamente flexible, v = T
µ
no dependiente de la
frecuencia, las ondas sonoras en el aire ó las ondas electromagnéticas en el vacío. En
este caso la velocidad de fase coincide con la velocidad del pulso.
Si la velocidad de la onda en un medio depende de la frecuencia y longitud de
onda, medio dispersivo, las componentes armónicas del pulso se moverán con
velocidades diferentes dando lugar a un cambio de forma del pulso al desplazarse.
Ejemplos de medios dispersivos son cuerdas no perfectamente flexibles ú ondas
electromagnéticas en un material, dando lugar al conocido fenómeno de refracción en
prismas. Por tanto debido a la dispersión, la velocidad del centro del pulso, velocidad
de la señal denominada velocidad de grupo, no es la misma que la velocidad de
propagación de cada una de las ondas armónicas que lo componen.
2-22

2. Movimiento Ondulatorio
Consideremos el caso más sencillo de un pulso consistente en la superposición
de dos ondas armónicas de igual amplitud y de frecuencias muy cercanas,
pulsaciones ó batidos. La onda resultante vendrá dada por
ξ ( x,
t)
= ξ
= 2ξ
0
1
+ ξ
⎡1
cos
⎢
( k
⎣2
2
1
= ξ
− k
2
0
sen(
k x − ω t)
+ ξ
) x −
1
1
2
( ω
1
1
− ω
2
0
sen(
k x − ω
2
⎤ ⎡1
) t
⎥
sen
⎦
⎢
( k
⎣2
1
2
+ k
t)
=
2
) x −
1
2
( ω
1
+ ω
2
⎤
) t
⎥
⎦
[2.68]
y utilizando la notación ∆k=k 1 -k 2 y ∆ω=ω 1 -ω 2 , y valores medios, ω y k , la onda queda
1 ⎛ ∆ω
⎞ ⎛ ω ⎞
ξ( x,
t)
= 2ξ
∆k⎜
x − t ⎟senk
⎜ x − t
⎟
0
cos
[2.69]
2 ⎝ ∆k
⎠ ⎝ k ⎠
onda resultante representada en la figura 2.21 para frecuencias y longitudes de onda
muy cercanas.
Figura 2.21. Pulso resultante de la superposición de dos ondas armónicas de igual amplitud y
frecuencias cercanas
El resultado es una onda de frecuencia angular ω y número de onda k pero
1 ⎛ ∆ω
⎞
con una amplitud modulada por el factor 2ξ
0 cos ∆k⎜
x − t⎟ . La velocidad de onda
2 ⎝ ∆k
⎠
resultante, representada en la figura por la línea continua, v = ω es prácticamente la
k
misma que la de las ondas armónicas que componen el pulso y es la velocidad de
fase. La envolvente del pulso, curva discontinua en el pulso, se propaga como una
onda cuyo número de onda es ∆ k
2
y su frecuencia angular es ∆ ω
2
. La velocidad
correspondiente a esta envolvente, que es la velocidad con la que se propaga el
pulso, se puede calcular considerando el factor de modulación
1
cos
2
v
g
⎛ ∆ω
⎞
∆k⎜
x − t ⎟ =
⎝ ∆k
⎠
∆ω
=
∆k
1
cos
2
∆k
( x − v t)
g
[2.70]
2-23

2. Movimiento Ondulatorio
La velocidad v g
= ∆ ω ∆k
se denomina velocidad de grupo, y en el caso más
general es la velocidad con la que se propaga la amplitud y por tanto la intensidad de
la onda que es proporcional al cuadrado de la amplitud. La frecuencia y la longitud de
onda no son parámetros independientes en un medio, sino que dependen uno de otro.
De ahí podemos escribir que
v g
dω
= [2.71]
dk
generalización de la ecuación [2.70]. La velocidad de fase está definida como v f
= ω
k
y sustituyendo en [2.71] obtenemos la relación entre la velocidad de grupo y la
velocidad de fase.
dω
d
vg = = ( kvf
) = v
f
+
dk dk
dv
f
k
dk
[2.72]
De esta ecuación se deduce que si la velocidad de fase no depende del
número de onda, medio no dispersivo, la velocidad de grupo es igual a la velocidad de
fase. En un medio dispersivo, la velocidad de fase es función del número de onda y la
velocidad de fase y de grupo, velocidad de la señal (máximo de la figura 2.21) no
coinciden. Distinguiremos entre dispersión normal, cuando la velocidad de grupo es
menor que la velocidad de fase, y dispersión anómala, cuando la velocidad de grupo
es mayor que la de fase.
2.10.1 Ondas superficiales en un líquido. Un ejemplo típico de un medio
dispersivo son las ondas superficiales en un líquido. La expresión general para la
velocidad de propagación v de las ondas superficiales de longitud de onda λ en un
líquido de profundidad h, densidad ρ y tensión superficial T es
⎛ gλ
2πT
⎞ 2πh
v = ⎜ + ⎟tgh
[2.73]
⎝ 2π
ρλ ⎠ λ
Como se observa la velocidad de fase depende de la longitud de onda con lo
que un pulso, suma de varios movimiento armónicos de diferente longitud de onda, se
propagará, perdiendo gradualmente su forma inicial, con una velocidad dada por la
velocidad de grupo.
2-24

2. Movimiento Ondulatorio
2.11 Paquete de ondas
Un caso de notable interés es cuando el paquete de ondas está formado por la
superposición de un conjunto infinito de ondas planas de amplitud y frecuencia
variables que se propagan en la dirección X. Una de las componentes quedará
representada, usando notación exponencial, por la ecuación
ξ ( x,
t)
= A exp i(
ω t − kx)
[2.74]
k
k
y el paquete de ondas vendrá dado por
k
∞
∫
−∞
ξ ( x , t)
= A(
k)exp
i(
ω(
k)
t − kx)
dk
[2.75]
Centrémonos en un caso de interés práctico en el que k varía en torno a un
valor central k 0 en un intervalo ∆k pequeño donde A(k) tiene un máximo muy acusado
en k 0 y decáe rápidamente al alejarnos de k 0 . Tratemos de analizar como es la
resultante de esta superposición y con que velocidad se desplaza el conjunto.
En caso de un medio no dispersivo, velocidad de fase independiente de k, la
función ω(k) es muy sencilla, ω=v f k. Si el medio es dispersivo, la velocidad de fase
depende de k y la relación entre ω y k será más complicada. No obstante, por ser ∆k
muy pequeño podemos desarrollar la función ω(k) en serie de Taylor en torno a k 0 en
la forma
⎛ dω
⎞
ω ( k)
= ω(
k0
) + ⎜ ⎟ ( k − k0
) + .....
[2.76]
⎝ dk ⎠
k0
y haciendo ω(k 0 )=ω 0 nos queda
⎡⎛
dω
⎞ ⎤
ω t − kx = ω0t
− k0x
+ ( k − k0)
⎢⎜
⎟ t − x⎥
[2.77]
⎢⎣
⎝ dk ⎠k 0
⎥⎦
con lo que [2.75], tomando la integral en el intervalo k 0 ±∆k/2 que es donde tiene
existencia, se escribirá
k 0 +∆k
/ 2
⎡⎛
dω
⎞
∫
−∆
⎥ ⎥ ⎤
ξ ( x,
t)
= exp i(
ω0t
− k
0t)
A(
k)exp
i(
k − k0)
⎢⎜
⎟ t − x dk [2.78]
k / 2
⎢⎣
⎝ ⎠
0 k
dk k 0 ⎦
Para hacernos una idea del resultado es necesario conocer A(k) para resolver
la integral. Supongamos que A(k)= A 0 es constante, es decir, la amplitud de todas la
2-25

2. Movimiento Ondulatorio
ondas que constituyen el paquete tienen la misma amplitud. Por otro lado, como para
t=0, x=0 todas están en fase, el grupo tendrá la estructura que se muestra en la figura
2.22 y la superposición dará un máximo de gran amplitud en el origen que decae
rápidamente al apartarnos del mismo. Veamos este hecho matemáticamente
realizando la integral en [2.78] con A(k)=A 0 y quedándonos con el coseno del
argumento
⎡∆k
⎛ dω
⎞ ⎤
sen⎢
( ⎜ ⎟ t − x)
⎥
⎢ 2 dk
0
( x,
t)
2A
⎣ ⎝ ⎠k
⎥
ξ =
⎦
0
exp i(
ω0t
− k0x)
[2.79]
⎛ dω
⎞
⎜ ⎟ t − x
⎝ dk ⎠
k
0
Figura 2.22. Superposición de ondas de
amplitud constante y en fase en el origen
Como se ve este paquete de ondas
da lugar a una onda monocromática,
exp[i(ω 0 t-k 0 x)], de frecuencia ω 0 y número
de onda k 0 , y de amplitud modulada. Este
factor de modulación tiene un máximo
acusado de amplitud de valor A 0 ∆k para
⎛ dω
⎞
x = ⎜ ⎟ t disminuyendo rápidamente
⎝ dk ⎠
k 0
hasta extinguirse al alejarnos de este
máximo. El paquete de ondas se reduce, a
diferencia de lo que ocurría cuando
únicamente superponíamos dos ondas de
parecida frecuencia, figura 2.21, a un único
pulso mostrado en la figura 2.23, que se
propaga con la velocidad de grupo
⎛ dω
⎞
vg
= ⎜ ⎟ .
⎝ dk ⎠
k 0
Este análisis resulta muy útil a la
hora de tratar matemáticamente el envío de
información mediante pulsos discontinuos
en el tiempo.
Figura 2.23. Pulso resultante de la
superposición de las ondas
2-26

2. Movimiento Ondulatorio
Problemas
1. La función de onda de una onda armónica que se mueve sobre una cuerda es
y(x,t)=0,3sen(2,2x-3,5t) en unidades del SI. Determinar la dirección del
movimiento, velocidad, longitud de onda, frecuencia y periodo de esta onda. ¿Cuál
es el desplazamiento y velocidad máximos de cualquier segmento de la cuerda
2. Demostrar explicitamente que la función y(x,t)=Asen(kx-ωt) satisface la ecuación
diferencial del movimiento ondulatorio.
3. Ondas de longitud de onda 35 cm y amplitud 1,2 cm se mueven a lo largo de una
cuerda de 15 m que tiene una masa de 80 g y está sometida a una tensión de 12
N. Determinar la velocidad y frecuencia angular de las ondas. Calcular la energía
total media de las ondas en la cuerda.
4. Una cuerda de 1,5 m de longitud posee una densidad lineal de 0,03 kg/m y está
sometida a una tensión de 500 N. Si oscila en su modo fundamental con una
amplitud máxima de 6 cm, ¿cuál es su energía
5. Una fuente oscila con una amplitud de 0,3 m y una frecuencia de 10 Hz unida la
extremo de una cuerda de densidad lineal 0,08 kg/m. Si la longitud de onda de las
ondas que genera es de 1 m, ¿cuánto tiempo ha de estar funcionando para
transmitir una energía 100.000 J.
6. Una cuerda de 3 m de longitud cuelga del techo libremente. Demostrar que la
velocidad de las ondas transversales depende de la distancia y desde el extremo
inferior. Si se genera un pulso de onda en el extremo inferior, ¿cuánto tardará en
subir al techo, reflejarse y regresar al punto inferior de la cuerda
7. Una onda plana tiene la forma f(x,y,t)= Acos(k x x+k y y-ωt). ¿Cómo son los frentes de
onda en este caso Demostrar que la dirección en la que se mueve la onda forma
un ángulo θ= arct(k y /k x ) con el eje x y que la velocidad de propagación de la onda
es v= ω/(k 2 x+k 2 y) 1/2
8. Demostrar que una onda esférica ξ=f(r,t), su valor en un tiempo t depende
únicamente de la distancia al origen r, no puede tener la forma ξ=f(r-vt). Nota:
comprobar que no cumple la ecuación de ondas teniendo en cuenta que el
operador laplaciano en coordenadas esféricas cuando solo depende de r toma la
2
2 2 ∂ξ
∂ ξ
forma ∇ ξ = + . Comprobar que la onda esférica debe tener la forma
2
r ∂r
∂r
1
ξ ( r,
t)
= f ( r − vt)
r
9. Dos focos de ondas emiten en fase. En un punto a 5 m de un foco y 5,17 m del
otro, la amplitud procedente de cada foco por separado es A 0 . Hallar la amplitud de
la onda resultante si la frecuencia de las ondas es 500 Hz, 1000 Hz y 2000 Hz.
(Utilizar como velocidad de las ondas v=340 m/s).
10. Un punto M se encuentra situado en la misma recta y entre dos focos S 1 y S 2 que
emiten ondas sinusoidales transversales del mismo periodo y de igual amplitud.
2-27

2. Movimiento Ondulatorio
Suponiendo que ambos focos emiten con una diferencia de fase nula, hallar la
ecuación del movimiento resultante en el punto M.
11. Dos movimientos sinusoidales con longitud de onda λ=600 nm se desplazan en la
misma dirección pero en sentido contrario. Calcular las abcisas correspondientes a
los planos nodales y ventrales de la onda estacionaria resultante si el desfase es
de 60º.
12. Sean dos fuentes de onda armónicas situadas en el eje x, de igual frecuencia y
amplitud y con una diferencia de fase δ proporcional al tiempo, δ=Ct siendo C una
constante. Escribir las funciones de onda en un punto P del eje x situado a una
distancia x 1 de una de las fuentes y x 1 +∆x de la otra. Hallar la función de onda
resultante. Calcular la intensidad y el valor medio de la misma en el punto P para
∆x=0 y ∆x=λ/2.
13. Una cuerda de 5 m de longitud que está fija solo por un extremo está vibrando en
su quinto armónico con una frecuencia de 400 Hz. ¿Cuál es su longitud de onda,
vector de onda y frecuencia angular Escribir la función de onda correspondiente a
esta onda estacionaria.
14. Una cuerda se estira entre dos soportes fijos distantes 0,7 m entre si y se ajusta la
tensión hasta que la frecuencia fundamental de la cuerda es de 440 Hz ¿Cuál es la
velocidad de las ondas transversales en la cuerda
15. Una cuerda de 3 m de longitud y densidad másica 0,0025 kg/m está sujeta por
ambos extremos. Una de sus frecuencias de resonancia es 252 Hz. La siguiente
frecuencia de resonancia es 336 Hz. ¿Qué armónico corresponde a los 252 Hz
Determinar la frecuencia fundamental y la tensión de la cuerda.
16. Las funciones de onda para dos ondas de igual amplitud, pero que se propagan en
sentidos opuestos, vienen dadas por y 1 = y 0 sen(kx-ωt) e y 2 = y 0 sen(kx+ωt).
Demostrar que la suma de estas dos ondas es una onda estacionaria.
17. Una onda estacionaria sobre una cuerda fija por sus dos extremos viene dada por
y(x,t)=0,024sen(52,3x)cos(480t) en unidades del SI. Determinar la velocidad de las
ondas sobre la cuerda y la distancia entre los nodos.
18. Dos cables de densidades másicas lineales distintas se sueldan uno a
continuación del otro y después se estiran bajo una tensión F. La velocidad de una
onda en el primer alambre es doble que en el segundo y la onda reflejada tiene la
mitad de la amplitud de la onda transmitida. Si la amplitud de la onda incidente es
A, ¿cuál es la amplitud de la onda reflejada y transmitida
19. Hallar, para grandes profundidades, la velocidad de fase y la velocidad de grupo
para ondas superficiales en un líquido
2-28