4 Kinematika Složených Pohybů Mechanismy

48
4 -Kinematika složených pohybů
4. Kinematika složených pohybů. Mechanismy
V řadě případů nás zajímá nejen pohyb vyšetřovaných bodů a těles vzhledem k nehybnému
pozorovateli (tj. k rámu), ale potřebujeme znát informaci i o relativních pohybech mezi
jednotlivými členy mechanických soustav. V řadě případů jsou pak na základě požadavků
tyto pohyby konstrukčně realizovány.
4.1 Současný pohyb bodu a tělesa
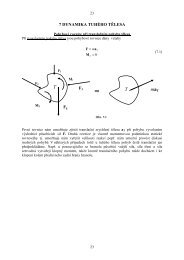
Na obr. 4.1 je kinematický řetězec (soustava těles), který je složen z rámu jedna, kulisy dvě,
tělesa tři. Těleso tři, nazýváme smykadlo a považujeme ho při kinematickém vyšetřování za
bod. Pohyb tělesa 3 vzhledem ke kulise 2 je posuvný a pohyb kulisy vzhledem k rámu je
rotační. Řešíme-li absolutní pohyb tělesa 3 vzhledem k rámu, můžeme jej považovat za
složený ze dvou současných pohybů. Pohybu relativního, kterým rozumíme pohyb tělesa 3
vzhledem ke kulise 2 a pohybu unášivého, kterým rozumíme rotační pohyb kulisy se zdánlivě
spojeným tělesem 3 s kulisou 2. Celá situace je znázorněna na obr. 4.1 a 4.2.
Lze napsat symbolickou rovnici: 31 = 32 + 21 (4.1)
relativní pohyb
unášivý pohyb
4
obr 4.1 obr 4.2
absolutní = relativní + unášivý
Obecně může být vázáno více členů viz obr. 4.3
Zde již nelze určit, který pohyb je relativní a který je unášivý. Můžeme však napsat
a dále
41=43+31 (4.2)
31=32+21 (4.3)
V rovnici (4.2) je pohyb 43 relativní a pohyb 31 unášivý, v rovnici (4.3) je relativní pohyb 32
a unášivý pohyb 21. Je zřejmé, že je možné provést také rozklad
41=42+21 (4.4)
-48-

49
4 -Kinematika složených pohybů
kde je
42=43+32 (4.5)
obr. 4.3
Obecně lze napsat rozklad
mn=mp+pn (4.6)
kde p je člen vložený mezi členy m a n. Z obr. 4.3 a rovnice (4.5) plyne, že za člen vložený
lze považovat i skupinu členů vzájemně vázáných.
Obvykle vyšetřujeme pohyb těles vzhledem na rám. V tomto případě má rovnici (4.6) tvar
m1=mp+p1
(4.7a)
Poznámka: Je-li některý z pohybů přímočarý, pak úhlová rychlost jeho rotace je nulová a
můžeme snadno nalézt vztahy pro hodnoty úhlových rychlostí dalších členů. Např. z obr. 4.3
vyplývá
41= 43+31
31= 32+ 21
(4.7b)
Pohyby 43 a 21 jsou přímočaré, proto tedy platí ω41 = ω
31
a ω31 = ω
32
.
Uvažujme soustavu tří těles včetně rámu. Podobně jako jsme rozkládali obecné
pohyby na translační a rotační složky, můžeme při řešení úlohy rychlostí vyjádřit absolutní
rychlost libovolného bodu tělesa jako součet rychlosti pohybu unášivého a rychlosti pohybu
relativního tj.
v = v + v
B B B
31 32 21
v = v + v
B B B
a r u
B B
B B
kde v31
= v
a
je rychlost absolutní tj. rychlost bodu B vztažená na rám, v32
= v
r
je rychlost
B B
relativní tj. rychlost bodu B tělesa 3 vůči jakoby nehybnému tělesu 2 a v21
= v
u
je rychlost
unášivá tj. bod B chápeme jakoby byl bodem tělesa 2.
Při rozkladu absolutního zrychlení bodu B musíme uvážit to, že jestliže je unášivý pohyb
bodu B je rotační, pak při relativním pohybu dochází ke změně absolutní rychlosti bodu B a to
i v těch případech, kdy oba pohyby jsou rovnoměrné. Např. jestliže se bod pohybuje
rovnoměrně v drážce podél poloměru disku rotujícího s konstantní úhlovou rychlostí, pak jeho
absolutní rychlost (vztažená vzhledem k nepohyblivému pozorovateli se během pohybu mění.
Ke změně rychlosti je však nutná existence nějakého zrychlení. Toto zrychlení se v nazývá
zrychlením Coriolisovým a jeho hodnota je
(4.8)
-49-

50
4 -Kinematika složených pohybů
B
B
c u r
Rovnice pro rozklad zrychlení při složeném pohybu pak má tvar
a = 2( ω x v )
(4.9)
B B B B
aa = au + ar
+ a
C
(4.10a)
Při aplikaci symbolické rovnice (4.1) na konkrétní bod B členu 3 tedy píšeme
( )
B B B B B B B B B
v31 = v32 + v
21
, a31 = a32 + a21 + aC
, aC
= 2 ω21
x v32
(4.10b)
Z rovnice (4.9) je zřejmé, že Coriolisovo zrychlení bude rovno nule v následujících případech.
1) Když ωu = 0, tj. když unášivý pohyb je posuvný, nebo když úhlová rychlost unášivého
pohybu je v daném okamžiku rovna nule.
2) Když v r = 0, tj. když relativní pohyb neexistuje, nebo když v daném okamžiku je relativní
rychlost rovna nule.
3) Když jsou nositelky vektorů ω u a v r rovnoběžné.
Grafická konstrukce Coriolisova zrychlení. Při grafickém vyšetřování složeného pohybu je
potřebné zkonstruovat velikost Coriolisova zrychlení. Vzhledem k tomu, že při rovinném
pohybu je vektor relativní rychlosti kolmý na vektor úhlové rychlosti pohybu unášivého,
můžeme pro velikost
a psát
B
C
a
B
= 2ω
v
(4.11)
B
C u r
Z obr. 4.4 je pak zřejmá možnost konstrukce velikosti zrychlení a C z rychlostí v u a v r
B
B
a C
B
v r
B
v r
Obr. 4.4
Vektor Coriolisova zrychlení pak vynášíme z bodu B, jeho orientaci určíme podle pravidla
pravé ruky z rovnice (4.9).
Poznámka: V případě složených mechanismů můžeme provádět rozklady složených pohybů
ve více variantách tj. můžeme rozkládat m1=mp+p1 nebo m1=mn+n1. Coriolisovo zrychlení
pak bude pochopitelně pro různé varianty rozkladu různé.
Příklad 4.1. Klín mechanismu a kladičkou A se horizontálně pohybuje zrychlením a1
-viz
obr. 4.5. Určete zrychlení zvedátka A. Úhel klínu je ß.
-50-

51
4 -Kinematika složených pohybů
obr. 4.5
Řešení: Zvedátko koná pohyb translační tj. pro určení stačí vyřešit kinematiku středu
kladičky, která je zároveň bodem kladičky (jejího středu). I když to není specifikováno,
zrychlení zvedátka je pochopitelně myšleno vzhledem k rámu. Protože unášivý pohyb bodu A
je určen posuvným přímočarým pohybem klínu tj. a = A 1
a
u
, nevznikne Coriolisovo zrychlení.
Proto zrychlení pro zrychlení středu kladičky A platí
a = a + a
(a)
A A A
a u r
Relativní pohyb bodu A je podél klínu tj. je také přímočarý. Grafické řešení rovnice (a) tedy
můžeme znázornit pomocí vektorového mnohoúhelníku. Viz obr. 4.5. Z obrázku také plyne,
že zrychlení zvedátka vůči rámu je
A
aa
= a tgβ
(b)
4.2 Složený pohyb tělesa
Pohybuje-li se těleso vzhledem na jiné těleso, které se také pohybuje vzhledem na nehybné
těleso (rám), vykonává toto těleso složený pohyb. Je to pohyb relativní a unášivý. Úlohou
kinematiky v tomto případě je určit závislosti mezi charakteristikami relativního, unášivého a
absolutního pohybu. Základní charakteristiky jsou rychlosti a zrychlení bodů, úhlové rychlosti
a úhlová zrychlení těles.
4.2.1 Současné translační pohyby
Nejdříve se budeme zabývat případem, kdy relativní pohyb tělesa je translační a unášivý
pohyb je také translační. Při translačním pohybu mají všechny body tělesa stejnou rychlost a
stejné zrychlení, zrychlení Coriolisovo je nulové. Podle teorie současných pohybů budou mít
tedy všechny body tělesa T3 stejnou rychlost tedy pro jeho libovolný bod B platí
1
v = v + v
B B B
31 32 21
a = a + a
B B B
31 32 21
(4.12)
Absolutní pohyb je tedy opět translační. Úloha kinematiky v tomto případě vede na úlohy
kinematiky bodu.
Poznámka : Při rozkladu složeného pohybu se musí jednat vždy o stejný bod tj. horní index
v rovnicích (4.12) musí být vždy stejný!
4.2.2 Současné rotace okolo dvou rovnoběžných os
Sledujeme případ, kdy relativní pohyb tělesa je rotační s úhlovou rychlostí ω 32 unášivý pohyb
je také rotační s úhlovou rychlostí ω 21 . Viz obr. 4.6.
-51-

52
4 -Kinematika složených pohybů
Podle obr. 4.6 platí
ϕ = ϕ +
ϕ (4.13)
31 32 21
Úhlová rychlost je derivace úhlového pootočení podle času takže platí
ω31 = ω32 + ω
21
(4.14)
Úhlová rychlost absolutní je vyjádřena součtem rychlosti relativní a úhlové rychlosti unášivé .
Podobně vyjádříme úhlové zrychlení . Derivujeme rovnici (4.14) podle času. Obdržíme
Obr. 4.6
α31 = α32 + α
21
(4.15)
Vzhledem k tomu, že vektory obou složek pohybu jsou rovnoběžné, při dvou rotačních
pohybech s rovnoběžnými osy rotací sčítáme úhlové rychlosti a úhlová zrychlení algebraicky
s ohledem na znaménka.
Jak bylo řečeno dříve, mezi základní charakteristiky složeného pohybu patří rychlost
vybraného bodu tělesa. Protože se jedná o současné rotace vyjádříme absolutní rychlost bodu
B pomocí rychlosti relativní a unášivé. Budeme mít
v = v + v = ω x r + ω x r (4.16)
B B B B B
31 32 21 32 21
B
Pro zjištění rychlosti v
31
bychom také mohli použít hodnoty ω
31
, ale v tomto případě bychom
B
museli najít pól absolutního pohybu P 31. . Pak by platilo v31 = ω31xP31B
. Pro hledání pólu
absolutního pohybu používáme tzv. větu o třech pólech:
Okamžitý střed otáčení absolutního pohybu, okamžitý střed otáčení relativního pohybu a
okamžitý střed unášivého pohybu leží na jedné přímce.
Tuto větu používáme i při řešení rovinných mechanismů. Tak např. máme-li určit
absolutní pól pohybu tělesa tři rovinného čtyřkloubového mechanismu postupujeme takto:
Rozložíme pohyby na unášivé a relativní a napíšeme symbolické rovnice, které vyjadřují
složené pohyby. Např. hledáme pól členu 3 u čtyřkloubového mechanismu. Všechny
kinematické dvojice čtyřkloubového mechanismu jsou rotační a tedy se jedná o současné
rotace okolo rovnoběžných os. Platí
-52-

53
4 -Kinematika složených pohybů
31=32+21 (4.17a)
31=34+41 (4.17b)
Pól 31 tedy leží v průsečíku spojnic pólů (32, 21) a (34, 41)- viz obr. 4.8a.
Příklad 4.2. Určete převod planetárního reduktoru, který je tvořen ozubenými koly 1, 2, 3, 3´
o 21 a unašečem 4. Poloměry základních kružnic jsou r 1 , r 2 , r 3 , r 3´, r 4 . Viz obr. 4.11.
Řešení: Orientaci hnací úhlové rychlosti ω
21
položíme souhlasně kolineární s osou x tj. zleva
doprava. Stejnou orientaci budeme předpokládat i pro vypočítávané úhlové rychlosti ω
41
Najdeme body záběru, to je v našem případě body B a C. Pak pro každý z těchto bodů dáme
do rovnosti obvodové rychlosti z obou stran záběru. Pro obvodovou rychlost kola konajícího
složený pohyb provedeme jeho rozklad. Platí:
o 21
o 34
Obr. 4.7
v = v + v (4.18a)
B B B
31 32 21
B
Vzhledem k tomu, že v
32
= 0 (relativní rychlost kol 3 a 2 v bodě B je nulová, jinak by
docházelo k trhání ozubení), pro bod B kola 2 soukolí podle obr. 4.7 pak platí
v = v = v + v (4.18b)
B B B B
21 31 34 41
Pohyb 34 je rotace kola 3 kolem „znehybnělého“ unašeče 4, pro tuto rotaci musíme zavést
další neznámou ω s tím, že orientaci této rotace budeme předpokládat opět zleva doprava.
34
Vektorovou rovnici (4.18b) napíšeme ve složkách do osy z s tím, že znaménka přiřazujeme
podle pravidla pravé ruky, velikosti rychlostí zjistíme vynásobení úhlových rychlostí
B
příslušnými poloměry. Např. bod B leží pod osou o 21 , rychlost v
21
tedy směřuje do nákresny,
B
B
proto jí přisoudíme znaménko (-). Rychlost v
41
směřuje také do nákresny, rychlost v
34
směřuje ven z nákresny (bod B je nad osou o 34 ).
− ω21r2 = ω34r3 − ω41r2
(4.18c)
Podobně pro bod C platí
v = v = v + v (4.19a)
C C C C
11 3´1 3´4 41
-53-

54
4 -Kinematika složených pohybů
Vyjádříme-li obvodové rychlosti pomocí úhlových rychlostí, pak dostáváme
0 r r
= ω3´4 3
− ω41
(4.19b)
Kola 3 a 3´ jsou naklínována na jedné hřídeli, proto musí být ω 3´4 = ω 34 . Řešením rovnic
(4.18c) a (4.19b) obdržíme
−1
⎛ r ⎞
1
ω41 = r2 ⎜ r2 − r3 ⎟ ω21
⎝ r3´
⎠ (4.20)
Poznámka 1: Pokud hodnota některé z vypočítávaných úhlových rychlostí vyjde záporná,
znamená to, že skutečná orientace vektoru této úhlové rychlosti je opačná než jsme
předpokládali tj. musíme smysl jejího vektoru přehodit.
Poznámka 2: Pokud osy rotací jsou různoběžné, pak v případě planetového kuželového
převodu úlohu řešíme podobně tj. provedeme rozklad pohybu v místech odvalování. Úlohu
však můžeme také řešit pomocí vektorové reprezentace pomocí vztahů pro sférický pohyb.
V tomto případě zavedeme počátek kartézské souřadné soustavy v průsečíku os rotací kol,
nadefinujeme v ní potřebné vektory určující kinematiku sférického pohybu (polohové vektory
bodů odvalování, výslednou úhlovou rychlost a výsledné úhlové zrychlení) a dosazujeme do
vztahů pro rychlost a zrychlení bodů tělesa konajícího sférický pohyb.
4.2.3 Současné rotace kolem různoběžných os
Podle obr. 4.8 těleso tři rotuje okolo osy o 32
, která je uložena rotačně v tělese dvě, které rotuje
okolo osy o 21
. Z obr. 4.8 je zřejmé, že bod O zůstává stále v klidu. Jedná se tedy o pohyb
sférický tělesa tři, který lze chápat jako pohyb složený ze dvou pohybů podle rovnice
o 32
o 21
Obr. 4.8b
Obr. 4. 8a
31=32+21 (4.21a)
Hodnotu rychlosti bodu M v tomto případě můžeme najít podle vztahu (3.25) tj.
M
M
v31 = ω31
x r (4.21b)
-54-

55
4 -Kinematika složených pohybů
kde ω31
je celková úhlová rychlost tělesa tři. Tato rychlost je rovna vektorovému součtu
úhlových rychlostí relativního a unášivého pohybu ω
31
= ω
21
+ ω . Vektor úhlového
32
zrychlení získáme derivací vektoru úhlové rychlosti. Protože však vektor úhlové rychlosti
relativního pohybu mění při pohybu svůj směr, v konečném vztahu pro výsledné úhlové
zrychlení α31se kromě úhlových zrychlení α
21
a α
32
je ještě složka α
R
= ω21 x ω
32
, která se
nazývá Résalovo úhlové zrychlení. Výsledné úhlové zrychlení tělesa tři je tedy rovno
Podmínky vzniku Résalova úhlového zrychlení jsou:
a) Existují uvedené rotační pohyby tj. ω21 ≠ 0, ω32
≠ 0 ,
b) Vektory ω21,
ω
32
nejsou rovnoběžné .
α31 = α21 + α32 + α
R
(4.22)
Poznámka: Úhlové zrychlení tělesa konajícího složený pohyb kolem dvou různoběžných os je
tedy různé od nuly i v případě že úhlové frekvence obou složek pohybů jsou veličiny co do
velikosti konstantní!
Příkladem technické realizace pohybu složeného ze dvou vzájemně závisejících rotačních
pohybů s protínajícími se osami rotace jsou kuželové převody. Přitom buď obě kola rotují
(kuželový převod planetový) nebo jedno kolo se ovaluje po druhém kole které je nehybné
(sférický kuželový převod předlohový). Oba případy je přitom vhodné řešit použití vztahů pro
sférický pohyb.
Algoritmus výpočtu rychlosti a zrychlení bodu A tělesa konajícího sférický pohyb se 2
rotačními pohyby:
1) Analyzujeme jednotlivé rotace, pokud jsou závislé, najdeme převodní vztah mezi
hodnotami úhlových rychlostí ω1
a ω
2
a hodnotami úhlových zrychlení α
1
a α
2
.
2) Zvolíme vhodně globální kartézskou souřadnou soustavu (počátek do nehybného
bodu, jedna ze souřadných os shodná s osou základní rotace
3) Ve zvolené souřadné soustavě definujeme vektory ω ,ω , α ,α a polohový vektor
1 2 1 2
4) Nalezneme ω
v
pomocí vektorového sčítání, vektor Résalova zrychlení
vektorového násobení a vektor výsledného zrychlení α = α + α + α
v 1 2 R
A
r
α
R
pomocí
5) Dosadíme do vztahů pro rychlost a zrychlení bodu tělesa konajícího sférický pohyb
-55-

56
4 -Kinematika složených pohybů
Příklad 4.3 Na obr. 4.9 je odvaluje kolo 3 po nehybném kole 1. Úhlová rychlost unašeče 2 je
ω21je konstantní, úhel β a poloměr r 1 jsou známy. Určete výslednou úhlovou rychlost a
výsledné úhlové zrychlení kola 3, rychlost a zrychlení bodu B.
y
x
Obr. 4.9
Řešení: Úlohu nalezení rychlosti a zrychlení bodu B je vhodné provádět pomocí vektorové
reprezentace v kartézském systému se středem v bodě S. Kolo 3 koná složený pohyb který
rozložíme pohyb kola 3 podle schématu
Pro výslednou úhlovou rychlost ω
31
platí
Pro bod A kola 3 (který je pólem rychlosti P 31 ) platí
31=32+21 (a)
ω
31
= ω
21
+ ω (b)
32
v = 0
= v +
v (c)
A A A
31 32 21
z:
r
0
= ω r + ω r ⇒ ω = − ω = − cot gβω
(d)
1
21 1 32 2 32 21 21
r2
Pro vektory úhlových rychlostí tedy můžeme zapsat
ω = ω , 0, 0 , ω = 0, − ω cot g β , 0 , ω = ω , −
ω cot g β , 0
(e)
( ) ( ) ( )
21 21 21 21 31 21 21
Vlastní výpočet přitom můžeme provést 3 způsoby:
a) Použitím vztahů pro sférický pohyb. Sférický pohyb koná kolo 3, neboť bod S jeho
hybného prostoru je trvale v klidu. Nositelka výsledné rychlosti musí procházet středem S a
pólem rychlosti P 31 .
-56-

57
4 -Kinematika složených pohybů
Je-li ω 21 stálá, jsou stálé i hodnoty ostatních úhlových rychlostí. Vektor výsledného úhlového
zrychlení sférického pohybu kola 3 je tedy dán vztahem
2
( 0 0 ω β )
α = α + α + α
R
= α
R
= ω x ω = , , − cot g , (f)
31 32 21 21 32 21
Kinematiku bodu B pak určíme dosazením do vztahů pro sférický pohyb
v = ω x r = 2rω
k (g)
B
B
31 31 1 21
a ω x v α xr r i r (cot g ) j (h)
B B B
2 2
31
=
31 31
+
31
= −
1ω21 +
1ω21 β + 2
B B B B
2 2
b) Nadefinujeme velikosti vektorů v32 = ω32r 2
,v21 = ω21r 1
,a32 = a32n
= r1 ω21 cot g β , aC
= 2ω21r1
.
Směry těchto vektorů zakreslíme do pracovního schématu vektory. Rychlost a zrychlení bodu
B získáme pak můžeme dostat pomocí vztahů pro rozklad složeného pohybu
v B = v B + v B = 2rω k (ch)
31 32 21
1 21
a a a aC r i r (cot g ) j (i)
B B B B
2 2
31
=
32
+
21
+ = −
1ω21 +
1ω21 β + 2
c) Provedeme rozklad obecného prostorového pohybu s tím, že jako referenční bod
S
BS
vezmeme bod S. Zavedeme vektory r = ( r
2
, 0, 0 ), r = ( 2r 2
,r
1
, 0 ) a po dosazení
dostáváme:
v = v + v = v + v = ω xr + ω xr = 2rω
k (j)
B S BS S BS S BS
31 31 31 21 31 21 31 1 21
a = a + a = a + a = ω x v + ω x v + α x r = − r i + r (cot g + ) j (k)
B S BS S BS S BS BS
2 2
31 31 31 21 31 21 21 31 31 31 1ω21 1ω21 β 2
Teoreticky je také možné provést rozklad
4.3 Kinematika mechanismů
v = v + v , a = a + a + a (ch)
BS BS BS BS BS BS BS
31 32 21 31 32 21 C
Mechanismus je zařízení, které slouží k transformaci pohybu nebo přenosu zátěžných
silových účinků. Zařízení je tvořeno soustavou vzájemně pohyblivě spojených těles, z nichž
jedno je vzhledem k ostatním nepohyblivé. Toto nepohyblivé těleso se nazývá rám. Jednotlivá
tělesa nazýváme členy mechanismu. Členy mechanismu jsou spojeny v kinematických
dvojicích.
Kinematická dvojice je spojení těles. Plochy, křivky nebo body členů, které se spolu stýkají a
tvoří tak kinematickou dvojici, jsou prvky této dvojice.
Třída kinematické dvojice. Kinematická dvojice je k-třídy , když odebírá relativnímu pohybu
obou členů jakožto volným tělesům k stupňů volnosti.
Kinematický řetězec vznikne spojením více těles pomocí kinematických dvojic. Může být
jednoduchý i složený, uzavřený i otevřený.
Jednoduchý kinematický řetězec vznikne tak, že každý člen řetězce nemá více než dva
sousední členy, to znamená, že těleso je připojeno k ostatním pouze dvěma kinematickými
dvojicemi.
-57-

58
4 -Kinematika složených pohybů
Složený kinematický řetězec vznikne tak, že některý člen nebo více členů řetězce je připojen
pomocí více než dvou kinematických dvojic.
Uzavřený kinematický řetězec, je řetězec, který vznikne tak, že každý člen řetězce je připojen
nejméně dvěma kinematickými dvojicemi.
Otevřený kinematický řetězec vznikne tak, že obsahuje některé členy které jsou připojeny
pouze jednou kinematickou dvojicí.
4.3.1 Klasifikace mechanismů
1. Všechny mechanismy je možno rozdělit na rovinné a prostorové. U rovinných mechanismů
(i když jsou prostorově konstruovány) všechny body mechanismu se pohybují v rovinách
rovnoběžných, osy rotací jsou rovnoběžné, při grafickém znázorňování jsou tyto osy kolmé na
roviny pohybů. Členy mechanismů nemusí být rovinné útvary tj. desky- např. klikový
mechanismus spalovacího motoru.. U prostorových mechanismů konají jednotlivá tělesa
vzhledem k rámu nebo vůči sobě prostorové pohyby.
2. Nejčastěji se vyskytují mechanismy, které mají jeden stupeň volnosti. Má-li mechanismus
dva stupně volnosti, nazývá se diferenciál.
3. Převodové mechanismy transformují pohyb mezi výstupními a vstupními pohyby.
4. Vodící mechanismy splňují požadavky na to, aby některý člen nebo jeho bod konal určitý
pohyb, např. po přímce (přímovod), nebo aby zaujímal postupně určité polohy.
5. Podle převodu se mechanismy dělí na mechanismy s konstantním převodem (závislost
hnané souřadnice na hnací je lineární) a mechanismy s nekonstantním převodem(závislost
hnaných souřadnic na hnací je nelineární). U prvého typu je pro případ s jedním stupněm
volnosti závislost hnané souřadnice na hnací lineární, u druhého je tato funkce nelineární.
Závislost souřadnice hnaného členu ψ na hnací souřadnici φ nazýváme zdvihovou závislostí
Její derivace se nazývá převod
a další derivací dostaneme tzv. derivaci převodu
ψ = λ( ϕ )
(4.23a)
dλ
µ = (4.23b)
dϕ
2
µ d λ
d
ν = 2
dλ
= dϕ
(4.23c)
Členy, kterými se mechanismus pohání jsou hnací, ostatní jsou hnané. Pohybem
hnacích členů je jednoznačně určen pohyb celého mechanismu. Souřadnice hnacích členů tj.
úhly pootočení hnacích klik, odlehlosti posouvajících se členů apod. se nazývají souřadnice
mechanismu. Ty z hnacích členů, které konají předepsaný pohyb (pro nějž byl mechanismus
konstruován) nazýváme výstupní, ostatní hnané členy se označují jaké přenosové. Při
kinematickém řešení nevycházíme z podrobných výrobních výkresů ale vytváříme
kinematická schémata (modely-viz obr. 4.10). Tyto modely zachycují geometrické uspořádání
(včetně rozměrů) spojených členů pomocí kinematických dvojic. Podle charakteru unášivého
pohybu je i ustálené názvosloví pro členy mechanismu (viz obr. 4.11).
-58-

59
4 -Kinematika složených pohybů
Obr. 4.10
Obr. 4.11
Úkolem kinematického řešení mechanismů je vyšetřit pohyby výstupních členů,
z bodů pak pohyby těžišť, kloubů apod. Při kinematickém řešení rozlišujeme dvě úlohy. Jsou
to analýza a syntéza mechanismů.
A) Analýza mechanismů spočívá v určení polohy, rychlosti a zrychlení resp. úhlové rychlosti a
úhlového zrychlení vybraných bodů resp. těles daného mechanismu v závislosti na hnací
souřadnici.
B) Syntéza mechanismů je inverzní úloha analýzy. Úkolem syntézy mechanismů je navrhovat
typy a geometrii jednotlivých členů mechanismu podle určitých požadavků. Tyto požadavky
se mohou týkat jak kinematiky jeho členů a bodů tak i charakteru přenášených sil (např. aby
nedocházelo k prudkým změnám v hodnotách zrychlení). Hlavním odvětvím syntézy
mechanismů je kinematická syntéza rovinných kloubových a vačkových mechanismů, v níž
jde o určení rozměrů mechanismu, jehož kinematické schéma bylo již zvoleno, aby určitý
jeho člen nebo bod konal předepsaný pohyb. Vačkové mechanismy přitom mohou realizovat
požadovaný pohyb přesně, kloubové mechanismy jen přibližně. Úloha na syntézu
mechanismu je mnohem obtížnější než úloha typu A. Vede na řešení transcendentních rovnic,
které obvykle řešíme numericky na počítačích.
-59-

60
4 -Kinematika složených pohybů
Základní úloha kinematického řešení mechanismů je úloha polohy. Znamená to určit hnané
souřadnice. Od této úlohy odvozujeme řešení rychlostí a zrychlení u požadovaných bodů nebo
těles mechanismu. Před vlastním řešení úloh bychom měli zkontrolovat, zda se skutečně jedná
o mechanismus tj. zda počet stupňů volnosti n je kladný. Hodnota n je přitom dána tzv.
Grueblerovým vztahem
n=(N-1) i v -∑ nkk
, (4.24)
kde N je počet členů soustavy včetně rámu, i v je počet stupňů volnosti jednoho volného tělesa
(i v =3 pro rovinu, i v =6 pro prostor), n k je počet členů k-té třídy, člen k-té třídy odebírá k stupňů
volnosti. V kolika nezávislých směrech (posuvů i rotací) je zabráněno vazbou v pohybu, tolik
stupňů volnosti tato vazba odebírá. Jinými slovy: Počet stupňů volnosti dvojice je roven počtu
nezávislých posuvů a rotací, jež mohou dva členy mezi sebou vzájemně vykonávat. Kolik má
mechanismus stupňů volnosti, pak u tolika členů tedy musí být zadána jejich kinematika. Máli
mechanismus 2 0 V, pak se nazývá diferenciál. Ve statice bývá zaváděna vazba vetknutí.
Z kinematického hlediska je však jednodušší považovat vedení za součást rámu. Pak např. pro
klikový mechanismus na obr. 4.12a uvažujeme počet těles včetně rámu N=4. Je zde jedna
posuvná kinematická dvojice a tři rotační, všechny jsou 2. třídy. Dosazením do vztahu (4.24)
obdržíme n=3(5-1)-2(1+3)=1 0 V.
V některých případech se však mohou v soustavě vyskytovat tělesa, bez kterých je
zachována funkční závislost vstupu a výstupu (např. těleso 3 v soustavě na obr. 4.12b nebo
tělesa 3 a 4 na obr. 4.12c ). Tato vložená tělesa zde jsou z důvodu zpevnění popř. z důvodu
vyvážení při rotaci. Tyto tělesa pak nazýváme kinematicky pasivní a abychom dostali
správnou hodnotu počtu stupňů volnosti podle vztahu (4.24) je vhodné je při kinematickém
rozboru ze soustavy vyjmout. Podobná situace je v tom případě, jestliže u původně
nepohyblivé soustavy je taková výjimková konfigurace vazeb, že nejsou omezeny všechny
složky pohybu (viz možnost horizontálního pohybu u soustavy obr. 4.12d). Při diskusi počtu
stupňů volnosti by také měl být uvážen charakter silového zatížení mechanismu. Jestliže se
některé pohyby vzhledem k charakteru silového zatížení nerealizují (např. u kladkostroje na
obr. 4.12e - volná kladka 2 se nepohybuje do strany, břemeno 4 se nepohybuje do strany a
nenatáčí se), pak stupně volnosti příslušející těmto nerealizovaným pohybů bychom měli při
kinematickém rozboru studovaného mechanismu odečíst. U kladkostroje na obr. 4.12e máme
tedy jednu rotační vazbu, tři obecné (spoje lanem), ale 3 pohyby odečteme, protože se
nerealizují. Pro tento mechanismus počet stupňů volnosti n=3(4-1)-1.2-3.1-3=1 0 V.
Obr. 4.12a Obr. 4.12b
Obr. 4.12d Obr. 4.12e
Obr. 4.12c
-60-

61
4 -Kinematika složených pohybů
4.3.2 Mechanismy s ozubenými koly
Typickým příkladem mechanismů s konstantními převody jsou mechanismy s ozubenými
koly. Při uvolnění v místech záběru ozubených kol je jen jeden neznámý parametr reakce tj.
velikost reakční síly, proto styk ozubením představuje obecnou kinematickou dvojici. Přitom
rozeznáváme předlohové ozubené převody, kdy osy všech kol jsou spojeny s pevným rámem,
jakož i planetové mechanismy, kdy některé členy vykonávají složené rotační pohyby tj. jejich
osy vzhledem k rámu obíhají. Při úloze nalezení úhlových rychlostí hnaných kol, jestliže jsou
dány úhlové rychlosti kol hnacích vycházíme z toho, že absolutní obvodové rychlosti
dotykových bodů ozubených kol musí být stejné. Vzhledem k tomu, že v případě planetových
převodovek se jedná o pohyby složené, provádíme přitom příslušné rozklady na rychlosti
unášivé a relativní (viz kap. 4.2.2 a 4.2.3).
V případě, že osy otáčení jsou rovnoběžné, pak úloha se řeší jako rovinná. V případě
1 0 V je jedno ze záběrových kol hnací, ostatní jsou hnána. Z rovnosti obvodových rychlostí
v místě dotyku nám potom vychází u předlohových převodů vztah mezi úhlovými rychlostmi
ω1 r2
ω = ± r
2 1
(4.25a)
kde při vnějším záběru (obr. 4.13a) jsou vektory úhlových rychlostí orientovány opačně
(znaménko je –) a při vnitřním záběru (obr. 4.13b) jsou úhlové rychlosti obou kol orientovány
stejně (znaménko je +). Počet zubů kol je úměrný poloměrům takže v případě vnějšího záběru
více kol platí obecně vztah
ω
( )
kde k je počet obecných kinematických dvojic (bodů záběru kol).
Poměr p
1
se nazývá převod.
r
z
1
1 k n n
ω = − n
r
= 1
z
(4.25b)
1
ω
n
n= (4.25c)
ω1
Obr. 4.13 a Obr. 4.13b Obr. 4.13c
-61-

62
4 -Kinematika složených pohybů
4.3.3 Rovinné mechanismy
Rovinné mechanismy jsou mechanismy, jejichž jednotlivé členy se pohybují v rovinách
navzájem rovnoběžných. Jsou tvořeny kinematickými řetězci, v nichž se vyskytují
kinematické dvojice rotační, posuvné, valivé a obecné (viz Statika).
I když s rozvojem počítačů se stále více úloh mechaniky řeší na počítačích, grafické
řešení mechanismů má své nezastupitelné místo. Rychlosti libovolných bodů jednotlivých
členů mechanismu pak zjišťujeme následnými způsoby:
1- řešíme graficky sčítání rychlostí, řešíme plány rychlostí resp. zrychlení pomocí základního
rozkladu pro významné body. Aplikujeme věty, tuhosti úsečky, pootočených rychlostech a
podobnosti obrazců,
2- od jednoho členu k druhému přecházíme přes společné body tj.
klouby. V kloubech také provádíme rozklad složeného pohybu,
3- zjišťujeme póly rychlostí a aplikujeme věty o zorných úhlech. Póly
rychlostí hledáme buď jako průsečík známých normál dvou bodů nebo pomocí věty o třech
úhlech.
V případě že unášivý pohyb je translační výsledné zrychlení hledáme pomocí plánů
zrychlení podobně jako při úloze na rychlosti (tj. pomocí rovnoběžníka-tzv. základní
konstrukce). V případě, že unášivý pohyb je rotační, ke zrychlení pohybu unášivého a
relativního přidáváme i vektor zrychlení Coriolisova (tzv. Coriolisova metoda). Metoda
pólové konstrukce je grafická konstrukce rychlostí a zrychlení, prováděná pro bod v pólu
příslušného relativního pohybu (Coriolisovo zrychlení je v tomto bodě nulové i při rotačním
unášivém pohybu).
Poznámka 1: Každý člen má svůj pól absolutního pohybu tj. hledáme póly P 21 , P 21 …P n1 .
Nelze použít pól zjištěný pro jeden člen k řešení kinematiky bodů jiného členu.
Poznámka 2 Pro jeden člen mechanismu můžeme provádět rozklad pohybů tj. můžeme pro
každý člen také hledat póly podle typu pohybu (absolutní, unášivý, relativní) .
Poznámka 3: Při základním rozkladu obecného rovinného pohybu musí oba body příslušet ke
stejnému členu a musí se jednat o stejný pohyb. Např. při použití rovnice v B 31
= v A BA
31
+ v31
musí oba body A a B patřit ke členu 3.
Řešení grafické zpravidla doprovázíme řešením numerickým Je-li úloha vyřešena
polohy pomocí plánů rychlostí a zrychlení, můžeme řešit kinematiku mechanismu tak, že
vektorové rovnice řešíme početně. Provádíme to tak, že rovnice vektorové rozepíšeme do
souřadnicových os. Přitom je vhodné jako podklad použít hlavně grafické řešení pomocí
základního rozkladu obecného rovinného pohybu popř. rozkladu složeného pohybu. Při řešení
rychlostí zpravidla řešíme trojúhelníky pomocí kosinové popř. sinové věty. Řešení zrychlení
jsou již komplikovanější, zde zpravidla sestavíme dvě rovnice pro dvě neznámé na základě
promítání do os do vhodně zvoleného souřadného systému. Neznámými jsou přitom zpravidla
hodnoty tečných složek zrychlení. Hledat hodnoty rychlostí popř. zrychlení numericky
pomocí poloh pólů je zpravidla obtížné. Při početním řešení také můžeme postupovat tak, že
trigonometrickými metodami řešíme obrazec kinematického mechanismu (trigonometrická
metoda). Metoda je vhodná pro základní tříčlenné a čtyřčlenné mechanismy.
Příklad 4.4. Určete pohyb pístu 4 klikového mechanismu na obr. 4.14. Dále určete polohu,
rychlost a zrychlení ojnice 3 téhož mechanismu. Dány jsou délka kliky r, délka ojnice l a
r
1
konstantní úhlová rychlost kliky ɺ ϕ = ω21
.Pro poměr λ = předpokládejte λ ≤ .
l
4
-62-

63
4 -Kinematika složených pohybů
Obr. 4.14
Řešení: Poloha hnacího členu 2 je dána úhlem φ, poloha členu 4 je dána souřadnicí x a poloha
ojnice je dána úhlem ψ . Z trigonometrie trojúhelníku OAB plyne
r
sinψ
= sinϕ
. (a)
l
Pro souřadnici x pak platí
x = r cosϕ
+ l cosψ
(b)
Po dosazení z (a) do (b) a úpravě obdržíme zdvihovou závislost
Použijeme-li pro sin φ binární rozvoj
1
= ϕ + 1 − λ ϕ
( c )
λ
x r(cos
2 sin
2 )
( ) 1
− sin
Odlehlost smykadla 4 je tedy dána vztahem
a jeho rychlost
1 λ ϕ ≐ 1−
λ sin ϕ
(d)
2
41
2 2 1
2 2 2
λ
= 1− ϕ + ϕ
( e )
2
2
x r( cos sin )
( )
v = xɺ = r sinϕ + λ sinϕ cosϕ ɺ ϕ
(f)
Další derivací podle času po úpravách dostáváme pro zrychlení
-63-

64
4 -Kinematika složených pohybů
a ɺ ϕ r(cosϕ λ cos ϕ )
(g)
2
41
= + 2
Proderivováním vztahu (a) podle času a použitím vztahu (d) dostaneme vztah pro úhlovou
rychlost a úhlové zrychlení ojnice
ω
31
=
λ cosϕ
ɺ ϕ
2 2
1−
λ sin ϕ
(h)
2
λ( λ −1)sinϕ 2 λ cosϕ
31
= +
3 1
2 2 2 2 2 2
α ɺ ϕ ɺɺ ϕ
(ch)
( 1−
λ sin ϕ ) ( 1−
λ sin ϕ )
Převod mezi pístem a ojnicí je tedy dán vztahem
v
λ
= = + (i)
41
p24
r(sinϕ
sin 2ϕ
)
ω21
2
U vektorové metody ve vhodně zvolené souřadné soustavě promítneme mnohoúhelník
(představující kinematické schéma mechanismu) do vhodně zvoleného souřadného systému.
Kinematické schéma je přitom charakterizováno mnohoúhelníkem, jehož vrcholy leží ve
středech kloubů, na osách posuvů, ve významných bodech obecných a valivých
kinematických dvojic. apod. Pro daný mechanismus přitom můžeme vykreslit různé varianty
vektorových mnohoúhelníků (viz obr. 4.14, kde je znázorněnoí schéma pětičleného složeného
vačkového mechanismu a 2 varianty vektorových mnohoúhelníků). Strany mnohoúhelníku
považujeme za vektory l i , úhly které tyto vektory svírají s osou x se odměřují vždy
v kladném smyslu (obr. 4.15).
-64-

65
4 -Kinematika složených pohybů
Obr. 4.14
Obr. 4. 15
Z podmínky uzavřenosti vektorového trojúhelníku vyplývá
l + l + l + ... l = 0 (4.26a)
1 2 3 k
-65-

66
4 -Kinematika složených pohybů
Rozepsáním do složek dostáváme systém skalárních rovnic
k
∑ l
j
cosϕ
j
= 0
(4.26b)
j=
1
k
∑ l
j
sinϕ
j
= 0
(4.26c)
j=
1
To jsou rovnice pro polohu mechanismu. Tyto rovnice kromě souřadnic všech hnacích členů
obsahují vždy právě dvě neznámé polohy hnaných členů. Musí být tedy zadány souřadnice
všech hnacích členů, jako neznámé jsou souřadnice 2 hnaných členů. Vztahy pro polohu
hnaných členů tvoří obecně soustavu transcedentních rovnic, kterou je zpravidla potřeba řešit
numericky na počítači. Rychlosti popř. zrychlení 2 hnaných členů dostaneme derivováním
vztahů (4.26b) a (4.26c) podle času
k
( lɺ
∑ j
cosϕ j
l ɺ
jϕ j
sinϕ
j )
j=
1
k
∑( l
j
sinϕ j
l ɺ
jϕ j
cosϕ
j )
j=
1
− = 0
+ = 0
(4.26d)
k
2
(
ɺɺ l
j
cosϕ j
lɺ ∑
ɺ
jϕ j
sinϕ j
l ɺ
jϕ j
cosϕ j
l ɺɺ
jϕ j
sinϕ
j )
j=
1
k
2
(
ɺɺ l
j
sinϕ j
lɺ ∑
ɺ
jϕ j
cosϕ j
l ɺ
jϕ j
sinϕ j
l ɺɺ
jϕ j
cosϕ
j )
j=
1
− 2 − − = 0
+ 2 − + = 0
(4.26e)
Tyto vztahy jsou již lineární.
Poznámka: Máme-li vyšetřovat kinematiku mechanismu tvořeného otevřeným řetězcem,
musíme vytvořit tolik uzavřených systémů rovnic kolik je větví.
4.3.4 Mechanismy s vačkami
Vačka je těleso s obecným obrysem, které se stýká se sousedním tělesem obecnou nebo
valivou kinematickou dvojicí. Zpravidla jsou vačky uloženy k rámu rotační kinematickou
dvojicí a umožňují rotaci o plný úhel 2π. Vačkové mechanismy umožňují transformaci
pohybů- např. rotační pohyb na kývavý (obr.4.12a), rotační na posuvný (obr.4.12b), posuvný
na posuvný (obr.4.12c), a posuvný na kývavý (obr.4.12d). Z důvodu snížení amortizace
kontaktu mezi vačkou a zvedákem (popř. vahadlem) bývají mezi členy vkládány kladečky
(viz obr. 4.12e). V tomto případě můžeme z hlediska kinematiky příslušný mechanismus
nahradit mechanismem bez kladečky s tím, že místo skutečného obrysu vačky k s používáme
tzv. teoretický obrys vačky k e a v místě středu kladečky umístíme obecnou kinematickou
dvojici- viz obr. 4.11e. Teoretický obrys vačky je tedy určen trajektorií středu kladečky při
jejím relativním pohybu vzhledem k vačce jako myšlenému rámu (poloměry křivosti původní
vačky přitom navýšíme o poloměr kladečky).
Význam mechanismů s vačkami je v tom, že je možné vytvořit profil vačky tak, aby v
bylo dosaženo předepsaných pohybů. Přitom předepisujeme buď zdvihovou závislost (tj.
závislost mezi polohou hnaného a hnacího členu) nebo průběh zrychlení (tj. závislost mezi
zrychlením hnaného členu a polohou hnacího členu). Zrychlením je totiž dán průběh
-66-

67
4 -Kinematika složených pohybů
dynamických sil (má-li zrychlení skokové změny, mění se skokem dynamické síly, vznikají
rázy, vibrace, zvětšuje se hluk a opotřebení). Příkladem může být vačkový hřídel u
spalovacích motorů (sání a výfuk-viz obr. 4.12f). Mechanismy s vačkami můžeme řešit
početně i graficky. Při grafickém řešení postupujeme dvojím způsobem.
a) Řešíme rozkladem složeného pohybu bodu S 2 (viz obr. 4.17a). Přitom využíváme toho, že
trajektorií relativního pohybu středu křivosti S 2 je kružnice kolem středu S 1. V případě, že
v dotykovém bodě je křivost jednoho členu nulová (tj. dotykovým útvarem je hrot) řešení
provádíme přímo rozkladem složeného pohybu v dotykovém bodě. Z důvodu snížení
amortizace vačky v dotykovém bodě bývá styk realizovaný valivou kinematickou dvojicí (tj.
(a) (b) (c) (d)
(e)
(f)
Obr. 4.16
kladečkou odvalující se po obrysu vačky). V tomto případě je možné při kinematickém řešení
kladečku myšleně odstranit a uvažovat dotyk zvedáku (popř. vahadla) s teoretickým obrysem
vačky obecnou kinematickou dvojicí. Teoretický obrys vačky přitom vznikne navýšením
původního obrysu o poloměr kladečky-viz obr. 4.16e). V místě dotyku pak provádíme rozklad
složeného pohybu s tím, že relativní pohyb má střed křivosti dráhy ve středu křivosti
aktuálního teoretického obrysu vačky. Toto řešení je zejména nutné použít pro případy, kdy
obrys vačka má rovné úseky takže při náhradě čtyřkloubem by jeden kloub byl totožný
s úběžným bodem. Při přítomnosti kladečky uvažujeme dotyk v teoretickém obrysu vačky
-67-

68
4 -Kinematika složených pohybů
b) Vytváříme náhradní mechanismy. V tomto případě obecné popř. valivé kinematické
dvojice nahrazujeme v uvažované poloze myšlenými mechanismy s větším počtem členů.
Tyto tzv. náhradní mechanismy obsahují pouze rotační a posuvné kinematické dvojice,
původní obecné kinematické dvojice jsou nahrazeny binárními členy. Podmínkou kinematické
ekvivalence původního a náhradního mechanismu je zachování geometrických charakteristik
příslušného relativního pohybu, u něhož došlo k záměně příslušné kinematické dvojice.
V praxi to znamená, že při relativním pohybu 32 náhradního mechanismu musí zůstat
zachovány dva páry sdružených bodů A, S A a B, S B .
Obr. 4.17
Např. mají-li vačky v dotykovém bodě nenulovou křivost, pak vloženým členem je prut o
délce rovné vzdálenosti obou středů křivosti a náhradním mechanismem je čtyřkloub- viz obr
(4.17b). V případě, že jedna křivost má nekonečný poloměr (tj. jedná se o přímku) je nulová,
vkládáme posuvnou kinematickou dvojici rotující kolem středu křivosti druhého útvaru (obr.
4.18a), v tomto středu S pak provádíme rozklad. V případě, že přímka při relativním pohybu
obaluje hrot A, vkládáme smykadlo 4 uchycené kloubem k prutu 2 (viz (obr. 4.18b), pro bod
A pak provedeme rozklad pohybu. Možnosti nahrazení pro případ, že zvedák je opatřen
kladkou popř. při dotyku přímky s kružnicí jsou na obr. 4.19. Náhradními mechanismy jsou
v těchto případech klikový mechanismus (a), čtyřkloubový mechanismus (b), kulisový
mechanismus (c), a mechanismus eliptického pohybu (d). Je nutno zdůraznit, že náhradní
mechanismy zastupují původní mechanismy zpravidla pouze v uvažované poloze. Náhradní
schéma přitom může být ve více variantách (např. místo náhradního schématu 4.19c by mohlo
být také použito schéma obdobné schématu 4.19a). Grafická řešení mechanizmů a vytváření
náhrad pro vačkové mechanismy jsou podrobně zpracovány ve skriptech [9].
S
A
S
4
A
Obr. 4.18a Obr. 4.18b
-68-

69
4 -Kinematika složených pohybů
Obr. 4.19
Příklad 4.5. Určete rychlost a zrychlení plochého zvedáku podle zdvíhaného kruhovou
vačkou (obr. 4.20). Je zadána poloha vačky φ 21, úhlová rychlost vačky ω 21 je konstantní.
Obr. 4.20
K řešení použijeme náhradní mechanismus Obecnou kinematickou dvojici nahradíme
binárním členem rotace-posuv - na obr. 4.14 vyznačeno čárkovaně. Rychlost bodu S můžeme
rozložit na relativní pohyb 4 : 3 a unášivý pohyb 3 : 1. Platí tedy vektorová rovnice
v = v = v + v (a)
S S S S
21 41 43 31
S
S
U vektoru rychlosti v
21
známe jak směr tak i velikost v21 = rω21
a můžeme vyřešit plán
rychlostí. Unášivý pohyb 3:1 je translační, proto rychlost bodu A je rovna rychlosti bodu S.
Tím je vyřešena rychlost bodu A.
-69-

70
4 -Kinematika složených pohybů
Podobně pro zrychlení bodu S platí vektorová rovnice
a = a = a + a . (b)
S S S S
21 41 43 31
Coriolisovo zrychlení nevznikne, protože unášivý pohyb je translační. Protože unášivý pohyb
je translační, je zrychlení bodu A rovno zrychlení bodu S. Tedy . Tím je vyřešeno zrychlení.
Poznámka1: Řešení pomocí původního mechanismu by bylo nepoměrně složitější-viz [3].
Poznámka 2: Náhrada čtyřkloubem je správná pro případ styku těles pomocí obecné
kinematické dvojice tj. jestliže se dotýkající tělesa po sobě smýkají, nikoliv jestliže se po sobě
odvalují.
Poznámka 3: Získaných znalostí mezi rychlostmi bodů popř. úhlovými rychlostmi může
využít k řešení úlohy rovnováhy soustav mechanismů. Jak vyplývá z principu virtuální práce
(viz stud. opora TM I), musí platit i princip virtuálních výkonností: Je-li soustava těles
v rovnováze, je součet celkové výkonnosti pracovních sil
pracovních momentů
P
M
j
roven nule. Tj. platí:
∑
i
∑
F a výkonnosti působících
P
i
P
P
F v + M ω = 0
(4.27)
i i j j
j
Kontrolní otázky
1) Jak je definovaný sférický pohyb
2) Napište vztahy pro rychlost a zrychlení bodů tělesa konajícího sférický pohyb
3) Jak vypočítáme velikost celkového zrychlení z točivého a středového zrychlení?
4) Co je to rozklad složeného pohybu?
5) Co je to unášivý pohyb bodu?
6) Čemu je rovna rychlost čepu pístu 3 na obr. 4.1, jestliže je zadána rychlost ω 21 a
vzdálenost čepu pístu 3 od stálého středu otáčení O 21 ?
7) Proč vzniká zrychlení Coriolisovo, jak jej graficky konstruujeme při rovinném pohybu ?
8) Proč vzniká vír při vtékání kapaliny do výlevky a proč je orientace tohoto víru opačná na
severní a jižní polokouli?
9) Kdy je mechanismus rovinný
10) Co je principem vektorové metody řešení mechanismu
-70-