307 KB - Universität Bremen

Kanalcodierung I
Dr.-Ing. Volker Kühn, Dr.-Ing. Dirk Wübben
Universität Bremen
Fachbereich 1, ANT
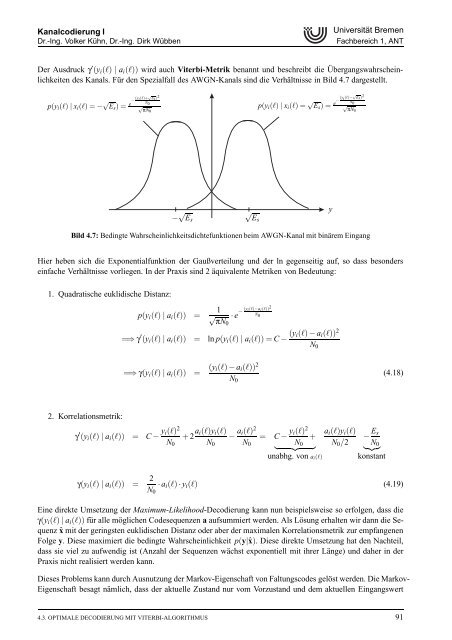
Der Ausdruck γ ′ (yi(ℓ) | ai(ℓ)) wird auch Viterbi-Metrik benannt und beschreibt die Übergangswahrscheinlichkeiten
des Kanals. Für den Spezialfall des AWGN-Kanals sind die Verhältnisse in Bild 4.7 dargestellt.
p(yi(ℓ)|xi(ℓ)=− √ Es)= e−(y i (ℓ)+√Es) 2
N0 √
πN0
− √ Es
√ Es
p(yi(ℓ)|xi(ℓ)= √ Es)= e−(y i (ℓ)−√Es) 2
N0 √
πN0
Bild 4.7: Bedingte Wahrscheinlichkeitsdichtefunktionen beim AWGN-Kanal mit binärem Eingang
Hier heben sich die Exponentialfunktion der Gaußverteilung und der ln gegenseitig auf, so dass besonders
einfache Verhältnisse vorliegen. In der Praxis sind 2 äquivalente Metriken von Bedeutung:
1. Quadratische euklidische Distanz:
2. Korrelationsmetrik:
γ ′ (yi(ℓ)|ai(ℓ)) = C−
γ(yi(ℓ)|ai(ℓ)) = 2
p(yi(ℓ)|ai(ℓ)) =
1
√ · e
πN0
−(y i (ℓ)−ai (ℓ))2
N0 =⇒ γ ′ (yi(ℓ)|ai(ℓ)) = ln p(yi(ℓ)|ai(ℓ))= C−
=⇒ γ(yi(ℓ)|ai(ℓ)) =
N0
yi(ℓ) 2
N0
+ 2 ai(ℓ)yi(ℓ)
N0
(yi(ℓ)−ai(ℓ)) 2
N0
−
ai(ℓ) 2
N0
= C−
y
(yi(ℓ)−ai(ℓ)) 2
yi(ℓ) 2
N0
N0
+
unabhg. von ai(ℓ)
ai(ℓ)yi(ℓ)
N0/2
− Es
N0
konstant
(4.18)
· ai(ℓ)·yi(ℓ) (4.19)
Eine direkte Umsetzung der Maximum-Likelihood-Decodierung kann nun beispielsweise so erfolgen, dass die
γ(yi(ℓ)|ai(ℓ)) für alle möglichen Codesequenzen a aufsummiert werden. Als Lösung erhalten wir dann die Sequenz
ˆx mit der geringsten euklidischen Distanz oder aber der maximalen Korrelationsmetrik zur empfangenen
Folge y. Diese maximiert die bedingte Wahrscheinlichkeit p(y|ˆx). Diese direkte Umsetzung hat den Nachteil,
dass sie viel zu aufwendig ist (Anzahl der Sequenzen wächst exponentiell mit ihrer Länge) und daher in der
Praxis nicht realisiert werden kann.
Dieses Problems kann durch Ausnutzung der Markov-Eigenschaft von Faltungscodes gelöst werden. Die Markov-
Eigenschaft besagt nämlich, dass der aktuelle Zustand nur vom Vorzustand und dem aktuellen Eingangswert
4.3. OPTIMALE DECODIERUNG MIT VITERBI-ALGORITHMUS 91