4 Abbildung durch zentrische Streckung
4 Abbildung durch zentrische Streckung
4 Abbildung durch zentrische Streckung
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
66 4<strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong><br />
Aus der<br />
Geschichte der<br />
Fotografie<br />
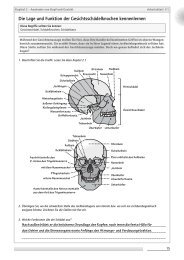
Die <strong>Abbildung</strong> zeigt eine moderne Digitalkamera.<br />
In ihr fängt statt eines Fotofilms ein elektronischer<br />
Sensor das vom Objektiv eingefangene<br />
Licht auf.<br />
Die Entwicklung der fotografischen<br />
Apparate lässt sich auf die Camera obscura<br />
(lat.: dunkle Kammer) zurückführen.<br />
Auf dem abgebildeten Holzschnitt fallen<br />
<strong>durch</strong> ein Loch in einer der Außenwände<br />
Sonnenstrahlen in einen dunklen Raum.<br />
Auf der gegenüberliegenden Wand erscheint<br />
das Bild der Sonne.<br />
Die lateinische Inschrift lautet übersetzt:<br />
Das Verschwinden der Sonne im Jahre 1544,<br />
am 24. Januar, in Louvain. 1<br />
Maler des 17. und 18. Jahrhunderts benutzten<br />
eine tragbare Camera obscura, um<br />
Landschaften naturgetreu nachzeichnen<br />
zu können. Beschreibe anhand der <strong>Abbildung</strong><br />
(Kupferstich 1671) das Bild, das der<br />
Künstler in der Camera obscura auf einer<br />
Leinwand erblickte.<br />
Bereits 1568 empfahl Daniele Barbaro<br />
eine Sammellinse in die Öffnung einer<br />
Camera obscura einzusetzen. Da<strong>durch</strong><br />
wurde das Bild heller und schärfer.<br />
In der Zeichnung siehst du den Strahlenverlauf<br />
in einer Camera obscura, die heute auch<br />
Lochkamera genannt wird.<br />
1<br />
Leuven in Belgien
<strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> 67<br />
1 a) Schneide aus einem 6 cm x 5 cm großen Rechteck<br />
aus Pappe eine Öffnung aus wie z.B. in der<br />
Figur rechts.<br />
Schiebe diese Figur in einen Blendenhalter.<br />
Beleuchte die Figur mit einer punktförmigen<br />
Lichtquelle Z wie in der <strong>Abbildung</strong> unten. Beobachte<br />
das Schattenbild auf dem Schirm. Falls<br />
keine geeigneten Versuchsgeräte zur Verfügung<br />
stehen, kannst du mit dem Tageslichtprojektor das Schattenbild einer ebenen Figur<br />
erzeugen.<br />
b) Finde verschiedene Möglichkeiten die Größe des Schattens der Figur in a) zu verändern.<br />
c) Baue dir mit einem Pappkarton eine Lochkamera wie sie auf Seite 66 unten dargestellt<br />
ist. Erzeuge damit das Bild einer Kerzenflamme.<br />
Hinweis: Das Loch in der Außenwand des Kartons soll ca. einen Durchmesser von<br />
2 mm haben.<br />
d) Beschreibe die Unterschiede der beiden Bilder in a) und in c).<br />
2 In der Zeichenebene kann man ebene Figuren ohne Lichtquelle auf vergrößerte oder verkleinerte<br />
Figuren abbilden.<br />
a) Übertrage die Tabelle in dein Heft und ergänze sie. Was stellst du fest?<br />
C’<br />
C<br />
d<br />
P’<br />
P<br />
α α’<br />
Z A<br />
A’<br />
d’<br />
ZA ZC ZP<br />
d a<br />
in cm in cm in cm in cm<br />
■ ■ ■ ■ ■<br />
ZA ZC ZP d a<br />
in cm in cm in cm in cm<br />
■ ■ ■ ■ ■<br />
b) Finde eine Vorschrift, wie man einen<br />
Punkt P auf einen Punkt P abbilden<br />
kann.<br />
c) Gibt es Fixpunkte bei der nebenstehenden<br />
<strong>Abbildung</strong>?<br />
d) Finde eine Vorschrift, wie man eine<br />
Figur verkleinern könnte.
68 <strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong><br />
A’<br />
α’<br />
P’<br />
Z<br />
C<br />
P<br />
α<br />
A<br />
d<br />
3 In der <strong>Abbildung</strong> ist eine weitere Möglichkeit<br />
dargestellt, wie man die Größe<br />
einer Figur verändern kann.<br />
a) Übertrage die Tabelle in dein Heft und<br />
ergänze sie.<br />
ZA ZC ZP<br />
d a<br />
in cm in cm in cm in cm<br />
■ ■ ■ ■ ■<br />
ZA ZC ZP d a<br />
in cm in cm in cm in cm<br />
■ ■ ■ ■ ■<br />
d’<br />
C’<br />
b) Nenne die Unterschiede zur Aufgabe 2<br />
Seite 67.<br />
c) Finde eine passende <strong>Abbildung</strong>svorschrift.<br />
Zentrische<br />
<strong>Streckung</strong><br />
Punkte und Figuren der Ebene lassen sich <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> auf Bildpunkte<br />
und Bildfiguren der Ebene abbilden. Eine <strong>zentrische</strong> <strong>Streckung</strong> wird festgelegt<br />
<strong>durch</strong> Angabe eines <strong>Streckung</strong>szentrums Z und eines <strong>Streckung</strong>sfaktors k.<br />
Man schreibt: P ƒƒƒƒƒƒƒƒƒ© Z; k P<br />
lies: Der Punkt P wird mit dem Zentrum Z und dem <strong>Streckung</strong>sfaktor k auf den<br />
Punkt P abgebildet.<br />
<strong>Abbildung</strong>svorschrift<br />
<strong>Abbildung</strong>svorschrift der <strong>zentrische</strong>n <strong>Streckung</strong>:<br />
–Urpunkt, Bildpunkt und <strong>Streckung</strong>szentrum liegen auf einer Geraden.<br />
–Jeder Strecke [ZP] wird eine Bildstrecke [ZP] so zugeordnet, dass gilt:<br />
ZP = |k| · ZP (k ≠ 0)<br />
– Das Zentrum Z ist für k ≠ 0 und k ≠ 1 der einzige Fixpunkt.<br />
k > 0 z.B. k = 2,5 k < 0 z.B. k = –2,5<br />
2,5 · ZP<br />
–2,5 · ZP<br />
Z P P’<br />
Die Punkte P und P liegen auf<br />
Die Punkte P und P liegen auf<br />
derselben Seite von Z. verschiedenen Seiten von Z.<br />
Für die Streckenlängen gilt:<br />
ZP = |+ 2,5| · ZP = 2,5 · ZP ZP = |– 2,5| · ZP = 2,5 · ZP<br />
P’<br />
Z<br />
P<br />
Übungen<br />
4 Gib für die <strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> den <strong>Streckung</strong>sfaktor k an.<br />
a) P’ Z P<br />
b)<br />
c) Z P’ P<br />
d)<br />
P<br />
Z P<br />
P’<br />
Z P’
<strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> 69<br />
5 So kann man einen Punkt P <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z und dem positiven<br />
<strong>Streckung</strong>sfaktor k = 1,5 abbilden.<br />
3cm<br />
4,5cm<br />
7<br />
–9<br />
–5<br />
6<br />
Z<br />
Zeichne die Halbgerade [ZP und miss<br />
die Länge ZP.<br />
P<br />
Z P P’<br />
Trage von Z aus die 1,5fache Länge von<br />
ZP auf der Halbgeraden [ZP ab. Du<br />
erhältst den Punkt P.<br />
a) P(–4|1); Z 1 (–1|0); k = 2,5 b) Q(1|0); Z 2 (2|4); k = 0,5<br />
c) R(3|–1); Z 3 (5|2); k = 2 d) S(–2|2); Z 4 (0|3); k = 3<br />
1<br />
e) T(1|5); Z 5 (–1|4); k = 1,5 f) U(–4|4); Z 6 (2|7); k = 3<br />
g) Gib für die Aufgaben a)–f) jeweils denjenigen <strong>Streckung</strong>sfaktor an, mit dem man den<br />
Bildpunkt <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> wieder auf den Urpunkt abbilden kann.<br />
6 So kann man einen Punkt P <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z und dem negativen<br />
<strong>Streckung</strong>sfaktor k = –0,5 abbilden.<br />
3cm<br />
1,5cm<br />
4<br />
–6<br />
–3<br />
5<br />
Z<br />
Zeichne die Halbgerade [PZ und miss<br />
die Länge ZP.<br />
P<br />
Trage von Z aus die 0,5fache Länge von<br />
ZP auf der Halbgeraden [PZ ab. Du<br />
erhältst den Punkt P.<br />
a) P(0|1); Z 1 (–1,5|1); k = –2,5 b) Q(3,5|2); Z 2 (1|0,5); k = –2<br />
c) R(0|2,5); Z 3 (3|3); k = –0,5 d) S(4,5|–1); Z 4 (2,5|–1); k = –3<br />
e) Gib für die Aufgaben a)–d) jeweils den <strong>Streckung</strong>sfaktor an, sodass man den Bildpunkt<br />
<strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> wieder auf den Urpunkt abbilden kann.<br />
7 Zeichne die Figur in dein Heft und bilde sie jeweils mit den angegebenen <strong>Streckung</strong>sfaktoren<br />
von Z aus ab.<br />
a) k 1 = 2; k 2 = –0,5 b) k 1 = –1; k 2 = 2,5 c) k 1 = 0,5; k 2 = –0,8<br />
P’<br />
Z<br />
P<br />
y<br />
y<br />
y<br />
7<br />
D<br />
C<br />
C<br />
Z<br />
D<br />
C<br />
–3<br />
–8<br />
10<br />
1<br />
1<br />
1<br />
Z 1 A B<br />
x<br />
A<br />
1<br />
B<br />
x<br />
A<br />
1<br />
B=Z x<br />
d) Für welche <strong>Streckung</strong>sfaktoren ergibt sich ein verkleinertes Bild?<br />
A k
70 Eigenschaften der <strong>zentrische</strong>n <strong>Streckung</strong><br />
1 Im Folgenden sollen Eigenschaften der <strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> untersucht<br />
werden.<br />
Hauptleiste Konstruieren Abbilden Form&Farbe Messen&Rechnen<br />
ϕ<br />
ϕ<br />
–+<br />
– –<br />
Spurmodus<br />
A’<br />
–3 k = 2,198 5<br />
15,39cm<br />
A<br />
Z<br />
7cm<br />
3,49cm<br />
C<br />
7,68cm<br />
C’<br />
B<br />
P<br />
B’<br />
P’<br />
a) Zeichne mit einem Geometrieprogramm ein Dreieck ABC und die Gerade g = AB.<br />
Binde einen Punkt P an die Gerade g. Bilde den Punkt P an einem Zentrum Z mit einem<br />
beliebigen <strong>Streckung</strong>sfaktor k auf den Punkt P ab.<br />
Bewege mit dem Zugmodus den Punkt P auf der Geraden g und lasse die Spur des Punktes<br />
P aufzeichnen. Was stellst du fest?<br />
b) Bilde das Dreieck ABC <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> ab. Vergleiche den Verlauf von<br />
Urstrecken und Bildstrecken. Was stellst du fest?<br />
c) Miss die Winkelmaße im Ur- und im Bilddreieck. Vergleiche.<br />
d) Miss die Längen ZA, ZA, AB und AB<br />
Verändere mit dem Zugmodus den <strong>Streckung</strong>sfaktor k oder die Form des Dreiecks<br />
ABC. Was stellst du fest?<br />
e) Überprüfe ob es Fixgeraden bei der <strong>Abbildung</strong> <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> gibt.<br />
f) Welche besonderen <strong>Abbildung</strong>en ergeben sich für k = 1 und k = –1?<br />
2<br />
Ich habe im Heft eine Gerade g <strong>durch</strong><br />
<strong>zentrische</strong> <strong>Streckung</strong> auf eine Bildgerade<br />
g abgebildet. Es sieht so aus, als<br />
ob sich g und g schneiden würden.<br />
Dann gibt es bei dir ja zwei<br />
Fixpunkte!<br />
a) Beurteile die Aussage von Claudia und Peter.<br />
Was folgt für denVerlauf von Ur- und Bildgerade bzw. von Ur- und Bildstrecke bei einer<br />
<strong>zentrische</strong>n <strong>Streckung</strong>? Begründe.<br />
b) Begründe, warum bei einer <strong>zentrische</strong>n <strong>Streckung</strong> entsprechende Winkel im Ur- und<br />
Bilddreieck gleiches Maß haben.
Eigenschaften der <strong>zentrische</strong>n <strong>Streckung</strong> 71<br />
3 So kann man zeigen, dass bei einer <strong>zentrische</strong>n <strong>Streckung</strong> eine Strecke [AB] auf eine parallele<br />
Bildstrecke [AB] mit |k|-facher Länge abgebildet wird:<br />
1. Fall: Z AB<br />
Z<br />
H’<br />
H<br />
Z<br />
B<br />
B’<br />
A A’<br />
B’<br />
B<br />
A A’<br />
Für k > 0 gilt:<br />
ZA = k · ZA<br />
ZB = k · ZB<br />
Man zeichnet zusätzlich eine Hilfsstrecke<br />
[ZH] mit [ZH] || [AB] und<br />
ZH = AB.<br />
Die Strecke [ZH] wird ebenfalls <strong>durch</strong><br />
<strong>zentrische</strong> <strong>Streckung</strong> abgebildet.<br />
Damit gilt: ZH = k · ZH<br />
Das Viereck ZABH ist ein Parallelogramm.<br />
Mit ZH = AB und ZH = AB folgt:<br />
AB = k · AB<br />
2. Fall: Z AB<br />
Z A B A’ B’<br />
Für k > 0 gilt:<br />
ZA = k · ZA<br />
ZB = k · ZB<br />
a) Zeige für den 2. Fall im grauen Kasten, dass gilt: AB = k · AB<br />
Setze dazu in deinem Heft für die Platzhalter richtig ein.<br />
AB = ZB – ZA = k · ■ – k · ▼ = k · (■ – ▼) = k · AB<br />
b) Führe ebenso die Beweise für die beiden Fälle für k < 0 <strong>durch</strong>.<br />
4 Begründe: Bei einer <strong>zentrische</strong>n <strong>Streckung</strong><br />
wird ein Kreis k mit dem Radius r<br />
wieder auf einen Kreis k mit dem Radius<br />
r abgebildet. Hinweis: Für alle Punkte P n<br />
auf einem Kreis mit dem Mittelpunkt M<br />
und dem Radius r gilt: P n M = r<br />
P n ’<br />
P n<br />
r’<br />
r<br />
Z M M’<br />
k<br />
k’<br />
Eigenschaften<br />
der <strong>zentrische</strong>n<br />
<strong>Streckung</strong><br />
Eigenschaften der <strong>zentrische</strong>n <strong>Streckung</strong>:<br />
Jedem Punkt P wird eindeutig ein Bildpunkt P zugeordnet.<br />
Sie ist für k ≠ –1 und k ≠ 1 keine Kongruenzabbildung.<br />
Die <strong>zentrische</strong> <strong>Streckung</strong> ist geradentreu, winkeltreu und kreistreu.<br />
Urfigur und Bildfigur haben gleichen Umlaufsinn.<br />
Jede Gerade, die nicht <strong>durch</strong> Z geht, wird auf eine parallele Bildgerade abgebildet.<br />
Jede Gerade <strong>durch</strong> das Zentrum Z ist Fixgerade.<br />
Jede Strecke wird auf eine parallele Bildstrecke mit |k|-facher Länge abgebildet.<br />
Für –1 < k < 1 ist die Bildstrecke kürzer als die Urstrecke.<br />
10<br />
–1<br />
–4<br />
13<br />
5 Bilde das Drachenviereck ABCD und dessen Inkreis <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> am Zentrum<br />
Z mit dem Faktor k ab. Es gilt: A (0|2); B (6|3); C (2|6); D (0|2).<br />
a) Z = D; k = 2 b) Z = B; k = –0,5 c) Z (0|0); k = 0,75
72 Verhältnistreue der <strong>zentrische</strong>n <strong>Streckung</strong><br />
1 Das Dreieck ABC und der Punkt T werden<br />
<strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> abgebildet.<br />
a) Gib den <strong>Streckung</strong>sfaktor k an.<br />
b) Berechne die Streckenlängen AC;<br />
BC; AT; TB.<br />
c) Übertrage die Tabelle in dein Heft und<br />
berechne die angegebenen Streckenverhältnisse.<br />
Was stellst du fest?<br />
AC<br />
BC<br />
AC<br />
BC<br />
AT<br />
TB<br />
AT<br />
TB<br />
■ ■ ■ ■<br />
Z<br />
A’<br />
T’<br />
2cm<br />
A<br />
2cm<br />
T<br />
C’<br />
B’<br />
3cm<br />
4,5cm<br />
4cm<br />
B<br />
C<br />
5,4cm<br />
AC AC AT AT<br />
d) Begründe allgemein: = und =<br />
BC BC TB TB<br />
e) Begründe: Wenn der Punkt M Mittelpunkt der Strecke [BC] ist, dann ist der Punkt M<br />
Mittelpunkt der Strecke [BC].<br />
verhältnistreu<br />
Bei einer <strong>zentrische</strong>n <strong>Streckung</strong> stehen<br />
entsprechende Strecken in der Ur- und<br />
Bildfigur im selben Verhältnis.<br />
Die <strong>zentrische</strong> <strong>Streckung</strong> ist verhältnistreu.<br />
A<br />
A’<br />
T<br />
T’<br />
AT<br />
TB<br />
k · AT<br />
= k · = AT TB TB<br />
Z<br />
B<br />
B’<br />
Übungen<br />
2 So kann man eine Strecke [AB] mit der Länge 4 cm im Verhältnis AT : TB = 2 : 1 teilen.<br />
A<br />
B<br />
A<br />
B<br />
A<br />
T<br />
B<br />
P<br />
2LE<br />
Q<br />
1LE<br />
R<br />
P<br />
Q<br />
R<br />
P<br />
Q<br />
R<br />
Z<br />
Z<br />
Zeichne zu [AB] eine parallele<br />
Hilfsstrecke [PR]<br />
mit 3 LE (= 2 LE + 1 LE).<br />
Der Punkt Q liegt 2 LE von<br />
P entfernt.<br />
Der Schnittpunkt der Halbgeraden<br />
[AP und [BR ergibt<br />
das Zentrum Z.<br />
Die Halbgerade [ZQ<br />
schneidet die Strecke [AB]<br />
im gesuchten Teilpunkt T.<br />
Teile ebenso eine 6 cm lange Strecke [AB] im angegebenen Verhältnis.<br />
a) AT : TB = 3 : 2 b) AT : TB = 7 : 3 c) AT : TB = 2 : 5 d) AT : TB = 3 : 5
Flächeninhalt bei der <strong>zentrische</strong>n <strong>Streckung</strong> 73<br />
1<br />
Wie groß ist<br />
der Flächeninhalt<br />
eines Bilddreiecks<br />
bei einer<br />
<strong>zentrische</strong>n<br />
<strong>Streckung</strong>?<br />
Sicher k-mal so groß<br />
wie der Flächeninhalt<br />
des Urdreiecks.<br />
Ich glaube das zweifache<br />
von k, da die Grundlinie und die<br />
Höhe des Dreiecks zentrisch<br />
gestreckt werden.<br />
7<br />
–7<br />
–5<br />
10<br />
a) Beurteile die zwei Antworten.<br />
b) Zeichne das Dreieck ABC und bilde es <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z<br />
und dem <strong>Streckung</strong>sfaktor k auf das Dreick ABC ab. Es gilt: Z (0|0); A (0|1,5);<br />
B(2|0); C(3|2); k 1 = 3; k 2 = –2<br />
c) Ergänze die Platzhalter in deinem Heft.<br />
A DABC = ■ · A DABC<br />
k<br />
A DABC (FE)<br />
3<br />
■<br />
–2<br />
■<br />
A ■ = k B ■ = 2k C ■ = k 2 A DABC (FE) ■ ■<br />
2 So kann man den Zusammenhang zwischen den Flächeninhalten A und A der Urfigur und<br />
der Bildfigur rechnerisch nachweisen. Ergänze die Platzhalter in deinem Heft.<br />
Es gilt: A DABC = 0,5 · AB · h<br />
A DABC = 0,5 · AB · h<br />
A DABC = 0,5 · |k| · ■ · ■ · ■<br />
A DABC = ■ 2 · 0,5 · AB · h<br />
A DABC = ■ 2 · ■<br />
Z<br />
A<br />
A’<br />
C<br />
h<br />
·<br />
B<br />
·<br />
h’<br />
C’<br />
B’<br />
Flächeninhalt<br />
Bei einer <strong>zentrische</strong>n <strong>Streckung</strong> beträgt<br />
der Flächeninhalt der Bildfigur<br />
das k 2 -fache des Flächeninhalts der<br />
Urfigur.<br />
A = k 2 · A<br />
Z<br />
Übungen<br />
3 Berechne die fehlenden Größen in deinem Heft.<br />
a) b) c) d) e) f) g)<br />
k 3,5 –1,8 ■ –0,2 ■ ■ ■<br />
k 2 ■ ■ ■ ■ 1,69 ■ 121<br />
A 18 cm 2 ■ 12 cm 2 ■ 5 cm 2 50 cm 2 ■<br />
A ■ 16,2 cm 2 1,92 dm 2 2 mm 2 ■ 0,32 dm 2 605 cm 2<br />
9<br />
–6<br />
–3<br />
12<br />
4 Zeichne die Urfigur und die Bildfigur. Berechne die Werte für die Platzhalter in deinem<br />
Heft.<br />
a) DPQR ∂ƒƒƒƒƒƒƒƒƒ© Z; k DPQR; Z (■|■); k = ■; P (■|■); A D = ■ FE; A D = ■ FE<br />
Es gilt: P(–2|–1,5); Q(3|–1,5); R(0|2,5); Q(3|8,5); R(7,5|2,5)<br />
b) Trapez PQRS ∂ƒƒƒƒƒƒƒƒƒ© Z; k Trapez PQRS; k = ■; A Trapez = ■ FE; A Trapez = ■ FE<br />
Es gilt: Z(–5|–2); P(–3|–2); Q(–1|0); R(–1|1); S(–3 | 2); P(0|–2)
74 Vermischte Übungen<br />
1 Ordne die gefundenen Buchstaben richtig an, dann erhältst du ein Lösungswort.<br />
Bei einer <strong>zentrische</strong>n <strong>Streckung</strong> mit dem Zentrum Z und dem wahr falsch<br />
<strong>Streckung</strong>sfaktor k Q (k ≠ 0; k ≠ 1) gilt:<br />
Wenn der Bildpunkt zwischen Z und dem Urpunkt liegt, ist k negativ. Z T<br />
Wenn der Bildpunkt zwischen Z und dem Urpunkt liegt, gilt: 0 < k < 1 R E<br />
Jede Gerade <strong>durch</strong> Z ist eine Fixgerade. U R<br />
Die Bildstrecke hat stets die k-fache Länge der Urbildstrecke. K M<br />
Die Bildfigur hat den k-fachen Flächeninhalt der Urfigur. U Z<br />
Die Bildgerade hat die k-fache Steigung der Urgeraden. S E<br />
1<br />
Mit dem Faktor k kann man P wieder auf P abbilden. N S<br />
2 Bei der <strong>Abbildung</strong> eines Dreiecks ABC <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> ist nur ein Bildpunkt<br />
bekannt. Beschreibe anhand der <strong>Abbildung</strong>en, wie man die weiteren Bildpunkte konstruieren<br />
kann. Schätze ab, wie groß der <strong>Streckung</strong>sfaktor ist.<br />
C’<br />
C’<br />
A’<br />
A’<br />
A’<br />
A<br />
C<br />
A<br />
C<br />
A<br />
C<br />
Z<br />
B<br />
Z<br />
B<br />
Z<br />
B<br />
B’<br />
7<br />
–5 5<br />
3 DABC ∂ Z; k ƒƒƒƒƒƒƒƒƒ© DABC<br />
Ermittle wie in Aufgabe 2 <strong>durch</strong> Konstruktion die Bildfigur. Gib jeweils k an.<br />
a) A(1|2,5); B(2,5|1); C(3|2); B(–2|1); Z(0|1)<br />
b) A(0|1); B(4|1); C(2|3); C(2|6); Z(2|0)<br />
c) A(0|0); B(3|1); C(–0,5|1,5); A(1,5|4,5); Z(1|3)<br />
4 Im Bild wird eine Gerade g <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z (2|1) und<br />
k=2,5 auf die Bildgerade g abgebildet.<br />
a) Gib die Gleichung von g an.<br />
b) Begründe, warum man nur einen Punkt P der Geraden g abbilden muss.<br />
c) Begründe rechnerisch: Der Punkt P hat die Koordinaten (2|3,5).<br />
d) Welcher der folgenden Punkte der Geraden g wäre für die <strong>Abbildung</strong> ebenfalls gut<br />
geeignet? Begründe.<br />
A Q(4|3) B R(–2|0) C S(0|1)<br />
e)<br />
y<br />
g: y = 0,5x + 1; P(2|2) g<br />
g’<br />
Z (2|1); k = 2,5<br />
P(2|2) ∂ƒ ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ© P(2|3,5) g<br />
Es gilt: m = m = 0,5<br />
P’<br />
Q g<br />
Gleichung von g: y= 0,5 (x – x p )+ y p<br />
Mit P (2|3,5) folgt:y = 0,5 (x – 2) + 3,5<br />
P<br />
Ergebnis: g: y = 0,5x + 2,5<br />
Berechne wie im Beispiel die Gleichung<br />
von g mithilfe von Aufgabe d).<br />
R<br />
1<br />
O<br />
S<br />
1<br />
Z<br />
x
Vermischte Übungen 75<br />
6<br />
–2<br />
–4<br />
6<br />
–2<br />
13<br />
–7<br />
–5<br />
4<br />
5<br />
11<br />
5 Die Gerade g wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> auf die Gerade g abgebildet. Zeichne die<br />
Geraden g und g. Bestimme wie in Aufgabe 4, Seite 74, die Gleichung der Geraden g.<br />
a) g mit y = –x + 4; Z(3|4); k = 2 b) g mit y – 2x = 1; Z(3|1); k = –0,5<br />
c) g mit y + 0,5x = 2; Z(0|4); k = 1,5 d) g mit y = 3x – 1; Z(1|0); k = –0,75<br />
L y = –x + 3; y = 3x – 4,5; y = –x + 1; 0,5y = x – 4; 2y = –x + 2; y = 3x – 1,5<br />
6 Das Trapez ABCD wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> auf das Trapez ABCD abgebildet.<br />
Es gilt: A(2|1); B(4|1); C(4|2); D(2|4); B(4|–1); D(1|3,5)<br />
a) Bestimme <strong>durch</strong> Zeichnung das Zentrum Z und die fehlenden Bildpunkte.<br />
b) Bestimme die Gleichung der Geraden BB und DD.<br />
c) Zeige <strong>durch</strong> Rechnung, dass gilt: Z(4|5)<br />
d) Berechne den <strong>Streckung</strong>sfaktor k.<br />
e) Berechne die Flächeninhalte von Ur- und Bildtrapez.<br />
7 Das Dreieck ABC wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z (2|y z ) und dem<br />
<strong>Streckung</strong>sfaktor k auf das Dreieck ABC abgebildet. Die Punkte C und Z liegen auf der<br />
Geraden g mit y = –x + 6. Es gilt: A(2|0); B(6|4); C(3|y); A(2|12)<br />
a) Zeichne das Dreieck ABC und den Punkt A. Berechne den <strong>Streckung</strong>sfaktor k.<br />
b) Zeichne das Bilddreieck ABC. Ermittle die Koordinaten der Bildpunkte B und C.<br />
Begründe deren Werte.<br />
c) Welche Gleichung hat die Gerade g bei der obigen <strong>zentrische</strong>n <strong>Streckung</strong>?<br />
d) Berechne den Flächeninhalt des Dreiecks ABC.<br />
e) Das Dreieck A*B*C* ist Bilddreieck zum Dreieck ABC bei einer <strong>zentrische</strong>n<br />
<strong>Streckung</strong> mit dem Zentrum Z und dem <strong>Streckung</strong>sfaktor k* (k* > 0). Der Flächeninhalt<br />
des Dreiecks A*B*C* beträgt 9 FE. Zeichne das Dreieck A*B*C*.<br />
15<br />
–6 10<br />
4<br />
–4 8<br />
8 Die Punkte B n (x|–0,5x + 8) von Dreiecken AB n C liegen auf der Geraden g.<br />
Es gilt: g: y = –0,5x + 8; A(6|0); C(0|4)<br />
a) Zeichne das Dreieck AB 1 C für x = 4 und berechne seinen Flächeninhalt.<br />
b) Das Dreieck AB 1 C und die Gerade g werden <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit Z (2|0)<br />
und k = 1,5 auf das Dreieck AB 1 C bzw. die Gerade g abgebildet. Zeichne das Dreieck<br />
AB 1 C und die Gerade g. Berechne den Flächeninhalt des Dreiecks AB 1 C.<br />
c) Berechne die Gleichnung der Geraden g. [Ergebnis: g: y = –0,5x + 11,5]<br />
d) Der Punkt B*(x|–0,5x + 11,5) liegt auf der Geraden g. Das Dreieck AB*C hat einen<br />
Flächeninhalt von 26 FE. Berechne die Koordinaten von B*.<br />
9 Eine Deckenlampe L leuchtet einen auf dem Boden liegenden kreisförmigen Spiegel mit<br />
dem Durchmesser AB = 50 cm aus. An der Decke des 2,50 m hohen Raumes entsteht <strong>durch</strong><br />
Reflexion eine helle kreisförmige Fläche.<br />
a) Zeichne einen verkleinerten Schnitt der Lichtbündel.<br />
Es gilt: L (0|2,5); A (3|0); B (3,5|0) L<br />
(x-Achse: 1 cm 1 m;<br />
y-Achse: 1 cm 1 m)<br />
b) Welchen <strong>Streckung</strong>sfaktor könnte man<br />
dem Vorgang zuordnen? Welchen<br />
Flächeninhalt hat der Kreis an der<br />
Decke?<br />
c) Die Raumhöhe beträgt 3,00 m.<br />
d) Die Lampe wird in 1,25 m Höhe angebracht.<br />
A<br />
B
76 Ähnliche Figuren<br />
1 Monika möchte mit einem Grafikprogramm die Größe von Bildern verändern.<br />
a) Beschreibe, wie sie dabei vorgehen kann.<br />
b) Bei welchen Bildern handelt es sich um eine maßstäbliche<br />
Vergrößerung (Verkleinerung), welche Bilder sind<br />
bei der Größenänderung verzerrt worden? Wie kannst<br />
du eine Verzerrung erkennen?<br />
Original A<br />
Bild A1<br />
Bild A2<br />
Bild A3<br />
Original B<br />
D<br />
C<br />
A<br />
B<br />
Bild B1<br />
Bild B2<br />
Bild B3<br />
D’<br />
A’<br />
C’<br />
B’<br />
D’<br />
A’<br />
C’<br />
B’<br />
D’<br />
A’<br />
C’<br />
B’
Ähnliche Figuren 77<br />
2 a) Miss im Original B auf S. 76 die Längen<br />
AB und AD des Rechtecks ABCD.<br />
b) Miss die Längen AB und AD in den<br />
Bildern B1, B2 und B3 auf Seite 76.<br />
Ergänze die Tabelle in deinem Heft.<br />
Was stellst du fest?<br />
c) Welche Bildfigur kann <strong>durch</strong> <strong>zentrische</strong><br />
<strong>Streckung</strong> aus dem Original B<br />
erzeugt werden? Begründe.<br />
B1 B2 B3<br />
AB in cm ■ ■ ■<br />
AD in cm ■ ■ ■<br />
AB<br />
AB<br />
■ ■ ■<br />
AD<br />
AD<br />
■ ■ ■<br />
3<br />
Das große Dreieck ist doch eine<br />
maßstäbliche Vergrößerung des kleinen<br />
Dreiecks. Eigentlich müsste ich dann die<br />
beiden Dreiecke <strong>durch</strong> <strong>zentrische</strong><br />
<strong>Streckung</strong> aufeinander abbilden können.<br />
Es funktioniert aber nicht!<br />
y<br />
R<br />
Q<br />
Drehe doch zuerst das kleine Dreieck<br />
mit 90° um den Punkt A.<br />
C<br />
6<br />
1<br />
A<br />
B<br />
P<br />
–4 6<br />
O<br />
1<br />
x<br />
Übertrage die Zeichnung in dein Heft. Überprüfe die Aussagen von Verena und Rupert.<br />
Gib den <strong>Streckung</strong>sfaktor k (k > 0) an. Ermittle das <strong>Streckung</strong>szentrum Z.<br />
Z; k = –1,5<br />
Fig. F ∂ƒƒƒƒƒƒƒƒƒƒƒƒƒƒ©<br />
Fig. F*∂<br />
s<br />
ƒƒƒƒƒƒƒ©<br />
Fig. F<br />
a<br />
ähnliche<br />
Figuren<br />
Zwei Figuren F und F heißen ähnlich,<br />
wenn man sie <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong><br />
(eventuell noch zusätzlich <strong>durch</strong><br />
eine Kongruenzabbildung) aufeinander<br />
abbilden kann.<br />
Man schreibt: Figur F ˜ Figur F<br />
lies: Figur F ist ähnlich zu Figur F<br />
b<br />
Figur F<br />
α<br />
Z<br />
Figur F*<br />
In ähnlichen Figuren stehen entsprechende<br />
Seitenlängen im gleichen Verhältnis.<br />
a b<br />
= b<br />
Entsprechende Winkel haben gleiches<br />
Maß.<br />
a = a<br />
Figur F’<br />
a<br />
α’<br />
s<br />
a’<br />
b’<br />
Übungen<br />
10<br />
–5<br />
–4<br />
10<br />
4 Überprüfe mithilfe geeigneter <strong>Abbildung</strong>en, ob die Dreiecke ABC und PQR ähnlich sind.<br />
a) A(4,5|1); B(4,5|–1,5); C(6|1); P(0|1); Q(3|1); R(0|6)<br />
b) A(–3|1); B(–1|1); C(–2|4); P(0|0); Q(0|–3); R(4,5|–1,5)<br />
c) A(–4|2); B(–2|2); C(–2,5|4); P(2|2); Q(3|–1,5); R(6|2)
78 Ähnliche Dreiecke<br />
1 a) Sind die beiden Dreiecke ABC und<br />
PQR ähnlich? Was vermutest du?<br />
b) Wie könnte man das Dreieck ABC auf<br />
das Dreieck PQR abbilden?<br />
c) Warum genügt es nur zwei Winkelmaße<br />
zu vergleichen, um zu erkennen,<br />
ob die Dreiecke ähnlich sind?<br />
R<br />
Q<br />
100°<br />
30°<br />
P=A<br />
30° 100°<br />
B<br />
C<br />
2 So kann man zeigen, dass zwei Dreiecke ABC und PQR, die in zwei Winkelmaßen übereinstimmen,<br />
ähnlich sind:<br />
Voraussetzung: b = b; g = g<br />
Daraus folgt: a = a<br />
Durch Kongruenzabbildungen kann man<br />
die Dreiecke so anordnen, dass sie übereinander<br />
liegen.<br />
Mit b = b und g = g (Stufenwinkel)<br />
folgt: [BC] || [QR]<br />
Mit A = P als Zentrum einer <strong>zentrische</strong>n<br />
<strong>Streckung</strong> kann man das Dreieck ABC<br />
auf das Dreieck PQR abbilden.<br />
Deshalb sind die Dreiecke ähnlich.<br />
PQ PR<br />
Für k gilt: k = = = QR<br />
AB AC BC<br />
α=α’<br />
A=P<br />
C<br />
γ<br />
β<br />
B<br />
β’<br />
Q<br />
γ’<br />
R<br />
Ähnlichkeitssatz<br />
für<br />
Dreiecke<br />
Dreiecke sind ähnlich, wenn sie in den<br />
Maßen von zwei Winkeln übereinstimmen.<br />
b = b Ÿ g = g<br />
A<br />
C<br />
γ<br />
β<br />
B<br />
P<br />
R<br />
γ’<br />
β’<br />
Q<br />
Übung<br />
3 Welche Dreiecke sind ähnlich? Begründe.<br />
a) R<br />
b)<br />
C<br />
110°<br />
P<br />
30°<br />
A<br />
30°<br />
A<br />
40°<br />
Q<br />
B<br />
c) d)<br />
B<br />
R<br />
25°<br />
P<br />
75°<br />
B<br />
H<br />
C<br />
g<br />
R<br />
70°<br />
Q<br />
h<br />
G<br />
·<br />
F<br />
S<br />
A<br />
J<br />
·<br />
E<br />
g || h<br />
P<br />
A<br />
B<br />
·<br />
D<br />
C
Ähnliche Dreiecke 79<br />
Weitere Ähnlichkeitssätze für Dreiecke<br />
weitere Ähnlichkeitssätze<br />
für Dreiecke<br />
Das erinnert<br />
mich an die<br />
Kongruenzsätze<br />
Dreiecke sind ähnlich, wenn sie im<br />
C 1<br />
C 2<br />
Verhältnis entsprechender Seitenlängen<br />
übereinstimmen.<br />
a 1<br />
b 1<br />
b 2<br />
a 2<br />
a 1 b<br />
=<br />
1 c<br />
=<br />
1<br />
a 2 b 2 c 2<br />
A 1 c 1 B 1<br />
A 2 c 2 B 2<br />
Dreiecke sind ähnlich, wenn sie im<br />
Verhältnis zweier Seitenlängen und<br />
C 1<br />
C 2<br />
dem Maß des eingeschlossenen Winkels<br />
übereinstimmen.<br />
2<br />
b 1<br />
b<br />
α<br />
b c 1<br />
1<br />
=<br />
1<br />
b 2 c 2<br />
; a 1 = a 2<br />
A 1 c B<br />
α 2<br />
1 1<br />
A 2 c 2 B 2<br />
Dreiecke sind ähnlich, wenn sie im Verhältnis<br />
zweier Seitenlängen und dem<br />
1<br />
C 2<br />
C<br />
Maß des Gegenwinkels der größeren<br />
b 1<br />
b 2<br />
der beiden Seiten übereinstimmen.<br />
β 1<br />
b 1 c<br />
=<br />
1<br />
A<br />
b 2 c 2<br />
; b 1 = b 1 c B<br />
β 2<br />
1 1 2<br />
A 2 c 2 B 2<br />
Übungen<br />
4 a) Nenne die den vier Ähnlichkeitssätzen entsprechenden Kongruenzsätze.<br />
b) Für welche Werte von k sind bei <strong>zentrische</strong>n <strong>Streckung</strong>en Ur- und Bilddreieck zusätzlich<br />
kongruent? Welche <strong>Abbildung</strong> liegt jeweils vor?<br />
5 Welche der abgebildeten Dreiecke sind ähnlich. Begründe (alle Längen in cm).<br />
3,9<br />
1,35 100° 3,125<br />
I<br />
II<br />
III 2,1<br />
·<br />
2,7<br />
2,75<br />
3<br />
VI<br />
53° 45°<br />
45°<br />
IV<br />
V<br />
1,75<br />
3,75<br />
3,25<br />
82°<br />
53°<br />
VIII<br />
1,4<br />
VII<br />
IX<br />
100°<br />
·<br />
3,3 2,5 2,8<br />
2,1<br />
6<br />
–6<br />
–4<br />
7<br />
6 Zeichne die Dreiecke A 1 B 1 C 1 und A 2 B 2 C 2 . Überprüfe sie auf Ähnlichkeit und begründe.<br />
a) a 1 = 6 cm; b 1 = 4 cm; c 1 = 5 cm; a 2 = 25 mm; b 2 = 3 cm; c 2 = 2 cm<br />
b) a 1 = 80°; b 1 = 60°; a 2 = 80°; g 2 = 40°<br />
c) a 1 = 4,5 cm; b 1 = 3 cm; g 1 = 55°; a 2 = 6 cm; b 2 = 4 cm; g 2 = 55°<br />
d) A 1 (1|0); C 1 (1|4); c 1 = 5 LE; a 1 = 60°; A 2 (–1|–1); C 2 (–5,8|–1); c 2 = 6 LE;<br />
a 2 = 60°<br />
e) a 1 = 7 cm; b 1 = 5,6 cm; b 1 = 50°; a 2 = 5 cm; b 2 = 4 cm; a 2 = 55°<br />
f) A 1 (2|1); B 1 (6|1); b 1 = 4 LE; a 1 = 45°; A 2 (–3|–3); B 2 (–1|–3); b 2 = 2 LE;<br />
C 2 g mit y = x
80 Ähnliche Dreiecke<br />
7 So kann man mithilfe der Ähnlichkeit von Dreiecken ein fehlendes Längenmaß<br />
z.B. CD = x cm berechnen:<br />
[AB] und [BC]<br />
liegen je einem<br />
90°-Winkel,<br />
[AC] und [CD]<br />
dem Winkel b<br />
gegenüber.<br />
Die beiden Dreiecke ABC und BCD<br />
sind ähnlich, da sie in zwei Winkelmaßen<br />
übereinstimmen.<br />
ACB = BDC = 90° und b = b<br />
Ordne entsprechende Strecken einander<br />
zu.<br />
[AB] ƒƒƒƒƒƒƒ© [BC]<br />
[AC] ƒƒƒƒƒƒƒ© [CD]<br />
A<br />
8cm<br />
10cm<br />
C<br />
·<br />
xcm<br />
·<br />
D<br />
6cm<br />
β<br />
B<br />
In ähnlichen Dreiecken stehen entsprechende<br />
Strecken im selben Verhältnis.<br />
CD BC<br />
Also gilt: AC = AB<br />
xcm<br />
D<br />
·<br />
Setze die Maßzahlen der gegebenen<br />
x 6<br />
Längen ein: 8 = 10<br />
Ergebnis: CD = 4,8 cm<br />
C<br />
6cm<br />
β<br />
B<br />
Berechne wie im Beispiel die Länge BD.<br />
8 Berechne die unbekannten Streckenlängen (alle Angaben in cm). Runde auf zwei Stellen<br />
nach dem Komma.<br />
a) E b) c)<br />
E<br />
15<br />
5,64<br />
C<br />
C<br />
y<br />
A<br />
x<br />
y<br />
4<br />
2,5<br />
35 25<br />
1,5<br />
x<br />
· α · · β β<br />
·<br />
A 2 B 2,5 D A 40 B x D<br />
E<br />
2,8<br />
B<br />
·<br />
D<br />
C<br />
2,62<br />
9 Die <strong>Abbildung</strong> zeigt einen Ausschnitt der<br />
Anlaufspur einer Schisprungschanze.<br />
Es gilt: AC = 10,5 m; BC = 3,5 m<br />
a) Begründe: g = d = e = 90° – a<br />
b) Begründe: Die Dreiecke ABC und<br />
PQR sind ähnlich.<br />
c) Berechne die Hangabtriebskraft F H ,<br />
wenn der Schispringer eine Gewichtskraft<br />
von F G = 720 N hat.<br />
d) Ändere die Aufgabe für einen Vorgang<br />
in deiner Umgebung geeignet ab.<br />
A<br />
α<br />
P ·<br />
·<br />
R<br />
ε<br />
F H<br />
·<br />
δ<br />
F G<br />
Q<br />
C<br />
γ<br />
·<br />
B<br />
L zu 8 und 9: 3,74; 240; 4,17; 17,14; 3,33; 35,71; 1,60
Vierstreckensätze 81<br />
1 Zwei Geraden, die sich in einem Punkt Z<br />
schneiden, werden von zwei parallelen<br />
Geraden g und h geschnitten.<br />
a) Begründe, dass gilt:<br />
ZA ZB ZA AB<br />
ZC = ZD und ZC = CD<br />
b) Übertrage die Tabelle in dein Heft und<br />
ergänze dort die Platzhalter. Was stellst<br />
du fest?<br />
ZA<br />
AC<br />
ZB<br />
BD<br />
ZC<br />
AC<br />
ZD<br />
BD<br />
■ ■ ■ ■<br />
c) Suche nach ähnlichen Dreiecken. Ergänze die Platzhalter in deinem Heft.<br />
ZA ZR ZB ZR<br />
AC =<br />
■<br />
; BD =<br />
■<br />
ZA ZB<br />
Begründe anschließend: AC = BD<br />
ZC ZD<br />
d) Begründe ferner: AC = BD<br />
e) Formuliere einen Satz zu den Ergebnissen in Aufgabe c) und d).<br />
Z<br />
3,2cm<br />
3,8cm<br />
B<br />
R<br />
2,1cm<br />
A<br />
g<br />
α<br />
D<br />
α’<br />
Q<br />
2,5cm<br />
S<br />
α’’<br />
α = α’ = α’’<br />
P<br />
C<br />
h<br />
Werden zwei sich schneidende Geraden von zwei Parallelen geschnitten, dann gilt:<br />
1. Die Streckenabschnitte auf der einen Geraden verhalten sich wie die entsprechenden<br />
Streckenabschnitte auf der anderen Geraden.<br />
D<br />
B<br />
D<br />
B<br />
C<br />
Z<br />
A<br />
B<br />
Vierstreckensätze<br />
Z A C<br />
ZA<br />
ZC<br />
D<br />
Z A C<br />
ZB<br />
ZA ZB<br />
ZA<br />
= ZD<br />
ZC = ZD<br />
AC =<br />
ZB<br />
BD<br />
2. Die Streckenabschnitte auf den Parallelen verhalten sich wie die (von Z ausgehenden)<br />
zugehörigen Strecken auf einer Geraden.<br />
D<br />
B<br />
Kurz zu lang<br />
wie<br />
kurz zu lang!<br />
B<br />
ZA<br />
ZC<br />
=<br />
AB<br />
CD<br />
C<br />
Z<br />
A<br />
Z A C<br />
D<br />
Weil man immer vier Strecken zueinander ins Verhältnis setzen kann, spricht man<br />
von Vierstreckensätzen 1 .<br />
1<br />
In manchen Büchern spricht man auch von Strahlensätzen.
82 Vierstreckensätze<br />
Übungen<br />
2 Ergänze die Platzhalter in deinem Heft.<br />
ZA ■ ■ ZC ■ ■<br />
a) ZD = = b) = =<br />
■ ■ ZE ■ ■<br />
ZE ■ ■ BE ■ ■<br />
c) FE = = d) AF = =<br />
■ ■<br />
■ ■<br />
FD ■ AD ■<br />
e) DZ = f) DF =<br />
■<br />
■<br />
F<br />
D<br />
E<br />
C<br />
Z<br />
B<br />
A<br />
3 Berechne die Längen der gefärbten Strecken (alle Maße in cm). Es gilt: [AB] || [CD]<br />
Tipp:<br />
Bei Bruchgleichungen<br />
kannst du über<br />
Kreuz multiplizieren!<br />
5<br />
B 2<br />
2,4<br />
A<br />
3,6<br />
Z<br />
D<br />
x<br />
y<br />
C<br />
1. Möglichkeit:<br />
Vierstreckensatz<br />
ZA ZB<br />
AC = BD<br />
Für die Maßzahlen gilt:<br />
3,6 2,4<br />
x = 5<br />
3,6 · 5 = x · 2,4<br />
3,6 · 5<br />
x = 2,4<br />
2. Möglichkeit:<br />
Ähnlichkeitssatz<br />
ZC ZD<br />
ZA = ZB<br />
x + 3,6 2,4 + 5<br />
3,6 = 2,4<br />
(x + 3,6) · 2,4 = 7,4 · 3,6<br />
7,4 · 3,6<br />
x + 3,6 = 2,4<br />
Ergebnis: AC = 7,5 cm<br />
9<br />
a) D<br />
b) C<br />
c)<br />
8<br />
A<br />
y<br />
x<br />
30<br />
D<br />
21<br />
B<br />
24<br />
18<br />
Z<br />
15<br />
B<br />
3,3<br />
Z 3<br />
2<br />
A<br />
5<br />
C<br />
y<br />
D<br />
27<br />
7<br />
B<br />
x<br />
Z<br />
x<br />
A<br />
y<br />
C<br />
4<br />
( I ) D<br />
( II )<br />
1,5<br />
B<br />
x<br />
6<br />
3<br />
C 2<br />
y<br />
y<br />
Z<br />
2,5 5<br />
Z 4 A x C<br />
D<br />
–––– = ––––––; –– = –– –– 5 = –––– x ; –– = –––– 5<br />
2<br />
4+x<br />
4<br />
6+1,5<br />
6<br />
3<br />
y<br />
x<br />
4<br />
2,5<br />
4<br />
y<br />
2,5<br />
A<br />
4<br />
B<br />
Sandra und Marcel haben zu einigen geometrischen Figuren Verhältnisgleichungen aufgestellt.<br />
a) Suche in den Figuren nach ähnlichen Dreiecken.<br />
b) Überprüfe die Ansätze und korrigiere falls nötig. Berechne die Werte für x und y.<br />
1<br />
L zu 3 und 4: 1,60; 1; 2,4; 6,25; 34,2; 5 3 ; 26,25; 17,5; 4,5; 52; 6,3; 5,5
Aufgaben aus der Optik 83<br />
1 Auf einer senkrechten Schiene kann eine<br />
Lampe zu Beleuchtungszwecken verschoben<br />
werden. Von einer 1,70 m hohen<br />
Figur werden Schatten an einer 4 m hohen<br />
Projektionswand erzeugt (siehe <strong>Abbildung</strong>).<br />
Die Lampe hat von der Wand<br />
3,60 m Abstand.<br />
a) Berechne die Höhe h des Schattens,<br />
wenn die Lampe ganz unten an der<br />
Schiene montiert wird und 2,40 m Abstand<br />
von der Figur hat.<br />
b) Berechne die Höhe des Schattenbildes<br />
auf der Projektionswand, wenn die<br />
Figur in Aufgabe a) 60 cm näher an die<br />
Lampe herangerückt wird?<br />
c) Wie weit darf die Figur in Aufgabe a)<br />
an die Lampe herangerückt werden,<br />
damit das Schattenbild gerade noch auf<br />
die Projektionswand passt?<br />
d) Die Lampe befindet sich in 1,50 m<br />
Höhe und hat von der Figur 2,40 m Abstand.<br />
Berechne die Schattenhöhe.<br />
e) Die Lampe soll so verstellt werden,<br />
dass der Schatten um 20 cm höher ist<br />
als in d).<br />
f) Ändere die Aufgabe geeignet ab und<br />
ermittle die Lösung.<br />
P 2<br />
P 1<br />
P 2<br />
P 1<br />
h<br />
Lampenschiene<br />
Projektionswand<br />
Lampenschiene<br />
Projektionswand<br />
h<br />
L 1; 3,40; 2,55; 1,80; 1,53; 1,10; 0,30; 1,8<br />
2 Damit sich eine Person mit der Größe a ganz im Spiegel sieht, müssen die Lichtstrahlen,<br />
die vom Fußpunkt F und vom Scheitelpunkt S auf den Spiegel auftreffen, ins Auge A<br />
reflektiert werden.<br />
Die scheinbaren Bildpunkte F und<br />
S S’<br />
S erhält man geometrisch <strong>durch</strong><br />
A<br />
Q<br />
Achsenspiegelung an der Spiegeloberfläche.<br />
Die minimale Spiegelhöhe<br />
wird <strong>durch</strong> die Streckenlänge<br />
PQ (siehe <strong>Abbildung</strong> rechts)<br />
bestimmt.<br />
a) Zeige <strong>durch</strong> Rechnung, dass gilt:<br />
PQ = 0,5a<br />
b) Reicht eine kleinere Spiegelhöhe,<br />
a<br />
P<br />
wenn man sich weiter vom Spiegel<br />
entfernt? Begründe.<br />
F s s F’<br />
Die Summe der rundum sichtbaren Augenzahlen dreier übereinander stehender<br />
Würfel ist 45. Welche Augenzahl muss die obere Fläche tragen?<br />
?
3 7 8 9 10 20 21 22 23 24 25 26 27 28 29 30 31 32 34 35 36 37<br />
40 41 42<br />
17<br />
11 12 14 15 16<br />
1 2 4 5 6<br />
20 21 2 23 24 25 26 27 28 29 30 31 32 3 34 35 36 37 38 39 40 41 42<br />
1 12 13 14 15 16 17 18 19<br />
1 2 3 4 5 6 7 8 9 10<br />
84 Anwendungen aus der Vermessungskunde<br />
1 Zur Messung kleiner Öffnungen kann<br />
man einen Messkeil verwenden.<br />
a) Bestimme die Größe x cm der Öffnung<br />
in der <strong>Abbildung</strong>.<br />
b) Begründe das Messverfahren mithilfe<br />
eines Vierstreckensatzes oder mithilfe<br />
ähnlicher Dreiecke.<br />
c) Baue dir mit selbst gewählten Abmessungen<br />
einen solchen Messkeil und<br />
probiere ihn aus.<br />
3,4cm<br />
xcm<br />
10cm<br />
1cm<br />
2 Mit einem Försterdreieck kann man die<br />
Höhe von Bäumen oder Gebäuden näherungsweise<br />
bestimmen.<br />
a) Erkläre wie man dabei vorgehen muss.<br />
b) Bestimme die Höhe des Baumes im<br />
Bild.<br />
c) Baue dir ein Försterdreieck und<br />
bestimme damit die Höhe eines Baumes<br />
in deiner Umgebung.<br />
33 38 39 40<br />
3 Förster Unterholz bestimmt mit seinem Meterstab die Baumhöhe. Er klappt ihn auf 42 cm<br />
Länge zusammen und klebt bei der 4,2 cm-Marke ein Streichholz auf. Den Meterstab hält<br />
er mit gestrecktem Arm lotrecht vor sich hin. Anschließend geht er so weit vom Baum<br />
weg, bis sich das obere Ende des Meterstabs mit der Baumspitze und das untere Ende mit<br />
dem Stammfuß deckt. Dann schaut er, wo für den Streichholzkopf der entsprechende Bildpunkt<br />
am Baumstamm ist. Diesen merkt er sich. Nun misst er den zugehörigen Abstand<br />
bis zum Boden. Die gemessene Strecke multipliziert er mit 10. Er behauptet, nun habe er<br />
in etwa die Baumhöhe.<br />
h 1<br />
h 2<br />
s 1<br />
s 2<br />
h 1 *=42cm<br />
13 18 19 20<br />
h 2 *=4,2cm<br />
a) Überprüfe damit, ob das Vorgehen des Försters richtig ist. Ergänze dazu in deinem Heft<br />
die Platzhalter.<br />
h*<br />
h*<br />
1 s s<br />
=<br />
2<br />
;<br />
2<br />
=<br />
2<br />
h 1 ■ h 2 ■<br />
h* Begründe anschließend: h 1 =<br />
1 · h 2<br />
; h 1 = 10 · h 2<br />
h 2<br />
*<br />
b) Ermittle mit dieser Methode die Höhe eines geeigneten Objekts in deiner Umgebung.
Anwendungen aus der Vermessungskunde 85<br />
4 Die Gruppen A, B und C der Klasse 9 a haben versucht, mit drei unterschiedlichen Methoden<br />
die Breite des Inns zu vermessen.<br />
A B C<br />
Inn xm<br />
Inn xm<br />
Inn<br />
xm<br />
33,5m<br />
30m<br />
· 2m<br />
· 2m<br />
3m 25m<br />
14m<br />
14m<br />
· · · 75°<br />
·<br />
35m<br />
16m<br />
a) Beschreibe, wie die einzelnen Gruppen dabei vorgegangen sein könnten. Welche Messgeräte<br />
waren erforderlich? Welche Schwierigkeiten könnten aufgetreten sein?<br />
b) Das Vermessungsamt hat an der Messstelle eine Flussbreite von 125 m ermittelt.<br />
Welche Gruppe hat das beste Messergebnis?<br />
c) Versucht die Breite eines Flusses in eurer Umgebung zu bestimmen.<br />
5 Der griechische Mathematiker Thales<br />
von Milet (ca. 640–550 v.Chr.) soll<br />
ein Verfahren entwickelt haben zur<br />
Messung der Höhe von ägyptischen<br />
Pyramiden. Darüber schreibt Diogenes<br />
Laertius um 200 n. Chr.:<br />
„Thales hat die Höhen der Pyramiden<br />
mittels ihres Schattens gemessen, den<br />
er genau zu dem Zeitpunkt abmaß, wo<br />
unser Schatten und unser Leib die<br />
gleiche Länge haben“.<br />
Dieses beschriebene Verfahren wird<br />
aber angezweifelt. Eher glaubwürdig<br />
ist, dass Thales einen Stab lotrecht so<br />
aufgestellt hat, dass das Ende seines<br />
Schattens mit dem Ende des Schattens<br />
der Pyramide zusammenfiel.<br />
Berechne mit den angegebenen Werten<br />
die Höhe der Cheopspyramide.<br />
A 115 m B 146 m C 165 m<br />
6m<br />
2m<br />
317m<br />
·<br />
h<br />
230m<br />
Ein Ausflugsschiff fährt auf dem Inn eine 3,6 km lange Strecke flussabwärts mit 12 .<br />
km<br />
Auf dem Rückweg flussaufwärts ist es mit 8 h unterwegs.<br />
Wie groß ist die Durchschnittsgeschwindigkeit für die Gesamtstrecke?<br />
km<br />
h
86 Aufgaben aus der Geometrie<br />
1 Berechne die Inhalte der farbig markierten Flächen, auf zwei Stellen nach dem Komma<br />
gerundet (alle Angaben in cm).<br />
a) b)<br />
6<br />
·<br />
3<br />
10<br />
α’<br />
6<br />
3,6<br />
4<br />
α<br />
Z<br />
· ·<br />
3,6<br />
Z<br />
α = α’<br />
6<br />
5<br />
2 Von einer Geraden g ist das blaue Steigungsdreieck gegeben.<br />
a) Welche Länge hat im Steigungsdreieck PQR die Strecke [QR]? Der Punkt R ist in der<br />
<strong>Abbildung</strong> nicht sichtbar.<br />
b) Bestimme die Gleichung der Geraden<br />
g, wenn gilt: P (5|4,5) g<br />
c) Bestimme die Koordinaten der Punkte<br />
P<br />
Q und R.<br />
3 Q<br />
d) Begründe: Das blaue und das grüne<br />
Steigungsdreieck sind ähnlich.<br />
1,5<br />
e) Berechne mithilfe von d) die Länge AB<br />
h<br />
1<br />
und gib anschließend die Steigung m* C · B<br />
der Geraden h an.<br />
–m<br />
f) Wie kannst du die Steigung von h noch<br />
berechnen?<br />
g) Berechne die Gleichung von h.<br />
g<br />
A<br />
3 Der Flächeninhalt A 2 des Trapezes ACDB<br />
beträgt das Achtfache des Flächeninhalts<br />
A 1 des Dreiecks ZAB.<br />
Es gilt: AB = 6 cm; AZ = 15 cm<br />
a) Begründe: Das Dreieck ZAB kann<br />
<strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> auf das<br />
Dreieck ZCD abgebildet werden.<br />
[Teilergebnis: k = 3]<br />
b) Berechne die Längen AC und CD.<br />
Z<br />
D<br />
B<br />
A 2<br />
A 1 · ·<br />
A<br />
C<br />
2 3<br />
L zu 1, 2 und 3: 3 ; 2 ; 30; 3; 18; 4,5; (8|9); (8|5); (8|4,5); –0,6; 28,26<br />
2<br />
y = – 3 x + 5,6; y = 1,5x – 3; y = –3x + 1,5; 12,96; 30; 4,52; 4,67<br />
4 a) Zeichne ein Trapez ABCD mit den Grundseiten [AB] und [CD].<br />
Es gilt: a = 9 cm; c = 6 cm; h = 4 cm; a = 60°<br />
b) Der Punkt T teilt die Strecke [AB] so, dass gilt: AT : TB = 2 : 1.<br />
Zeichne den Punkt T und den Schnittpunkt Z der Diagonalen ein.<br />
c) Die Halbgerade [TZ schneidet die Strecke [CD] im Punkt S.<br />
Zeichne diesen Punkt S. Miss die Längen CS und SD. Was stellst du fest?<br />
d) Begründe ohne Messung, dass gilt: AT : TB = CS : SD = 2 : 1.
Aufgaben aus der Geometrie 87<br />
S 2<br />
5 Gegeben ist das Quadrat ABCD. Zwei parallele Geraden g und h schneiden die Gerade<br />
w= AC in den Punkten S 1 und S 2 .<br />
Es gilt: A (0|0); B (6|0); Q (6|3); g = DQ, h = PR; PQ = 2 LE<br />
a) Ermittle die Gleichungen der Geraden g, h und w.<br />
b) Berechne die Koordinaten der Punkte S 1 und S 2 .<br />
c) Begründe: Die Dreiecke AS 1 R und<br />
CS 2 Q sind ähnlich.<br />
D<br />
C<br />
w<br />
d) Das Dreieck AS 1 R kann <strong>durch</strong> <strong>zentrische</strong><br />
<strong>Streckung</strong> mit dem Zentrum Z<br />
und dem <strong>Streckung</strong>sfaktor k (k < 0) auf<br />
II<br />
das Dreieck CS 2 Q abgebildet werden.<br />
R<br />
Gib den <strong>Streckung</strong>sfaktor k an.<br />
Ermittle <strong>durch</strong> Konstruktion das Zentrum<br />
Z.<br />
e) Berechne die Flächeninhalte der beiden<br />
S 1<br />
Q<br />
g<br />
Dreiecke AS 1 R und CS 2 Q.<br />
I<br />
P<br />
f) Berechne die Flächeninhalte der beiden<br />
Trapeze ABPR und RS 1 S 2 D.<br />
h<br />
6 Der blaue und orange Kreis sind dem<br />
Dreieck ABC einbeschrieben (siehe <strong>Abbildung</strong>).<br />
Die Radien der Kreise betragen<br />
r 1 = 3 cm und r 2 = 5 cm.<br />
a) Berechne die Länge der Strecke [CM 1 ].<br />
[Ergebnis: CM 1 = 12 cm]<br />
b) Zeichne das Dreieck und die Kreise im<br />
Maßstab 1: 2.<br />
c) Die Basis [AB] des Dreiecks ABC ist<br />
12,9 cm lang. Berechne wie viel Prozent<br />
der Dreiecksfläche nicht von<br />
Kreisflächen bedeckt sind. Runde auf<br />
ganze Prozent.<br />
A<br />
A<br />
C<br />
B 2<br />
M 1<br />
·<br />
B 1 r<br />
· 1<br />
r 2<br />
M 2<br />
B<br />
B<br />
Die <strong>Abbildung</strong> zeigt : 64 cm 2 = 65 cm 2<br />
3cm<br />
8cm<br />
8cm<br />
5cm<br />
5cm<br />
5cm<br />
Q<br />
5cm<br />
5cm<br />
3cm<br />
5cm<br />
P<br />
8cm<br />
a) Zeichne das Quadrat auf kariertes Papier und zerschneide es in einzelne Teilflächen.<br />
Lege diese wie in der <strong>Abbildung</strong> rechts. Was stellst du fest?<br />
b) Wo steckt der Fehler? Lies dazu die Länge der Strecke [PQ] im Kästchengitter ab.<br />
Ermittle anschließend die Länge PQ rechnerisch. Vergleiche beide Ergebnisse.
88 Einbeschreibungsaufgaben<br />
1 Dem Dreieck ABC wird ein Rechteck PQRS so einbeschrieben, dass die Seite [PQ] auf<br />
der Strecke [AB], der Punkt R auf [BC] und der Punkt S auf [AC] liegt. Die Seite [PQ]<br />
des Rechtecks ist doppelt so lang wie die Seite [QR]. Es gilt: A(1|1), B(9|1), C(3|6)<br />
So kann man diese Aufgabe <strong>durch</strong> Zeichnung lösen:<br />
A Notiere alle Bedingungen, die in dieser<br />
y<br />
Aufgabe erfüllt werden müssen.<br />
C<br />
6<br />
I [PQ] [AB]<br />
II PQ : QR = 2 : 1<br />
5<br />
III R [BC]<br />
4 S 3 R 3<br />
IV S [AC]<br />
3<br />
B Probiere systematisch, d.h. zeichne 2<br />
S2<br />
S1<br />
Rechtecke P n Q n R n S n , die die Bedingungen<br />
I, II und III erfüllen.<br />
1<br />
P 3<br />
C Aus der Zeichnung erkennt man:<br />
Die Rechtecke P 2 Q 2 R 2 S 2 , P 3 Q 3 R 3 S 3 ,<br />
… erhält man <strong>durch</strong> <strong>zentrische</strong><br />
O<br />
y<br />
1<br />
<strong>Streckung</strong> des Rechtecks P 1 Q 1 R 1 S 1<br />
mit dem Zentrum B. Somit liegen<br />
alle Punkte S n auf der Halbgeraden<br />
6<br />
5<br />
C<br />
[BS 1 .<br />
4<br />
S<br />
R<br />
D Der Eckpunkt S ergibt sich als 3<br />
Schnittpunkt von [BS 1 mit [AC].<br />
S<br />
2<br />
1<br />
Durch Zeichnen entsprechender Parallelen<br />
zu den Seiten des Rechtecks<br />
P 1 Q 1 R 1 S 1 erhält man die weiteren<br />
Eckpunkte P, Q und R. Da alle<br />
1<br />
O<br />
A<br />
1<br />
P P 1 Q<br />
Rechtecke ähnlich sind, verhalten sich die Längen PQ und QR wie 2 : 1.<br />
So kann man <strong>durch</strong> Rechnung die Längen PQ und QR ermitteln:<br />
R 2<br />
R 1<br />
A P 2 Q 3 P 1 Q 2 Q 1<br />
2 3 4 5 6 7 8<br />
R 1<br />
Q 1<br />
2 3 4 5 6 7 8<br />
B<br />
9<br />
B<br />
9<br />
x<br />
x<br />
Übungen<br />
9<br />
–1 7<br />
Bezeichne die Längenmaßzahlen von<br />
PQ mit 2x und die von QR mit x.<br />
Trage alle weiteren Maßzahlen, die du<br />
mithilfe der Koordinaten der Eckpunkte<br />
A, B und C ermitteln kannst, in die<br />
Zeichnung ein.<br />
Die Dreiecke ABC und SRC sind ähnlich.<br />
Somit sind entsprechende Streckenverhältnisse<br />
gleich.<br />
Also gilt: = RS<br />
AB<br />
1<br />
h* A P Q B<br />
h<br />
Für die Maßzahlen gilt:<br />
5 – x<br />
5<br />
= 2x<br />
8<br />
a) Löse die Verhältnisgleichung und zeige, dass gilt: PQ = 4,4 LE und QR = 2,2 LE<br />
b) Löse obige Aufgabe für A(0|8); B(0|0); C(6|3) zeichnerisch. Berechne PQ und QR.<br />
y<br />
6<br />
5<br />
4<br />
3<br />
2<br />
O<br />
1<br />
S<br />
C<br />
h h*<br />
5–x 5<br />
2x<br />
R<br />
2 3 4 5 6 7 8<br />
x<br />
x<br />
9<br />
x
Einbeschreibungsaufgaben 89<br />
2 Löse die Aufgabe 1 Seite 88 zeichnerisch. Erfülle zunächst folgende Bedingungen:<br />
a) Bedingung I; II und IV.<br />
b) Bedingung II; III; IV und [P n Q n ] || [AB].<br />
8<br />
–1 10<br />
3 Dem Dreieck ABS soll ein Rechteck PQRS einbeschrieben werden. Die Strecke [PQ] soll<br />
auf [AB], der Punkt R auf [BC] und der Punkt S auf [AC] liegen. Die Seite [PQ] soll dreimal<br />
so lang sein wie die Strecke [QR].<br />
E gilt: A(0|0); B(9|0); C(5|7); QR = x LE<br />
a) Zeichne das Dreieck ABC und konstruiere das Rechteck PQRS.<br />
b) Berechne die Seitenlängen des Rechtecks und dessen Flächeninhalt.<br />
8<br />
–1<br />
–1<br />
9<br />
–1<br />
–1<br />
9<br />
–5<br />
–1<br />
8<br />
11<br />
11<br />
9<br />
4 Dem Dreieck ABC soll ein Quadrat PQRS so einbeschrieben werden, dass die Strecke<br />
[PQ] auf der Strecke [AB], der Punkt R auf [BC] und der Punkt S auf [AC] liegt.<br />
Es gilt: A(0| 1); B(10 | 1); C(6| 7)<br />
a) Zeichne das Dreieck ABC und konstruiere das Quadrat PQRS.<br />
b) Berechne die Seitenlänge des Quadrats [Ergebnis: PQ = 3,75 LE]<br />
c) Begründe, dass für den Punkt S gilt: S (x S |4,75).<br />
d) Berechne die Gleichung der Geraden AC, die Koordinate x S und die Koordinaten der<br />
Eckpunkte P, Q und R.<br />
5 Dem Dreieck ABC soll ein gleichschenkliges Dreieck PQR so einbeschrieben werden,<br />
dass folgende Bedingungen erfüllt sind: P [AC]; Q [AB]; R [BC]; [PR] || [AB]<br />
M [PR]; PM = MR; PR : MQ = 4 : 1<br />
Es gilt: A(0|0); B(10|0); C(0|8)<br />
a) Zeichne das Dreieck ABC und konstruiere das Dreieck PQR.<br />
b) Berechne die Länge PR und anschließend die Koordinaten der Punkte P; Q und R.<br />
6 Dem Drachenviereck ABCD werden Rechtecke PQRS so einbeschrieben, dass die Rechtecksseiten<br />
parallel zu den Diagonalen des Drachenvierecks verlaufen (siehe <strong>Abbildung</strong>).<br />
Es gilt: A(0|0); B(8|4); C(0|8); D(–4|4); d(P; [AC]) = x LE<br />
a) Zeichne mit einem Geometrieprogramm das Drachenviereck ABCD und ein Rechteck<br />
PQRS (z.B. für x = 2).<br />
b) Miss d (P; [AC]), d (R; [AC]) und den Flächeninhalt des Rechtecks PQRS. Verändere<br />
mit dem Zugmodus das Rechteck PQRS. Was stellst du fest?<br />
c) Bestimme die Steigungen der Geraden AB und AD.<br />
Begründe anschließend: d(R; [AC]) = 0,5x LE<br />
d) Zeige, dass mit PQ = y LE folgt: y = 8 – x<br />
e) Berechne, die Belegung von x, für die eines der Rechtecke zugleich ein Quadrat ist.<br />
Berechne den zugehörigen Flächeninhalt.<br />
f) Stelle den Flächeninhalt der Rechtecke<br />
y<br />
PQRS in Abhängigkeit von x dar.<br />
9<br />
[Ergebnis: A(x) = (–1,5x 2 C<br />
+ 12x) FE]<br />
8 xLE<br />
Berechne anschließend, um wie viel<br />
Prozent der maximale Flächeninhalt<br />
größer ist als der Flächeninhalt des<br />
R 7<br />
6<br />
5<br />
Q<br />
Quadrats in Aufgabe e).<br />
g) Die Koordinaten eines Eckpunktes des<br />
Drachenvierecks sollen so verändert<br />
D<br />
4<br />
3<br />
2<br />
yLE<br />
B<br />
werden, dass die einbeschriebenen<br />
S 1 P<br />
Rechtecke symmetrisch zur y-Achse<br />
sind.<br />
–4 –3 –2 –1 O A 1 2 3 4 5 6 7 8 x
90 Der Pantograf<br />
1 1603 erfuhr Christoph Scheiner in Dillingen von einem Maler, dass dieser ein Gerät besitze,<br />
das jedes Bild genau nachzeichnen und zusätzlich sogar im Maßstab vergrößern oder<br />
verkleinern könne. Wie das Gerät funktioniert, verriet der Maler nicht.<br />
Dies veranlasste Scheiner selbst nach einer Lösung zu suchen. Er erfand den so genannten<br />
Pantograf 1 oder „Storchenschnabel“.<br />
Das Gerät besteht aus vier Holz- oder Metallstäben, die <strong>durch</strong> Gelenke zu einem veränderbaren<br />
Parallelogramm verbunden sind. Der so genannte Schwenkpunkt Z bleibt fest.<br />
Mit dem Fahrstift P fährt man die Linien<br />
einer Zeichnung nach. Der Zeichenstift Q<br />
erstellt dann ein im Maßstab vergrößertes<br />
Bild. Vertauscht man Fahrstift und Zeichenstift,<br />
kann man ein im Maßstab verkleinertes<br />
Bild zeichnen.<br />
Pantografen werden immer noch von Z<br />
P<br />
Q<br />
technischen Zeichnern und Architekten<br />
verwendet, sie werden eingesetzt in Graviermaschinen<br />
und in Pantografstickmaschinen<br />
für Buntstickereien.<br />
a)<br />
H’<br />
H<br />
P<br />
Q<br />
Z<br />
Begründe: Die Punkte Z, P und Q müssen auf einer Geraden liegen<br />
b) Bei dem mit einem Geometrieprogramm erstellten Pantografen im Bild oben beträgt<br />
die Länge ZH das Dreifache der Länge ZH. Der Punkt P simuliert den Fahrstift.<br />
Begründe, dass der Pantograf auf das Dreifache vergrößert, dass also gilt:<br />
ZQ = 3 · ZP (Hinweis: Betrachte die Dreiecke ZPH und ZQH).<br />
c) In welchem Maßstab vergrößert bzw. verkleinert der dargestellte Pantograf unten im<br />
Bild, wenn der Fahrstift im Punkt P montiert ist?<br />
I II III<br />
Z<br />
Q<br />
P<br />
d) Baue dir selbst einen Pantografen z.B. mithilfe von Metallbauteilen und Schrauben<br />
oder festen Folienstreifen und Druckknöpfen.<br />
e) Versuche mit einem Geometrieprogramm einen Pantografen zu konstruieren, der einen<br />
gegebenen Kreis im Maßstab 1 : 3 verkleinert.<br />
f) Nenne eine Maschine, bei der der eingebaute Pantograf im Maßstab 1 : 1 arbeitet.<br />
1<br />
Allesschreiber<br />
Z P Q<br />
Z<br />
Q<br />
P
Vom Bild zur Karte 91<br />
1<br />
N<br />
N<br />
Schrägluftbild Schrägluftbild aus aus 400 400 m Höhe m Höhe.<br />
NN<br />
N<br />
Klosteranger<br />
Sportplatz<br />
Strandbad-<br />
West<br />
527<br />
Fähranleger<br />
Torhalle<br />
Kloster<br />
Senkrechtluftbild<br />
aus 1000 m Höhe<br />
Senkrechtluftbild aus 1000 m Höhe.<br />
Spielplatz<br />
Turnhalle<br />
Sportplatz<br />
Irmengard-<br />
Berufsschule<br />
Fraueninsel<br />
0 50 100 150 200<br />
m<br />
Maßstab 1 :<br />
öffentliches<br />
Gebäude<br />
historisches<br />
Gebäude<br />
Kirche<br />
Wohngebäude<br />
(z. T. Geschäfte)<br />
Gasthof, Café<br />
geschlossene<br />
Baumgruppe<br />
Grünfläche<br />
mit Parkbäumen<br />
Friedhof<br />
Höhe in Meter<br />
über Normalnull<br />
(NN)<br />
Schifffahrtslinie<br />
Sturmwarnsignal<br />
Denkmal<br />
Tiefenlinie<br />
a) Wo könnte beim Senkrechtluftbild das Zentrum einer <strong>zentrische</strong>n <strong>Streckung</strong> sein?<br />
b) Die Fraueninsel hat ihre längste Ausdehnung in Nord-Südrichtung mit ca. 600 m. Auf<br />
dem Bildschirm der Kamera erscheint davon ein Bild von 9,0 cm Länge.<br />
Ermittle den Faktor k der zugehörigen <strong>zentrische</strong>n <strong>Streckung</strong>.<br />
c) Ermittle den Maßstab der unteren Karte.<br />
A 1 : 7500 B 1 : 10000 C 1 : 25000<br />
527<br />
3m
92 Zentrische <strong>Streckung</strong> mithilfe von Vektoren<br />
5<br />
–4 10<br />
–3<br />
1 a) Der Punkt P(7|3) wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z(3|1) und dem<br />
<strong>Streckung</strong>sfaktor k = 1,5 (k = –1,5) auf den Punkt P abgebildet.<br />
ƒƒ© ƒƒ©<br />
Ermittle die Koordinaten der Pfeile ZP und ZP <strong>durch</strong> Zeichnung.<br />
b)<br />
Mit den Koordinaten des<br />
ƒƒ©<br />
Pfeils ZP sowie dem<br />
<strong>Streckung</strong>sfaktor k müsste man doch<br />
ƒƒ©<br />
die Koordinaten des Pfeils ZP auch<br />
<strong>durch</strong> Rechnung bestimmen<br />
können.<br />
Wie beurteilst du die Aussage von Sabrina?<br />
c) Ergänze jeweils die Platzhalter in deinem Heft.<br />
Z(4|2) : k = 2<br />
∂ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ©<br />
Z(4|2) : k = –2<br />
∂ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ©<br />
I P(6|3) P(x|y) II P(6|3) P(x|y)<br />
y<br />
y<br />
4<br />
k>0<br />
P’<br />
k0 Q’<br />
k
Zentrische <strong>Streckung</strong> mithilfe von Vektoren 93<br />
<strong>zentrische</strong><br />
<strong>Streckung</strong><br />
mithilfe eines<br />
Vektors<br />
Durch eine <strong>zentrische</strong> <strong>Streckung</strong> mit<br />
dem <strong>Streckung</strong>sfaktor k wird der Pfeil<br />
ƒƒ©<br />
PQ = ( x<br />
ƒƒ©<br />
v )auf den Bildpfeil PQ ƒƒƒ<br />
y<br />
abgebildet.<br />
Die Koordinaten des Bildpfeils<br />
erhält man <strong>durch</strong> Multiplikation der<br />
Koordinaten des Urpfeils mit dem Faktor<br />
k.<br />
ƒƒƒƒƒ© ƒƒ©<br />
PQ = k · PQ<br />
(<br />
v x )= k · (<br />
v x<br />
)= (<br />
k · v x<br />
v y v y k · v y<br />
)<br />
ƒƒ© ƒ©<br />
Mit PQ v und PQ ƒƒƒ ƒƒ© ƒ©<br />
v folgt für die<br />
ĩ<br />
<strong>zentrische</strong> <strong>Streckung</strong> eines Vektors v :<br />
v ƒ© = k · ƒ©<br />
v<br />
y<br />
4<br />
3<br />
P’<br />
1<br />
O<br />
–1<br />
P<br />
1<br />
v’<br />
v’ x<br />
v<br />
v x<br />
Z<br />
Q<br />
v y<br />
Q’<br />
v’ y<br />
x<br />
Übungen<br />
2 Ermittle die fehlenden Koordinaten bzw. den fehlenden Wert für k in deinem Heft.<br />
a) (<br />
x<br />
)= 2 · (<br />
3<br />
) b) (<br />
x<br />
)= –1,5 · (<br />
3<br />
) c) (–5<br />
)= k · (<br />
2<br />
y –1<br />
y<br />
2,5<br />
4 y )<br />
d) (<br />
6<br />
)= –3 · (<br />
x<br />
) e) (–7,5)= –0,5 · (<br />
x<br />
) f) (<br />
x<br />
3<br />
)= k · ( )<br />
y<br />
3,5<br />
2,1<br />
y<br />
–8,1<br />
1<br />
2,7<br />
L –2; –2,5; –4,5; –1,6; 6; –2; –3,75; 15; –4,2; –1; –3; –10,5<br />
3 Der Punkt P(–3|1) wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z(–5|–2) und dem<br />
<strong>Streckung</strong>sfaktor k = 1,5 auf den Punkt P(x|y) abgebildet. So kann man die Koordinaten<br />
von P berechnen.<br />
P’(x’|y’)<br />
y<br />
2<br />
P’(x’|y’)<br />
y<br />
2<br />
P(–3|1)<br />
1<br />
P(–3|1)<br />
1<br />
Berechnung<br />
der<br />
Koordinaten<br />
von Punkten<br />
–5 –4 –3 –2 –1 O x<br />
–5 –4 –3 –2 –1<br />
–1<br />
Z(–5|–2)<br />
Z(–5|–2)<br />
O<br />
–1<br />
1. Möglichkeit: Pfeilkette<br />
ƒƒƒ© ƒƒ©<br />
ƒƒƒ©<br />
OP = OZ ZP<br />
ƒƒƒ© ƒƒ© ƒƒ©<br />
OP = OZ k · ZP<br />
(<br />
x)= (–5<br />
) 1,5 · (–3 + 5)<br />
y –2<br />
x = –5 + 1,5 · 2<br />
Ÿ y = –2 + 1,5 · 3<br />
1 + 2<br />
2. Möglichkeit: <strong>Abbildung</strong>svorschrift<br />
ƒƒƒ© ƒƒ©<br />
ZP = k · ZP<br />
(<br />
x + 5)= 1,5 · (–3 + 5)<br />
y + 2<br />
x + 5 = 1,5 · 2<br />
Ÿ y + 2 = 1,5 · 3<br />
1 + 2<br />
a) Zeige <strong>durch</strong> Rechnung, dass sich folgende Koordinaten für P ergeben: P(–2|2,5).<br />
b) Berechne die Koordinaten von P für k = –3; Z(0,5|1); P(–1|2).
94 Zentrische <strong>Streckung</strong> mithilfe von Vektoren<br />
4 Der Punkt P wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum Z und dem Faktor k auf<br />
den Punkt P abgebildet. Berechne die fehlenden Werte in deinem Heft.<br />
Z(x Z |y Z ) k P(x|y) P(x|y)<br />
a) (1|1) 2 (3|0) (■|■)<br />
b) (–3|–1) –3 (■|■) (–6|0,5)<br />
c) (–4|1) ■ (–1|2,5) (0|3)<br />
d) (■|■)<br />
1<br />
3<br />
(0|8) (6|2)<br />
e) (2|■) –1,5 (■|–2) (0,5|3)<br />
f) (–4|1) ■ (–1|2,5) (■|3)<br />
g) (–4|5) 0,75 (■|3,5) (–4|■)<br />
10<br />
–4 7<br />
–2<br />
5 Die Strecken [AB n ] werden <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong>en mit den <strong>Streckung</strong>szentren Z n<br />
und dem <strong>Streckung</strong>sfaktor k (k 0) auf die Strecke [AB] abgebildet. Die Punkte<br />
B n (x|3) liegen auf der Geraden g mit y = 3.<br />
Es gilt: A(–1|3); B n (x|3); A(1|–1); B(6|–1)<br />
a) Zeichne mit einem Geometrieprogramm die Strecken [AB]; [AB 1 ] und [AB 2 ] für<br />
x = 0 und für x = 2. Markiere die zugehörigen Zentren Z 1 und Z 2 .<br />
b) Berechne jeweils den <strong>Streckung</strong>sfaktor k in Aufgabe a) und die Koordinaten der<br />
zugehörigen Zentren Z 1 und Z 2 .<br />
c) Stelle in deinem Heft den <strong>Streckung</strong>sfaktor<br />
k in Abhängigkeit von x dar.<br />
5<br />
[Ergebnis: k = x + 1 ]<br />
d) Für zwei Belegungen von k lassen sich<br />
keine <strong>zentrische</strong> <strong>Streckung</strong>en angeben.<br />
Finde diese Werte mithilfe des Geometrieprogramms.<br />
Begründe die gefundenen Werte.<br />
e) Begründe: Die Zentren Z n liegen auf<br />
einer Geraden h. Gib die Gleichung an.<br />
f) Ermittle <strong>durch</strong> Zeichnung die x-Koordinate<br />
von B 3 für Z 3 (–3|7) Berechne<br />
anschließend den Wert von x und den<br />
<strong>Streckung</strong>sfaktor k.<br />
y<br />
x-Koordinate des Punktes B<br />
Aktueller Wert: 0,7408<br />
<strong>Streckung</strong>sfaktor k<br />
Aktueller Wert: 2,872<br />
Z n<br />
A B n<br />
1<br />
–1 O<br />
–1<br />
1<br />
A’ B’<br />
x<br />
Einer der vier Ganoven Atze, Bodenlos, Convex und Dodl hat einen Münzautomaten aufgebrochen<br />
und das Geld in seinen Hosentaschen versteckt. Deshalb hat er das größte<br />
Gewicht. Wer ist es?
<strong>Abbildung</strong> einer Geraden <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> 95<br />
1 Die Gerade g mit der Gleichung y = 0,5x + 1 wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit dem<br />
Zentrum Z(2|1) und dem <strong>Streckung</strong>sfaktor k = 2,5 auf die Bildgerade g abgebildet. So<br />
kann man die Gleichung von g berechnen.<br />
y<br />
4<br />
3<br />
2<br />
1<br />
O<br />
–1<br />
1<br />
P’(x’|y’) g’<br />
g<br />
P(x|0,5x+1)<br />
Z(2|1)<br />
2 3 4 5<br />
x<br />
Für alle Punkte P(x|y) auf der Geraden<br />
g mit y = 0,5x + 1 gilt:<br />
P(x|0,5x + 1)<br />
Mit der Pfeilkette folgt:<br />
ƒƒƒ© ƒƒ© ƒƒƒ©<br />
OP = OZ ZP<br />
ƒƒƒ© ƒƒ© ƒƒ©<br />
OP = OZ k · ZP<br />
(<br />
x)= (<br />
2<br />
) 2,5 · (<br />
x – 2<br />
y 1 0,5x + 1 – 1)<br />
x = 2 + 2,5x – 5<br />
Ÿ y = 1 + 1,25x<br />
x = 2,5x – 3<br />
Ÿ y = 1,25x + 1<br />
Das Ziel ist es, einen Zusammenhang zwischen den Koordinaten x und y der Punkte<br />
P(x|y) auf der Geraden g zu finden. Deshalb eliminiert (entfernt) man die Variable<br />
x aus dem Gleichungssystem.<br />
Dazu löst man eine Gleichung nach x<br />
auf.<br />
Den Term für x setzt man in die andere<br />
Gleichung ein.<br />
Lässt man die Apostrophen weg, dann<br />
lautet die Gleichung der Bildgeraden:<br />
x + 3<br />
2,5 = x<br />
x + 3<br />
Ÿ y = 1,25 · 2,5 + 1<br />
y = 0,5(x + 3) + 1<br />
y = 0,5x + 2,5<br />
g: y = 0,5x + 2,5<br />
a) Vergleiche die Berechnung der Gleichung der Bildgeraden im grünen Kasten mit der<br />
Berechnung in Aufgabe 4 Seite 74. Nenne die Unterschiede.<br />
ƒƒƒ© ƒƒ©<br />
b) Berechne die Gleichung der Bildgeraden mithilfe der Vorschrift ZP = k · ZP .<br />
Parameterverfahren<br />
Durch ein Gleichungssystem mit der Variablen x und y und der weiteren Variablen<br />
(dem Parameter) x kann man die Gleichung einer Bildgeraden ermitteln. Diese erhält<br />
man <strong>durch</strong> Eliminieren des Parameters x aus dem Gleichungssystem. Ein solches<br />
Verfahren nennt man Parameterverfahren.<br />
Übungen<br />
6<br />
–3 7<br />
–4<br />
2 Die Gerade g wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> auf die Gerade g abgebildet. Zeichne die<br />
Geraden g und g. Berechne die Gleichung der fehlenden Geraden.<br />
a) g: y = x – 1; Z(0|1); k = –2 b)g: y = x – 1; Z(0|1); k = –2<br />
c) g: y = 2x; Z(3|0); k = – 1<br />
1<br />
3<br />
d) g: y = 2x; Z(3|0); k = 3<br />
e) g: y = –0,5x + 1; Z(2|3); k = 1,5 f) g: 4x – 2y + 5 = 0; Z(1|2); k = –0,5<br />
L (nur y-Achsenabschnitte): –0,5; 8; 5; –1,25; 6; –8; –4
96 Teilpunkt einer Strecke<br />
7<br />
–2<br />
9<br />
1 Der Punkt T soll die Strecke [AB] so teilen, dass gilt: AT : TB = 5 : 2<br />
Es gilt: A(2|–1); B(8,3|6,7)<br />
a) Ermittle die Koordinaten des Teilpunktes T <strong>durch</strong> Zeichnung (siehe Aufgabe 2 S. 72).<br />
b) Vergleiche die gefundenen Koordinaten von T mit denen deiner Nachbarn.<br />
2 So kann man die Koordinaten des Teilpunktes T in Aufgabe 1 berechnen.<br />
y<br />
y<br />
8<br />
B(8,3|6,7)<br />
8<br />
B(8,3|6,7)<br />
6<br />
4<br />
2<br />
O<br />
–2 A(2|–1)<br />
T(x|y)<br />
5 Teile<br />
7 Teile<br />
2 Teile<br />
4 6 8 10<br />
x<br />
6<br />
4<br />
2<br />
O<br />
–2 A(2|–1)<br />
T(x|y)<br />
4 6 8 10<br />
5 Teile 2 Teile<br />
x<br />
1. Möglichkeit<br />
ƒƒ© ƒƒ©<br />
Pfeilkette: OT = OA <br />
(<br />
x<br />
)= (<br />
2 5<br />
) · (<br />
8,3 – 2<br />
)<br />
y<br />
–1<br />
7<br />
5<br />
7<br />
6,7 + 1<br />
ƒƒ©<br />
· AB<br />
2. Möglichkeit:<br />
ƒƒ©<br />
<strong>Abbildung</strong>svorschrift: AT =<br />
(<br />
x – 2 5<br />
)= · (<br />
8,3 – 2<br />
y + 1 7 6,7 + 1 )<br />
5<br />
7<br />
ƒƒ©<br />
· AB<br />
a) Zeige, dass der Teilpunkt T folgende Koordinaten hat: T(6,5|4,5)<br />
b) Gib weitere Möglichkeiten an, die Koordinaten des Teilpunktes T zu berechnen.<br />
Übungen<br />
8<br />
–7 11<br />
–4<br />
9<br />
–4 7<br />
–3<br />
3 Der Punkt T ist Teilpunkt der Strecke [AB]. Ermittle <strong>durch</strong> Zeichnung und <strong>durch</strong> Rechnung<br />
die Werte der Platzhalter in deinem Heft.<br />
a) A(–6|0,5); B(4|5,5); AT : TB = 2 : 3; T(■|■)<br />
b) A(10|1); B(2|7); AT : TB = 5 : 3; T(■|■)<br />
c) A(0|–3); B(–4,5|–7,5); AT : TB = ■ : ■; T(–2,5|–1,75)<br />
d) A(1|–3); B(6|2); AT : TB = ■ : ■; T(4,5|■)<br />
e) A(–5|3); B(1|6); AT : TB = ■ : ■; T(■|3,5)<br />
4 Gegeben sind eine Gerade g, eine Gerade h und ein Punkt Z.<br />
Es gilt: Z(2|2); g: y = 0,5x – 2; h: y = –0,5x + 8<br />
a) Zeichne den Punkt Z sowie die Geraden g und h.<br />
b) Die Punkte P n (x|0,5x – 2) auf der Geraden g sind Endpunkte von Strecken [P n Q n ],<br />
für die gilt: P n Z : ZQ n = 2 : 3.<br />
Zeichne die Strecken [P 1 Q 1 ] für x = 4 und [P 2 Q 2 ] für x = 6.<br />
c) Begründe: Die Punkte Q n liegen auf einer Geraden g. Ermittle ihre Gleichung.<br />
[Ergebnis: g : y = 0,5x + 3]<br />
d) Es gibt eine Strecke [P 0 Q 0 ] bei der der Punkt Q 0 zusätzlich auf der Geraden h liegt.<br />
Berechne die Koordinaten dieses Punktes.<br />
e) Löse die Aufgaben a) bis d) für P n Z : ZQ n = 3 : 2.
Schwerpunkt eines Dreiecks 97<br />
Schwerpunkt<br />
1 a) Schneide aus Pappe ein Dreieck ABC<br />
aus. Finde einen Punkt S so, dass das<br />
Dreieck im Gleichgewicht ist, wenn du<br />
es mit einem Bleistift in diesem Punkt<br />
unterstützt. Einen solchen Punkt nennt<br />
man Schwerpunkt.<br />
b) Zeichne die Halbgeraden [AS, [BS<br />
und [CS. Diese schneiden die Dreiecksseiten<br />
in besonderen Punkten.<br />
Welche Eigenschaften haben diese?<br />
Ich finde<br />
den Schwerpunkt<br />
so.<br />
c) Jede Dreieckfläche kann man <strong>durch</strong><br />
eine Summe vieler Rechtecksflächen<br />
annähern. Die Schwerpunkte der Rechtecksflächen<br />
kann man leicht finden.<br />
Begründe, dass der Schwerpunkt des<br />
Dreiecks ABC auf der Strecke [CM c ],<br />
der so genannten Seitenhalbierenden<br />
s c , liegen muss. Der Punkt M c ist Mittelpunkt<br />
der Strecke [AB].<br />
d) Stelle Überlegungen an, auf welchen<br />
weiteren Strecken der Schwerpunkt<br />
noch liegen muss.<br />
2 a) Zeichne mit einem Geometrieprogramm<br />
ein Dreieck ABC und die drei Seitenhalbierenden.<br />
b) Übertrage die Tabelle in dein Heft und<br />
ergänze sie. Was stellst du fest?<br />
C<br />
S 2<br />
S 1<br />
A M c B<br />
C<br />
1,8cm<br />
M b<br />
M a<br />
3cm<br />
S<br />
1,5cm<br />
A<br />
M c<br />
B<br />
SA SM a SB SM b SC SM c<br />
in cm in cm in cm in cm in cm in cm<br />
■ ■ ■ ■ ■ ■ ■ ■ ■<br />
3 Die Punkte M a und M b sind Mittelpunkte der Seiten [BC] und [AC] eines Dreiecks ABC.<br />
SA<br />
SM a<br />
SB<br />
SM b<br />
SC<br />
SM c<br />
a) Begründe: Das Dreieck M b M a C<br />
kann <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> mit<br />
dem Zentrum C und k = 2 auf das<br />
Dreieck ABC abgebildet werden.<br />
b) Begründe mithilfe von a), dass gilt:<br />
[M b M a ] [AB] und M b M a = 0,5 · AB<br />
b) Begründe mithilfe von b):<br />
Das Dreieck M a M b S kann <strong>durch</strong><br />
<strong>zentrische</strong> <strong>Streckung</strong> mit dem Zentrum<br />
S und dem Faktor k* auf das<br />
Dreieck ABS abgebildet werden.<br />
Gib k* an.<br />
d) Begründe mithilfe von b), dass gilt:<br />
SA 2 SB<br />
= und = 2 SM a 1 SM b 1<br />
A<br />
A<br />
M b<br />
M b<br />
S<br />
S<br />
C<br />
M a<br />
M a<br />
B<br />
B
98 Schwerpunkt eines Dreiecks<br />
4 Die Punkte M b und M c sind Mittelpunkte der Seiten [AC] und [AB] des Dreiecks ABC.<br />
a) Zeige wie in Aufgabe 3 Seite 97,<br />
dass gilt:<br />
S*B 2<br />
S*M =<br />
b 1<br />
M b<br />
S<br />
C<br />
b) Begründe, dass aus a) und aus Aufgabe<br />
3d Seite 97 folgt: S = S*<br />
A<br />
M c<br />
B<br />
Seitenhalbierende<br />
Schwerpunkt<br />
Die Verbindungsstrecken der Seitenmittelpunkte<br />
mit den gegenüberliegenden<br />
Dreiecksseiten bezeichnet man<br />
als Seitenhalbierende (Schwerlinien).<br />
Diese schneiden sich in einem Punkt,<br />
dem Schwerpunkt S. Er teilt jede Seitenhalbierende<br />
im Verhältnis 2:1.<br />
A<br />
s b<br />
S<br />
M c<br />
s c<br />
S n<br />
C<br />
s a<br />
M a<br />
B<br />
Übungen<br />
7<br />
–3 9<br />
9<br />
–5 9<br />
–6<br />
11<br />
10<br />
5 Zeichne das Dreieck ABC und konstruiere den Schwerpunkt.<br />
a) a = 6 cm; b = 5 cm; c = 8 cm b) b = 6,4 cm; c = 7 cm; a = 60°<br />
c) A(1|–2); B(7|0); C(5|5) d) A(4|0); B(8|3); C(5,5|6)<br />
6 Der Punkt S ist Schwerpunkt des Dreiecks ABC. Ermittle <strong>durch</strong> Zeichnung die Koordinaten<br />
der fehlenden Eckpunkte bzw. des fehlenden Schwerpunktes.<br />
a) A(0|–4); B(6|–2); S(3|0) b) A(–4|1); C(0|6); S(–1|2,5)<br />
c) A(–4|–4); M [AB] (–1|–5); S(–1|–3) d) A(2,5|2); M [AC] (4|5); S(5,5|4)<br />
7 Die Punkte A n , B n und C n sind Eckpunkte von gleichseitigen Dreiecken A n B n C n . Die Punkte<br />
A n (x|1) liegen auf der Geraden g mit y = 1. Die Punkte M n (x|3x + 1) auf der Geraden<br />
g mit y = 3x + 1 sind Mittelpunkte der Dreiecksseiten [B n C n ]. Sie haben die gleiche Abszisse<br />
x wie die Punkte A n .<br />
a) Zeichne für x = 1 und x = 2 die<br />
C y n<br />
M n B n<br />
zugehörigen Dreiecke A 1 B 1 C 1 und<br />
5<br />
A 2 B 2 C 2 . Zeichne die zugehörigen<br />
Schwerpunkte S 1 und S 2 ein. Berechne<br />
4<br />
ihre Koordinaten.<br />
b) Für welche Belegungen von x gibt es<br />
3<br />
Dreiecke A n B n C n mit dem Umlaufssinn<br />
entgegen dem Uhrzeiger?<br />
2<br />
c) Zeige, dass für die Koordinaten der<br />
Schwerpunkte gilt: S n (x|2x + 1).<br />
1<br />
A<br />
Verwende zur Berechnung die Pfeilkette<br />
n<br />
ƒƒƒ© ƒƒƒ© ƒƒƒ©<br />
OS n<br />
= OA n AS n .<br />
–2 –1 O 1 2 3 4 x<br />
d) Gib die Gleichung des Graphen s an,<br />
auf dem die Schwerpunkte S n liegen.<br />
Zeichne den Graphen s ein.
Koordinaten des Schwerpunkts eines Dreiecks 99<br />
1 a) Zeichne mit einem Geometrieprogramm<br />
ein Dreieck ABC und den<br />
zugehörigen Schwerpunkt S.<br />
Es gilt: A(1|2); B(10|0); C(4|7).<br />
Vergleiche die Koordinaten von S mit<br />
den Koordinaten der Eckpunkte.<br />
b) Lass die Koordinaten der Eckpunkte<br />
und des Schwerpunktes S anzeigen.<br />
Hebe die Fixierung z.B. des Eckpunktes<br />
C an das Gitter auf und verändere<br />
mit dem Zugmodus dessen Lage. Beobachte<br />
wieder die angezeigten Koordinaten<br />
der Eckpunkte und die des<br />
Schwerpunktes S. Was stellst du fest?<br />
y<br />
9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
A(1|2)<br />
O 1<br />
x-Koordinate von A<br />
Aktueller Wert: 1<br />
x-Koordinate von C<br />
Aktueller Wert: 5,2<br />
C<br />
S<br />
x-Koordinate von B<br />
Aktueller Wert: 10<br />
x-Koordinate von S<br />
Aktueller Wert: 5,4<br />
M<br />
2 3 4 5 6 7 8 9<br />
B(10|0)<br />
10 x<br />
2 So kann man die Koordinaten des Schwerpunktes S (x s |y s ) eines Dreiecks ABC in Abhängigkeit<br />
von den drei Eckpunktskoordinaten berechnen.<br />
y<br />
9<br />
8<br />
7<br />
C(x C |y C )<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
A(x A |y A ) S M<br />
–1 O<br />
–1<br />
1 2 3 4 5 6 7 8<br />
–2<br />
B(x B |y B )<br />
x<br />
Für den Mittelpunkt M (x M |y M ) der<br />
Strecke [BC] gilt:<br />
x<br />
M ( B + x C y<br />
| B + y C<br />
2 2<br />
)<br />
Der Schwerpunkt S teilt die Strecke<br />
[AM] im Verhältnis 2:1<br />
ƒƒ© ƒƒƒ©<br />
Es gilt: AS = 2 · SM<br />
x B + x C<br />
(<br />
x S<br />
–<br />
–<br />
x A<br />
2 x<br />
) = 2 ·<br />
(<br />
s<br />
y S<br />
– y A y B + y C<br />
– )<br />
2 y s<br />
x S<br />
– x A = x B + x C – 2x S | + 2x S + x A<br />
Ÿ y S<br />
– y A = y B + y C – 2y S | + 2y S + y A<br />
3x s = x A + x B + x C<br />
Ÿ 3y S = y A + y B + y C<br />
x<br />
x S = ; y S = y A + x B + x C<br />
A + y B + y C<br />
3<br />
3<br />
Koordinaten<br />
des Schwerpunktes<br />
eines<br />
Dreiecks<br />
Für die Koordinaten des Schwerpunktes<br />
S (x S |y S ) eines Dreiecks ABC gilt:<br />
x<br />
S ( A + x B + x C y<br />
| A + y B + y C<br />
)<br />
3<br />
3<br />
y<br />
C(x C |y C )<br />
2<br />
S(x S |y S )<br />
A(x A |y A )<br />
1<br />
B(x B |y B )<br />
–2 –1 O 1 2 3 4 5 6 7<br />
x<br />
Übung<br />
3 Der Punkt S ist Schwerpunkt des Dreiecks ABC. Berechne die fehlenden Koordinaten.<br />
a) A(–3|1); B(–0,5|2); C(–1|4,5); S(x S |y S )<br />
b) A(2,5|2); B(5|4); C(0|9); S(x S |y S )<br />
c) A(–5|–3); B(–2|1); C(–1,5|x C ); S(x S |1)<br />
d) A(0,5|1); B(x B |3); C(3|5); S(1|y S )
100 Vermischte Übungen<br />
9<br />
–2 11<br />
9<br />
–8 5<br />
–5<br />
1 Im Dreieck ABC mit dem Schwerpunkt S gilt: A(1|2); B(10|–1); S(5|3)<br />
a) Zeichne das Dreieck ABC.<br />
b) Berechne die Koordinaten des Eckpunktes C.<br />
c) Berechne die Koordinaten der Mittelpunkte M a , M b und M c der Seiten des Dreiecks.<br />
d) Berechne den prozentualen Anteil des Flächeninhalts des Dreiecks M a M b M c am<br />
Flächeninhalt des Dreiecks ABC.<br />
2 Das Dreieck ABC wird <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong>en mit den <strong>Streckung</strong>szentrum Z 1 und<br />
dem <strong>Streckung</strong>sfaktor k 1 auf das Dreieck A*B*C* abgebildet.<br />
Es gilt: A(1|2); B(3|0,5); C(4|3); k 1 = 2<br />
a) Zeichne das Dreieck ABC und das Dreieck A*B*C*. Berechne die Koordinaten der<br />
Bildpunkte A*, B* und C*.<br />
Z 2 (–2|3); k<br />
ƒƒƒƒƒƒƒƒƒ 2 = –0,75<br />
b) DA*B*C* ∂ƒƒƒƒƒƒƒƒ ƒƒƒƒ© DABC.<br />
Berechne die Koordinaten der Bildpunkte A, B und C.<br />
[Ergebnis: A (–2|6); B(–5|8,25); C(–6,5|4,5)]<br />
c) Das Dreieck ABC lässt sich mit einem Zentrum Z und einem <strong>Streckung</strong>sfaktor k direkt<br />
auf das Dreieck ABC abbilden. Ermittle <strong>durch</strong> Zeichnung die Koordinaten von Z.<br />
d) Berechne den <strong>Streckung</strong>sfaktor k und vergleiche mit den Faktoren k 1 und k 2 . Was stellst<br />
du fest?<br />
e) Berechne die Koordinaten von Z.<br />
f) Ermittle Beziehungen zwischen den Flächeninhalten der drei Dreiecke ABC, A*B*C*<br />
und ABC.<br />
7<br />
–7<br />
13<br />
3 Die Punkte C n von gleichschenkligen Dreiecken AB n C n mit der Basis [AB n ] liegen auf der<br />
Geraden g mit y = 6. Die Dreiecke AB n C n werden <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> auf Dreiecke<br />
AB n C n abgebildet. Es gilt: A(0|0); B n (x|0); Z(6|–3); k = –<br />
1<br />
3.<br />
a) Zeichne für x = 6 und für x = 9 die Dreiecke AB 1 C 1 und AB 2 C 2 und die zugehörigen<br />
Bilddreiecke. Berechne die Koordinaten der Eckpunkte.<br />
b) Stelle die Koordinaten der Bildpunkte B n und C n in Abhängigkeit von x dar.<br />
c) Zeichne in den Dreiecken aus Aufgabe a) die Schwerpunkte ein und berechne deren<br />
Koordinaten. Gib die Gleichungen der Geraden an, auf denen die Schwerpunkte S n bzw.<br />
die Schwerpunkte S n liegen.<br />
d) Berechne die Koordinaten des Umkreismittelpunktes M 1 des Dreiecks AB 1 C 1 und des<br />
Dreiecks AB 1 C 1 .<br />
e)<br />
Für x = 12 haben Ur- und<br />
Bilddreieck eine ganz besondere Form!<br />
9<br />
–6 6<br />
–5<br />
4 Gegeben ist das Geradenbüschel g(m) mit y = m(x – 3) + 2.<br />
a) Gib die Koordinaten des Büschelpunktes B an.<br />
b) Überprüfe <strong>durch</strong> Rechnung, ob die Gerade g 1 mit y = –2x + 8 Element des Büschels<br />
ist. Zeichne den Punkt B und die Gerade g 1 .<br />
c) Der Punkt B und das Geradenbüschel g(m) werden <strong>durch</strong> <strong>zentrische</strong> <strong>Streckung</strong> abgebildet.<br />
Die Gerade g 1 ist Element des Büschels g(m). Zeichne die Gerade g 1 und den<br />
Punkt B. Es gilt: Z(2|1); k = –3.<br />
d) Berechne die Koordinaten von B und die Gleichung von g 1 .<br />
e) Gib die Gleichung des Geradenbüschels g(m) an.<br />
f) Überprüfe, ob die Gerade g 2 mit y = 0,5x – 1,5 Element des Büschels g(m) ist.<br />
g) Zeichne die Gerade g 2 . Gib die Gleichung von g 2 an. Was stellst du fest?
Kollisionsgefahr auf See 101<br />
1 Nicht nur auf den engen Wasserstraßen in Küstennähe, sondern auch auf den riesigen Weiten<br />
der offenen See kann es zu Kollisionen zwischen Schiffen kommen.<br />
a) Nenne mögliche Gründe.<br />
b) Das geradlinig nach Osten fahrende Schiff A peilt ein Schiff B an. Der Radarschirm<br />
zeigt die Entfernung der beiden Schiffe und den Winkel zwischen Fahrtrichtung und<br />
Peilung an. Die Ergebnisse von drei Peilvorgängen sind – anders als in Wirklichkeit –<br />
ĩ<br />
<strong>durch</strong> die drei Vektoren v 1 = (<br />
3,6 sm Ost ĩ<br />
), v 2 = (<br />
1,6 sm Ost ĩ<br />
) und v 3 = (<br />
0,8 sm Ost<br />
)<br />
12,6 sm Süd 5,6 sm Süd<br />
2,8 sm Süd<br />
dargestellt.<br />
Ein Zusammenstoß droht dann, wenn die Peilung „steht“ ist, d.h. der Winkel zwischen<br />
den Fahrtrichtungen der beiden Schiffe immer gleich bleibt. Ist dies für die Schiffe A<br />
und B der Fall? Begründe.<br />
ĩ<br />
v 1<br />
α<br />
ĩ<br />
v 2<br />
β<br />
ĩ<br />
v 3<br />
γ<br />
9<br />
8<br />
1 sm<br />
(Seemeile)<br />
≈ 1,9 km<br />
1 Knoten = 1 sm h<br />
2 Die beiden Schiffe Pommern (P) und Bavaria (B) sind in der Ostsee unterwegs. Das Schiff<br />
Pommern befindet sich um 10:00 Uhr in Position P(20|15). Dessen Kurs beträgt konstant:<br />
10 sm Ost<br />
ĩ h<br />
v 1 =<br />
( 7,5 sm Nord )<br />
h<br />
Das Schiff Bavaria hat um 11:00 Uhr die Position B(30|75). Es fährt mit konstanter<br />
Geschwindigkeit Richtung Südost.<br />
a) Zeichne die Positionen der beiden Schiffe um 10:00 Uhr und deren Kursrichtung in ein<br />
Koordinatensystem ein (für die Zeichnung: 10 sm 1 cm; y-Achse zeigt nach Norden).<br />
b) Ermittle <strong>durch</strong> Zeichnung und Rechnung die Position des Schiffes Pommern um 12:00<br />
Uhr. Ermittle mithilfe der Maße in der Zeichnung die Geschwindigkeit in Knoten.<br />
c) Ermittle <strong>durch</strong> Zeichnung und <strong>durch</strong> Rechnung die Koordinaten des möglichen Kollisionspunktes<br />
S, wenn beide Schiffe ihre Fahrtrichtung konstant beibehalten.<br />
[Ergebnis: S(60|45)]<br />
d) Warum muss es nicht zum Zusammenstoß kommen?<br />
e) Um 12:00 Uhr führt das Schiff Pommern eine Peilung <strong>durch</strong>. Es ortet das Schiff Bavaria<br />
ĩ<br />
in Richtung des Vektors v 2 = (<br />
5 sm Ost<br />
30 sm Nord).<br />
Ermittle mithilfe der Maße in der Zeichnung die Geschwindigkeit der Bavaria in Knoten.<br />
f) Kommt es zum Zusammenstoß der beiden Schiffe, wenn sie jeweils ihren Kurs und ihre<br />
Geschwindigkeit beibehalten? Begründe.