Ãbungen zu den Lehrveranstaltungen 710.003 Computergrafik 1 ...
Ãbungen zu den Lehrveranstaltungen 710.003 Computergrafik 1 ...
Ãbungen zu den Lehrveranstaltungen 710.003 Computergrafik 1 ...
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
up<br />
cy<br />
y<br />
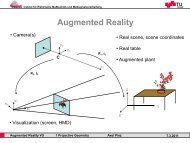
eye<br />
cx<br />
cz<br />
z<br />
lookat<br />
Abbildung 23: Kameramodell<br />
x<br />
Man beachte dass in dieser Übung ein linkshändiges Koordinatensystem verwendet wird. Sind die Basisvektoren<br />
bestimmt ergibt sich die Viewmatrix nach:<br />
⎛<br />
⎞<br />
cx x cx y cx z −〈cx, eye〉<br />
View = ⎜cy x cy y cy z −〈cy, eye〉<br />
⎟<br />
⎝cz x cz y cz z −〈cz, eye〉 ⎠ (21)<br />
0 0 0 1<br />
Auf die Transformation in Kamerakoordinaten durch die Viewmatrix folgt die Transformation in <strong>den</strong><br />
Clipspace durch die Projectionmatrix. Die Projektion ist bestimmt durch die Kameraparameter fov, near<br />
und far sowie das Seitenverhältnis aspect = w h<br />
des Ausgabebildes (wobei w die Breite und h die Höhe<br />
bezeichnet):<br />
⎛<br />
⎞<br />
1<br />
0 0 0<br />
aspect·tan( fov<br />
2 )<br />
1<br />
Projection =<br />
0 0 0<br />
tan(<br />
⎜<br />
fov<br />
2 )<br />
far near·far ⎟<br />
(22)<br />
⎝ 0 0<br />
⎠<br />
far−near near−far<br />
0 0 1 0<br />
View- und Projectionmatrix können <strong>zu</strong> einer gemeinsamen Transformation konkateniert wer<strong>den</strong>:<br />
Transform = Projection · View (23)<br />
Um einen dreidimensionalen Punkt p = ( x y z ) T<br />
von Welt- in Bildschirmkoordinaten <strong>zu</strong> transformieren<br />
wen<strong>den</strong> wir einfach diese Gesamttransformation auf <strong>den</strong> Punkt an:<br />
⎛ ⎞<br />
⎛ ⎞<br />
x C<br />
x<br />
p C = ⎜y C<br />
⎟<br />
⎝ z C<br />
⎠ = Transform · ⎜y<br />
⎟<br />
⎝z⎠ (24)<br />
w C 1<br />
Durch anschließende Homogenisierung erhalten wir <strong>den</strong> Punkt p D<br />
⎛ ⎞ ⎛ ⎞<br />
x D<br />
p D = ⎝y D<br />
⎠ = 1 x C<br />
⎝y C<br />
⎠ (25)<br />
w<br />
z C D z C<br />
Dieser Punkt liegt nun in sogenannten normalisierten Gerätekoordinaten vor. Dabei handelt es sich um ein<br />
Koordinatensystem in dem der Punkt (−1, 1) der linken oberen Ecke und (1, −1) der rechten unteren Ecke<br />
des Ausgabebildes entspricht. Die z-Koordinate liegt für alle Punkte die sich zwischen der near und far<br />
23